Анализ СД на ПК

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

«БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТРАНСПОРТА»

Кафедра «Прикладная математика»

АНАЛИЗ СТАТИСТИЧЕСКИХ ДАННЫХ НА ПЕРСОНАЛЬНОМ КОМПЬЮТЕРЕ

Лабораторный практикум

Гомель 2006

0

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ УЧРЕЖДЕНИЕ ОБРАЗОВАНИЯ

«БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТРАНСПОРТА»

Кафедра «Прикладная математика»

АНАЛИЗ СТАТИСТИЧЕСКИХ ДАННЫХ НА ПЕРСОНАЛЬНОМ КОМПЬЮТЕРЕ

Лабораторный практикум

Под редакцией канд. физ.-мат. наук, доцента В. С. Серёгиной

Одобрено методическими комиссиями строительного факультета и ФБО

Гомель 2006

1

Лабораторная работа № 1

ПЕРВИЧНАЯ ОБРАБОТКА СТАТИСТИЧЕСКИХ ДАННЫХ

Цель работы: ознакомиться с основными понятиями математической статистики и методикой проведения первичного исследования статистических данных.

Задание: произвести первичную обработку полученных экспериментальных данных и сделать обоснованный вывод о свойствах изучаемой случайной величины.

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

1 Выборочный метод

Допустим, результаты изучаемого вероятностного эксперимента могут быть описаны с помощью некоторой случайной величины X. В математической статистике множество всех мыслимых наблюдений, которые могли бы быть зафиксированы при воспроизведении эксперимента, принято называть генеральной совокупностью и обозначать kX. Генеральную совокупность можно рассматривать как множество всех объектов, которые подвергаются исследованию. Число элементов, образующих множество kX, называется

объемом генеральной совокупности.

Как правило, в большинстве практических задач, подвергнуть обследованию всю генеральную совокупность не представляется возможным (например, объем kX может быть бесконечным, исследование может оказаться слишком дорогостоящим или приводит к разрушению объекта изучения). Поэтому для исследования свойств случайной величины X чаще всего используется в ы б о р о ч н ы й м е т о д . Сущность этого метода состоит в том, что из рассматриваемой генеральной совокупности случайным образом извлекается часть объектов, называемая выборкой, которая и подвергается детальному изучению. Число n наблюдений, образующих выборку, называют объемом выборки. Затем, используя известные теоретико-вероятностные соотношения, по результатам выборочного обследования формулируются выводы о свойствах всей генеральной совокупности.

мощью на основании ограниченного числа выборочных данных получить как можно более полное представление об изучаемых случайных величинах.

Для того, чтобы по имеющейся выборке можно было сделать обоснованный вывод о свойствах всей генеральной совокупности, она должна быть р е п р е з е н т а т и в н о й (п р е д с т а в и т е л ь н о й ), т. е. хорошо отображать свойства исследуемой генеральной совокупности. Доказано, что для

4

получения представительной выборки выбор каждого элемента из генеральной совокупности должен осуществляться независимо от выбора остальных элементов и с сохранением принципа случайности. Кроме того, большое значение имеет объем исследуемой выборки.

2 Сгруппированный и интервальный статистические ряды

Итак, пусть для исследования свойств случайной величины (с.в.) X получена выборка объема n {x1, x2,…, xn}.

Последовательность выборочных значений х1, х2,…, хn, записанных в порядке их появления, представляет собой исходный статистический материал и называется простым статистическим рядом.

Для компактного, удобного и наглядного представления имеющихся статистических данных необходимо произвести их п е р в и ч н у ю о б р а - б о т к у .

Запишем все элементы выборки в порядке неубывания и обозначим члены такой последовательности x(i) , i = 1, 2, ..., n : x(1) ≤ x(2) ≤ ... ≤ x(n) , где

x(1) = min{x1, x2 ,..., xn}, x(n) = max{x1, x2 ,..., xn}.

Каждый элемент x(i) называется порядковой статистикой (вариантой), а последовательность

x(1) , x(2) ,..., x(n)

называется вариационным рядом, соответствующим имеющейся выборке. Если изучается дискретная случайная величина, число возможных зна-

чений которой не велико (n < 10), то для каждого из отличающихся друг от

и относительные частоты (частости) mi/n появления этих значений в выборке. Результаты вычислений заносятся в таблицу 1, которая называется

сгруппированным статистическим рядом.

Если изучается непрерывная случайная величина либо дискретная слу-

5

чайная величина, число возможных значений которой достаточно велико (n > 10), то диапазон [xmin(n); xmax(n)] всех наблюденных значений разбивается на k разрядов длины h, и подсчитываются числа выборочных данных, попавших в каждый из разрядов. Результаты расчетов заносятся в таблицу 2, которая называется интервальным статистическим рядом.

Таблица 2 – Интервальный статистический ряд

Для определения границ интервалов [Ci; Ci+1) можно воспользоваться

следующей методикой:

1 Вычислить размах варьирования выборочных значений: R = xmax – xmin, где xmin и xmax соответственно минимальное и максимальное значения вариационного ряда.

2 Определить длину шага разбиения h = R , где k – число разрядов раз- k

биения. Для примерной ориентации в выборе значения k можно воспользоваться формулой Стерджесса: k ≈ 1+ 3,322lg n ( 5 ≤ k ≤15 ), где n – объем

выборки. Выбор количества разрядов существенно зависит от объема выборки n. При больших n величину R, полученную по формуле Стерджесса, следует воспринимать как оценку снизу для R (для упрощения последующих расчетов полученное значение h может быть округлено в бóльшую или меньшую сторону).

3 Определить границы интервалов разбиения: C1 = xmin – h/2, C2 = C1 + h, C3 = C2 + h, и т. д. Процесс разбиения продолжается до тех пор, пока максимальный элемент выборки не попадет в интервал. Среднее значение каждого частичного интервала можно определить как среднее арифметическое его границ.

Элементы выборки, попавшие на границы разрядов разбиения, могут быть приписаны к какому-то одному из этих интервалов (например, к правому, как это сделано в таблице 2), либо частоты этих значений могут быть разделены поровну между двумя соседними интервалами.

Для графического представления сгруппированного статистического ряда обычно используется столбцовая диаграмма (рисунок 1), которая пред-

6

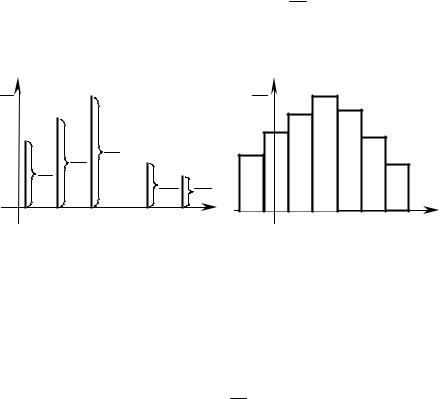
ставляет собой последовательность вертикальных отрезков длины mi/n, от-

ложенных от оси абсцисс в точках с координатами ~ . xi

Для графического изображения интервального статистического ряда чаще всего используется гистограмма относительных частот (рисунок 2). При построении гистограммы на оси абсцисс необходимо отложить границы

интервалов выборочных значений [Ci,; Ci+1) ( i =1, k ) и на каждом из этих

интервалов, как на основании, построить прямоугольники, площади которых равны mi/n, тогда высоты прямоугольников равны mi/(nhi). Площадь всей гистограммы, очевидно, равна 1.

3 Эмпирическая функция распределения

Эмпирической функцией распределения Fˆ(x) называется функция, ко-

торая каждому значению x ставит в соответствие относительную частоту события {X < x} (обозначающего тот факт, что с.в. Х примет значение мень-

шее, чем х). Расчетная формула для вычисления Fˆ(x) имеет вид:

Fˆ(x) = nx , n

где n – объём исследуемой выборки;

nx – число элементов выборки, меньших данного фиксированного зна-

чения х.

Свойства эмпирической функции распределения:

1 Все возможные значения эмпирической функции распределения принадлежат отрезку [0, 1]: 0 ≤ Fˆ(x) ≤ 1.

2 Fˆ(x) – неубывающая функция своего аргумента, то есть Fˆ(x1) ≤ Fˆ(x2)

7

для любых значений x1 и x2, таких, что x1 < x2 .

3 Если все выборочные значения исследуемой случайной величины при-

Важнейшее свойство эмпирической функции распределения состоит в том, что при увеличении объема выборки n, значение этой функции в каждой точке приближается к значению теоретической функции распределения F(x) в указанной точке, т. е. эмпирическая функция распределения является экспериментальным аналогом (оценкой) неизвестной исследователю теоретической функции распределения.

4 Оценки числовых характеристик

Важнейшим этапом статистической обработки данных является вычисление оценок числовых характеристик исследуемой случайной величины. Полученные оценки позволяют в числовой форме описать характерные черты статистического распределения и являются базой для построения математической модели изучаемого случайного явления.

Любая функция f (x1, x2 , ..., xn ) от результатов наблюдения x1, x2 , ..., xn исследуемой с. в. X называется выборочной статистикой или

просто статистикой. Статистика ˆ , используемая в качестве приближён-

Θ

ного значения неизвестного параметра Θ, называется статистической

оценкой параметра Θ.

Существует два вида оценок параметров: точечные и интервальные. То-

чечные оценки определяют точку ˆ , являющуюся некоторым приближени-

Θ

ем оцениваемого параметра Θ. Интервальная оценка представляет собой

гались как можно ближе к истинному значению оцениваемого параметра Θ.

смещённость и эффективность.

8

Статистическая оценка ˆ называется состоятельной, если ее вычис-

Θ

ляемое по опытным данным значение при увеличении объема выборки схо-

Оценка ˆ называется несмещенной (или оценкой без систематиче-

Θ

ской ошибки), если ее математическое ожидание совпадает со значением ˆ

Θ

оцениваемого параметра: M ˆ . [Θ] = Θ

Несмещенная оценка ˆ называется эффективной, если по сравнению с

Θ

другими оценками параметра, вычисляемыми на основании выборок одинакового объема n, она обладает наименьшей дисперсией.

Ниже приведены формулы для вычисления точечных оценок случайной величины на основании имеющихся выборочных данных x1, x2 , ..., xn .

1 В качестве оценки математического ожидания (характеризующего среднее значение случайной величины) используется среднее арифметиче-

величины сгруппированного статистического ряда, которому соответствует наибольшее значение частоты. По интервальному статистическому ряду определяется модальный интервал, в который попало наибольшее число элементов выборки, и в качестве точечной оценки моды может использоваться середина этого интервала.

3 Для определения выборочного значения медианы (средневероятного значения с. в.) используется вариационный ряд. В качестве оценки медианы xˆmed принимают средний член этого ряда, если значение n – нечётно, и сред-

нее арифметическое двух средних членов этого ряда, если n – чётно.

4 В качестве оценки дисперсии (являющейся мерой рассеивания значений случайной величины относительно ее среднего значения) используется статистика

9