
Анализ СД на ПК
.pdf
6) как только Z1 и Z2 |
найдены, двойное неравенство |
ˆ |
|
Z1 < Z(θ, θ) < Z2 |
|||
|
|
ˆ |
ˆ |
решается относительно θ и получается искомый интервал θ1 < θ < θ2 . |
|||
|
f(Z) |
|
|
Площадь = α/2 |
|
Площадь = α/2 |
|
|
1 – α |
||
|
|
|
|
Z1 |
|
Z2 |
|
Рисунок 1 – Двусторонняя критическая область статистического критерия |
|||
3 Доверительные интервалы для математического ожидания и дисперсии случайной величины, имеющей нормальное распределение
Пусть вероятностный эксперимент описывается случайной величиной X и известно, что X подчиняется нормальному закону распределения вероятностей
|
|
1 |
|
− |
(x−a)2 |
|
|
f (x) = |
|
|
e 2σ2 , σ > 0, a R, x R , |
||||
|
|
|
|
||||
σ |
|
2π |
|||||
|
|
|
|
|
|
||
где σ – среднее квадратическое отклонение случайной величины X, причем значения a и σ нам неизвестны;
a – математическое ожидание.
Построим доверительный интервал (aˆ1; aˆ2 ) для неизвестного значения
a математического ожидания. Воспользуемся алгоритмом, изложенным в пункте 2:
1) извлечем выборку {x1, x2 ,..., xn} объема n из генеральной совокупно-
сти;
2) по выборке найдем точечные оценки параметров a и σ :
|
|
|
1 |
n |
1 |
|
n |
|||
aˆ = |
|
= |
∑xi , σˆ 2 = |
|
∑(xi − |
|
)2 ; |
|||
x |
x |
|||||||||
n |
n −1 |
|||||||||
|
|
|
i=1 |
i=1 |
||||||
|
|
|
|
|
|
|||||
3) составим случайную величину
|
|
|
− |
a |
. |
|
t = |
|
x |
(2) |
|||
|
|
|
|
|||
|
σˆ / n |
|
||||
Доказано, что случайная величина t имеет распределение Стьюдента с
20
ν = n −1 степенями свободы; |
|
|
|
||
|
4) зададим доверительную вероятность P = (1− α) ; |
|
|
||
|
5) найдем t1 и t2 такие, что |
|
|
|
|
|
|
t2 |
|
|
|
|
|
P{t1 < t < t2 }= ∫ ft (x)dx = 1− α , |
|
|
(3) |
|
|
t1 |
|
|
|
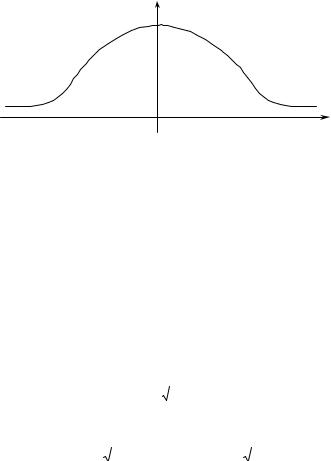
где |
ft (x) |
– плотность распределения Стьюдента, график которой изображен |
|||
|
|
на рисунке 2. |
|
|
|
|
|
f(t) |
|
|
|
|
|
t1 = – t(α/2; n – 1) |
t2 |
= t(α/2; n – 1) |
t |
|
|
|
|
|
|
|
|
Рисунок 2 – Плотность распределения Стьюдента |
|
||
Поскольку кривая плотности распределения Стьюдента симметрична относительно вертикальной оси, мы можем выражение (3) записать так
t(α / 2; n−1)
2 ∫ f (x)dx = 1− α ,
0
пользуясь таблицей значений t-распределения (приложение Б), найдем зна- чение t(α / 2; n−1) ;
6) полагая известными значения t1 = −t(α / 2; n−1) и t2 = t(α / 2; n−1) , запишем из (3) выражение в скобках
{− t(α / 2; n−1) |
< t < t(α / 2; n−1) }= (подставим выражение для t из (2)) = |
|
||||||||||||||||||
|
|
|
|
|
|
− a |
|
|
|
|
|
|
||||||||
|
|
|
|
x |
|
|
|
|
|
|||||||||||
|
|
= − t(α / 2; n−1) < |
|
|
|
|
|
|
|
|
< t(α / 2; n−1) |
. |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
σˆ / n −1 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
Решим двойное неравенство относительно a: |
|
|
|
|||||||||||||||||
|
|
− t(α / 2; n−1) |
|
σˆ |
< a < |
|
+ t(α / 2; n−1) |
|
σˆ |
|
|
|||||||||
|
x |
|
|
|
x |
|
|
|
. |
(4) |
||||||||||
|
|
|
|
|
|
|||||||||||||||
n −1 |
n −1 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Таким образом, мы построили доверительный интервал (4) для параметра a.
21

Для построения интервальной оценки (σˆ 12 ; σˆ 22 ) неизвестной дисперсии
σ2 |
воспользуемся тем, что случайная величина |
(n −1)σˆ |
2 |
подчинена χ2 - |
|||||||||||
|
|
|
|||||||||||||
|
σ2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
распределению с (n – 1) степенями свободы. Поэтому |
|
|
|||||||||||||
|
|
χ(21−α / 2; n−1) < |
(n −1)σˆ |
2 |
< χ(2α / 2; n−1) , |
(5) |
|||||||||
|
|
|
|
|
|
||||||||||
|
|
σ2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где |
χ(21−α / 2; n−1) |
– (1− α / 2) |
– процентная точка |
χ2 -распределения с (n – 1) |
|||||||||||
|
|
степенями свободы; |
|
|
|
|
|
|
|
|
|
||||
|
χ(2α / 2; n−1) |
– α / 2 – процентная |
точка χ2 -распределения с (n – 1) сте- |
||||||||||||
|
|
пенями |
свободы (приложение В). Разрешая неравенство |
||||||||||||
|
|
(5) относительно σ2 , получим случайный доверительный |
|||||||||||||
|
|
интервал для неизвестного параметра σ2 |
|||||||||||||
|
|
|
(n −1)σˆ 2 |
|
|
|
(n −1)σˆ |
2 |
|
|
|
|
|||
|
|
|
|
|
< σ2 |
< |
|
|
|
|
|
. |
(6) |
||
|
|
|
|
|
χ(21−α / 2; n−1) |
|
|||||||||
|
|
|
χ(2α / 2; n−1) |
|
|
|
|
|
|
||||||
Соответственно доверительный интервал (σˆ 1 ; σˆ 2 ) для среднего квадратического отклонения имеет вид
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ 2 |
|
|
|
ˆ 2 |
|
|
|
|||
|
(n −1)σ |
|
< σ < |
(n −1)σ |
|
|
, |
(7) |
|||
|
|
|
|
|
|
||||||
χ(2α / 2; n−1) |
χ(12 −α / 2; n−1) |
||||||||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
и таким образом мы построили доверительный интервал для параметра σ .
Замечание – Если случайная величина X имеет произвольную функцию распределения f (x) , по формулам (4) и (7) можно строить приближенные доверительные интервалы соответственно для математического ожидания и среднего квадратического отклонения, если объем выборки достаточно велик, n ≥ 50 .
Пример 1 Из многочисленного коллектива работников фирмы случайным образом отобрано n = 25 работников. Средняя заработная плата этих работников составила x = 700 д.е. при выборочном среднеквадратическом отклонении σˆ = 100 д.е. Требуется с доверительной вероятностью P = 0,95 определить интервальную оценку:
а) для средней месячной заработной платы на фирме; б) суммы затрат фирмы на заработную плату отдела, состоящего из 520
сотрудников.
22

Р е ш е н и е . 1) Среднемесячная заработная плата на фирме характеризуется генеральной средней a. Требуется найти интервальную оценку (aˆ1; aˆ2 ) параметра a с доверительной вероятностью P = 0,95 . Согласно (4) имеем
|
|
|
|
|
σˆ |
|
|
a |
x |
± t |
|
|
|
|
, |
(α / 2; n−1) |
|
||||||
|
n −1 |
|
|
||||
|
|
|
|
|
|||
где t(α / 2; n−1) – α / 2 -процентная |
точка |
t -распределения (распределения |
|||
Стьюдента). По таблице (см. приложение Б) распределения |
|||||
Стьюдента находим t(0,025; 24) = 2,064 . Поэтому |
|||||
|
|
|
100 |
|
|
a |
700 |
± 2,064 |
|
|
. |
|
|
|
24 |
|
|
|
|
|
|
||
Таким |
образом, с |
вероятностью |
P = 0,95 |
можно гарантировать, что |
средняя |
заработная |
плата на |
фирме |
находится в пределах: |
{657,88 д.е. < a < 742,12 д.е.}. |
|
|
||
2) Средняя сумма затрат фирмы на заработную плату отдела из N сотрудников составит N a д.е. Следовательно, с вероятностью P = 0,95 можно утверждать, что затраты фирмы на заработную плату отдела не выйдут за пределы интервала:
{520 657,88 < N a < 520 742,12},
{342098 д.е. < N a < 385902 д.е.}.
Пример 2 При анализе точности фасовочного автомата было проведено n = 24 контрольных взвешиваний пятисотграммовых пачек кофе. По результатам измерений рассчитано выборочное среднее квадратическое отклонение σˆ = 0,8 г. Требуется с доверительной вероятностью P = 0,95 оценить
точность фасовочного автомата, то есть определить интервальную оценку σ. Р е ш е н и е . Согласно (6) интервальная оценка дисперсии
(n −1)σˆ |
2 |
< σ2 < |
(n −1)σˆ |
2 |
. |
|
|
|
|
||
|
|
|
|
||
χ(2α / 2; n−1) |
χ(21−α / 2; n−1) |
||||
По таблице процентных точек χ2 -распределения (см. приложение В) найдем
23

χ(2α / 2; n−1) = χ(20,025; 23) = 38,0757 ;
χ(21−α / 2; n−1) = χ(20,975; 23) = 11,6885 .
Следовательно,
σ2 |
23 0,64 |
|
23 0,64 |
|
|
|
|
; |
|
. |
|
|
|
||||
|
|
38,0757 |
|
11,6885 |
|
|
|
|
|
||
Значит с доверительной вероятностью P = 0,95 можно утверждать, что
истинное значение среднего квадратического отклонения σ будет находиться в интервале
0,622 г < σ < 1,122 г.
Предположив, что ошибка фасовочного автомата есть нормально распределенная случайная величина с нулевой средней и среднеквадратическим отклонением σ, можно с вероятностью 0,954 утверждать, что вес пачек кофе будет в пределах
(500 − 2σ; 500 + 2σ) = (500 − 2,244; 500 + 2,244) = (497,756; 502,244) .
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1 В лабораторной работе № 1 вы выполнили обработку статистических данных и вычислили точечную оценку x среднего значения исследуемой случайной величины X и точечную оценку σˆ среднего квадратического отклонения X. Перепишите из лабораторной работы № 1 значения величин n, x и σˆ .
2 |
Постройте вручную интервальные оценки для неизвестных истинных |
значений M[X ] и σ[X ]. |
|
3 |
Вычислите интервальные оценки для M[X ] и σ[X ] на ЭВМ (приложе- |
ние А, п. 6). |
|
4 |
Сделайте вывод. |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1 Что такое точечная и интервальная оценки параметров?
2 Почему возникает необходимость построения интервальной оценки параметра?
3 Что называется доверительной вероятностью?
4 Дайте определение доверительного интервала.
5 Что такое точность вычисления интервальной оценки?
24
Лабораторная работа № 3
ПОДБОР ЗАКОНА РАСПРЕДЕЛЕНИЯ ОДНОМЕРНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Цель работы: изучить методику применения критерия χ2 Пирсона для
проверки гипотезы о виде закона распределения случайной величины.
Задание: с помощью критерия χ2 проверить согласование выдвинутой
гипотезы о виде закона распределения исследуемой случайной величины с имеющимися выборочными данными.
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
1 Введение
При проведении статистического исследования экспериментальных данных часто возникает задача подбора закона распределения изучаемой случайной величины X. Например, рассмотрим работу счетчика импульсов ионизирующего излучения. Если случайная величина, характеризующая число зарегистрированных импульсов ионизирующего излучения, будет распределена по закону Пуассона, то счетчик находится в рабочем состоянии. Если же случайная величина будет распределяться по иному закону распределения, то счетчик считается неисправным.
Предположим, что согласно методике, описанной в лабораторной работе № 1, произведена первичная обработка имеющихся статистических данных. Дальнейшая задача, рассматриваемая в данной лабораторной работе, заключается в статистической проверке гипотез о виде функции распределения случайной величины.
2 Основные понятия статистической проверки гипотез
Статистическая гипотеза называется параметрической, если в ней сформулированы предположения относительно значений параметров функции распределения известного вида. Если в формулировке гипотезы не встречаются предположения о значениях параметров функции распределения, то такая гипотеза называется непараметрической.
Нулевой гипотезой называют выдвинутую гипотезу и обозначают H0 .
Альтернативной называется гипотеза, конкурирующая с нулевой гипотезой в том смысле, что если отвергается нулевая гипотеза, то принимается альтернативная. Ее обозначают Ha.
Суждения относительно истинности (ложности) статистических гипотез формулируются на основании выборки объема n с помощью статистических критериев.
Статистическим критерием называется вспомогательная случайная
25
величина К, с помощью которой принимается решение о принятии либо отклонении нулевой гипотезы.
При проверке статистических гипотез по выборочным данным всегда существует возможность принятия ложного решения. Это объясняется тем, что объем выборки конечен, и поэтому нельзя точно определить ни вид функции распределения, ни значения параметров.
Ошибкой первого рода называется ошибка отклонения верной нулевой гипотезы H0 .
Уровнем значимости α статистического критерия называется вероятность совершения ошибки первого рода.
Ошибкой второго рода называется ошибка принятия ложной нулевой гипотезы H0 .
Мощностью M статистического критерия К называется вероятность несовершения ошибки второго рода, т. е. M = 1 – β.
Будем рассматривать только один вид статистических критериев – статистические критерии значимости. Это значит, что будет заранее фиксироваться вероятность совершения ошибки первого рода (уровень значимости α) и тогда нет необходимости в нахождении ошибки второго рода β. Например, если при отклонении нулевой гипотезы H0 на уровне значимости
α = 0,05 мы совершаем ошибку первого рода ( считаем правильную нулевую гипотезу H0 ложной ), то в среднем ошибаемся в 5 из 100 случаев применения данного статистического критерия значимости.
3 Применение критерия Пирсона χ2 для проверки гипотезы о виде закона распределения случайной величины
Гипотеза о виде закона распределения изучаемой случайной величины обычно выдвигается на основании графического изображения статистического закона распределения, сведений о механизме формирования значений этой величины, а также на основании значений оценок числовых характеристик.
В таблицах 1 и 2 приведены сведения о наиболее часто используемых при решении практических задач законах распределения дискретных и непрерывных случайных величин. В графе «Примечание» этих таблиц приведены примеры случайных величин, подчиняющихся указанным законам, либо описан механизм формирования значений этих величин.
Если изучается непрерывная случайная величина, то вид гистограммы относительных частот обычно значительно облегчает задачу выдвижения гипотезы H0. Например, по виду гистограммы, изображённой на рисунке 1, а, логично выдвинуть гипотезу о равномерном законе распределения исследуемой случайной величины. Вид гистограмм, приведённых на рисунках 1, б и 1, в, напоминает соответственно кривые экспоненциального и нормального законов распределения. Большое внимание при выдвижении гипотез уделяется и вычисленным значениям числовых характеристик (примеры 1, 2).
26

27
Таблица 1 – Основные сведения о наиболее часто встречающихся на практике законах распределения дискретных случайных величин
Назва- |
|
|
|
Числовые характери- |
|
|
|
ние |
Возможные |
Пара- |
|
|
стики |
Вероятности возможных зна- |
|
закона |
Параметры |
|
|
Примечание |
|||
распре- |
значения |
метры |
|
M[X] |
D[X] σ[X] |
чений, столбцовая диаграмма |
|
|
|
|
|
|
|||
деления |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P(X = k) = Cnk pk qn−k |
|
Случайная величина X ха- |
||
|
|
|
|
|
|
|
|
|
|
рактеризует число появлений |
|||
|
|
|
|
|
|
|
|
pi |
|
|
|
|
|
Бино- |
X = 0, 1, 2, . |
|
|
|
|
|
|
|
|
|
|
события A в серии из n неза- |
|
p, n |
p = M[X ]/ n |
|
|
npq |
|
|
|
|
|||||
миаль- |
|
np |
npq |
|
|
|
|
висимых испытаний, в каж- |
|||||
|
.., n |
|
ˆ |
ˆ |
ˆ |
|
|
|
|
|
|
||
ный |
|
|
|
|
|
|
|
|
|
|
|
дом из которых это событие |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
0 |
np |
|
n |
xi |
может осуществиться с веро- |
|
|
|
|
|
|
|
|
|
ятностью p |
||||
|
|
|
|
|
|
|
|
|
P(X = k) = a |
k |
e−a |
|
Пример: число событий |
|
|
|
|
|
|
|
|
|
|
|
простейшего потока, харак- |
||
|
|
|
|
|
|
|
|
|
k! |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
теризующегося интенсивно- |
||
Пуас- |
X = 0, 1, |
|
|
|
|
|
|
pi |
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
стью a, где a – число собы- |
|||
a |
|
ˆ |
a |
a |
a |
|
|
|
|
||||
|
|
|
|
|
|
|
|||||||
сона |
2, ..., m, ... |
|
a = M[X ] |
|
|
|
|
тий, произошедших в тече- |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ние единицы времени |
|
|
|
|
|
|
|
|
0 |
a |
|
|
xi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Случайная величина X ха- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рактеризует число независи- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P(X = k) = qk p |
|
мых испытаний, произведён- |
|||||||||||
Гео- |
|
|
|
|
|
|
q |
|
|
|
pi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ных до первого появления |
|
метри- |
X = 0, 1, |
p |
ˆ |
ˆ |
1 |
− 1 |
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
события A, которое в каждом |
|||
2, ..., m, ... |
p = 1/(M[X ] + 1) |
p |
|
p |
2 |
|
p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
из этих испытаний может |
|||||
ческий |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
произойти с вероятностью p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi (при этом испытание, в кото- |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ром появляется событие A, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
не учитывается) |
0
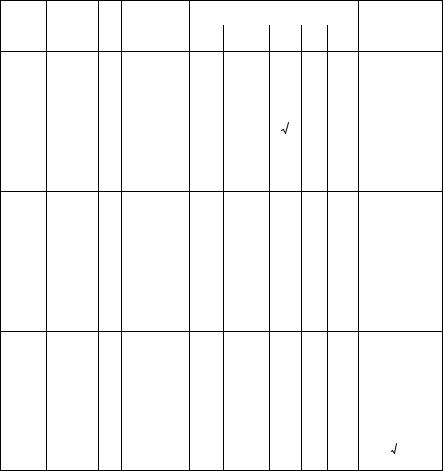
Таблица 2 – Основные сведения о наиболее часто встречающихся на практике
Закон распределения
Равномерный
Экспоненциальный (показательный)
Нормальный
Возможные
значения
X [a;b]
X [0;∞)
X R
Параметры
a b
λ
m
σ
Статистическая |
|
|
Числовые характеристики |
|
Вероятность |
||||||||||
|
|
|
попадания |
||||||||||||
|
|
оценка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
значений с. в. |
|
|
параметров |
|
|
|
M[X] |
|
D[X] |
|
σ[X] |
A[X] |
Ex[X] |
||||
|
|
|
|
|
|
в отрезок [α; β] |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aˆ = xmin − |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
xmax − xmin |
, |
|
|
|
|
|
b − a |
|
|
P(α ≤ X ≤ β) = |
||||
|
n −1 |
|
a + b (b − a)2 |
|
0 |
–1,2 |
|||||||||
|
|
|
|
|
|
= β − α |
|||||||||
|
bˆ = xmax + |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
2 |
|
|
2 3 |
|
||||||||
|
|
|
12 |
|
|||||||||||
|
|
xmax − xmin |
|
|
|
|
|
|
|
|
|
|
|
|
b − a |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
n −1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
ˆ |
1 |
1 |
1 |
|
P(α ≤ X ≤ β) = |
||||
λ = 1/ |
M[X ] |
λ |
|
λ2 |
|
λ |
2 |
6 |
−λα − e |
−λβ |
|
|
|
|
|
= e |
|||||
|
|
|
|
|
|
|
P(α ≤ X ≤ β) = |
|||||||
|
|
|
|
|
|
|
β − m |
|
− |
|||||
|
|
|
|
|
|
|
= Φ |
|
σ |
|
|
|||
mˆ |
ˆ |
|
|
|
|
|
|
|
|
|
|
|
||
= M[X ] |
m |
σ2 |
σ |
0 |
0 |
|
α − m |
|
||||||
σˆ |
= σˆ[X ] |
|
|
|
|
|
− Φ |
|
|
|
|
|||
|
|
|
|
|
|
σ |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
1 |
x |
|
t2 |
|
|
|
|
|
|
|
|
Φ(x) = |
|
∫e− |
|
dt |
|||
|
|
|
|
|
|
|
|
|
2 |
|||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
2π |
|||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проверка гипотезы о предполагаемом распределении производится с помощью непараметрических критериев значимости. Одной из групп таких критериев значимости являются критерии согласия, с помощью которых проверяются нулевые гипотезы о виде функции распределения случайной величины.
Одним из наиболее широко используемых на практике критериев согласия является критерий χ2 Пирсона. Он может использоваться для проверки гипотез о виде закона распределения как дискретных, так и непрерывных случайных величин.
28
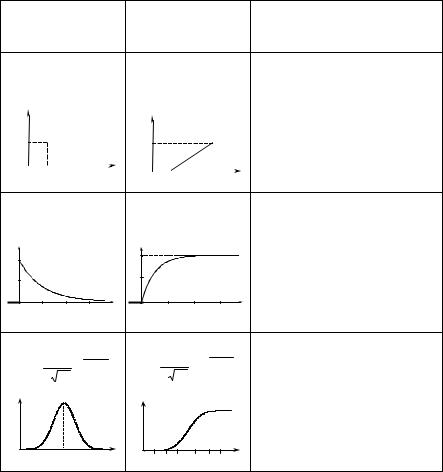
законах распределения непрерывных случайных величин
Функция плотности распределения Функция распределения Примечание вероятностей
|
|
|
|
1 |
|
|
|
|
|
|
|
0, |
|
x ≤ a; |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
x − a |
|
|
|
|
Если все возможные значения непре- |
||||||
|
|
|
|
|
|
|
, |
x [a;b]; |
|
|
|
|
|
|
|||||||
f (x) = b |
− a |
|
|
|
|
|
F(x) |
= |
|
|
, a < x ≤ b; |
рывной случайной величины принадле- |
|||||||||
|
x [a;b] |
|
− a |
||||||||||||||||||
|
|
|
0, |
|
|
|
|
b |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
x > b |
|
|
жат отрезку [a; b], и все значения, попа- |
||||
|
|
f(x) |
|
|
|
|
|
|
|
F(x) |
|
|
|
|
|
|
|
дающие на этот отрезок равновозмож- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ны, то данная случайная величина X |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
распределена по равномерному закону. |
||||
|
|
b−a |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример: величина погрешности при |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
округлении данных |
|
|
|
0 а |
|
|
b |
x |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
0 |
а |
|
b |
x |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
f (x) = |
0, |
|
x < 0; |
|
0, |
|
|
x < 0; |
Примеры: |
|
|
|
|
|||||
|
−λx |
, x ≥ 0 |
|
F(x) = |
− e |
−λx |
, |
x ≥ 0 |
|
– промежуток |
времени |
между |
мо- |
|||||
|
|
λe |
|
|
|
1 |
|
|
ментами |
наступления двух |
|
последова- |
||||||
f(x) |
|
|
|
|
|
F(x) |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
тельных событий простейшего потока; |
|||||||
λ |
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
– разнообразные временные характе- |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ристики |
функционирования |
техниче- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
ских устройств (время безотказной ра- |
|||||
0 |
1 |
|
2 |
3 |
x |
0 |
1 |
|
2 |
|
3 |
x |
боты оборудования и т. д.) |
|
|
|
||
|
1 |
e− |
(x−m)2 |
|
|
1 |
x |
− |
(t−m)2 |
|
Если случайная |
величина X пред- |
||
f (x) = |
2σ2 |
, |
F(x) = |
∫e |
2σ2 |
dt, ставляет собой сумму большого числа |
||||||||
σ |
2π |
|
|
|
σ |
2π |
−∞ |
|
|
|
независимых |
(или |
слабо |
зависимых) |
x R |
|
|
|
|
x R |
|
|
|
|
|
случайных величин, |
сопоставимых по |
||
f(x) |
|
|
|
|
F(x) |
|
|
|
|
|
уровню своего влияния на суммарный |
|||
|
|
|
|
|
1 |
|
|
|
|
|
результат, то эта величина имеет рас- |
|||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
0,5 |
|
|
|
|
|
пределение, близкое к нормальному |
|||
|
|
|
|
|
|
|
|
|
|
Пример: реальные значения пара- |
||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
m |
|
|
x |
|
m |
|
|
|
x |
метров изготовленного изделия |
|||
Применение критерия χ2 основано на сопоставлении эмпирических mi и теоретических npi (вычисленных в предположении справедливости проверяемой гипотезы) частот попадания значений исследуемой случайной величины в рассматриваемые частичные разряды. В качестве меры расхождения эмпирического и теоретического распределений используется статистика
|
k |
(m |
i |
− np |
i |
)2 |
|
|
χ2 |
= ∑ |
|
|
|
, |
(1) |
||
|
|
npi |
|
|
||||
|
i=1 |
|
|
|
|
|
|
29
