
Анализ СД на ПК
.pdf
которая при n → ∞ независимо от вида предполагаемого распределения стремится к распределению χ2 с ν = k − r −1 степенями свободы (здесь k – число разрядов разбиения, r – число параметров теоретического распределения, оцениваемых по выборке).
Легко заметить, что при незначительных отклонениях значений mi от npi значение критерия χ2 будет близким к нулю. И наоборот, большое значение критерия χ2 свидетельствует о существенном отклонении значений mi и npi.
а) mi 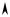
nhi |
|
|
|
|
С1 |
С2 |
С3 |
… Сk–1 Сk Сk+1 |
x |
б) |
mi |
|
|
|
|
в) |
mi |
|
|
|
|
|
nhi |
|
|
|
|
|
nhi |
|
|
|
|
|
С1 |
С2 |
С2 |
… Сk–1 Сk |
Сk+1 x |
|
С1 |
С2 |
С3 |
… Сk–1 Сk |
Сk+1 x |
Рисунок 1 – Примеры гистограмм относительных частот
Необходимыми условиями применения критерия χ2 являются достаточно большой объем выборки (n ≥ 30) и отсутствие в теоретическом распределении разрядов с небольшим (npi < 5) числом наблюдений. Для обеспечения последнего условия интервалы, для которых npi < 5, необходимо объединить с соседними. На хвостах распределения допускается значение npi ≥ 1.
4 Алгоритм применения критерия χ2 для проверки гипотезы о виде закона распределения исследуемой случайной величины
1 Строится статистический закон распределения случайной величины.
2 Выбирается уровень значимости α.
3 Формулируется гипотеза о виде закона распределения исследуемой случайной величины.
4 Вычисляются теоретические вероятности pi попадания значений случайной величины Х в рассматриваемые разряды разбиения: pi = P(Ci ≤ X < Ci+1 ) = F(Ci+1 ) − F(Ci ) , ( i = 1, 2,..., k ), где F(x) – гипотетическая функция распределения случайной величины X.
30
Замечание – Если изучается непрерывная случайная величина, то при вычислении значений pi необходимо изменить границы первого и последнего частичных
интервалов разбиения таким образом, чтобы учесть все возможные значения, которые может принять случайная величина предполагаемого класса. В зависимости от конкретного вида проверяемой гипотезы границы частичных интервалов необходимо изменить следующим образом:
Вид закона распределения |
Первый интервал |
Последний интервал |
|
разбиения |
разбиения |
||
|
|||
|
|
|
|
Равномерный |
[aˆ; C2 ) |
[Ck ; bˆ) |
|
|
|
|
|
Экспоненциальный |
[0; C2 ) |
[Ck ; ∞) |
|
|
|
|
|
Нормальный |
(−∞; C2 ) |
[Ck ; ∞) |
|
|
|
|
Для того чтобы |
избежать ошибок при вычислении вероятностей |
pi = P(Ci ≤ X < Ci+1 ) |
непрерывной случайной величины удобно воспользо- |
ваться расчетными таблицами 3–5. |
|
Таблица 3 – Вычисление вероятностей |
pi равномерно распределенной случай- |
|||||||||
ной величины |
|
|
|
|
|
|
|
|
|
|
C |
i |
P |
= |
Ci+1 − Ci |
|
|||||
|
|
|
|
|
||||||
|
i |
|
|
|
|
bˆ − aˆ |
||||
|
|
|
|
|
|
|
||||
|
ˆ |
P1 = |
|
C2 − C1 |
||||||
|
|
|
|
|
|
|||||
C1 = a |
|
bˆ − aˆ |
||||||||
|
|
|
|
|
|
|
||||
C |
2 |
P |
= |
|
C3 − C2 |
|
||||
|
|
|||||||||
|
2 |
|
|
|
|
bˆ − aˆ |
||||
|
|
|
|
|
|
|
||||
C |
3 |
P = |
C4 − C3 |
|
||||||
|
||||||||||
|
3 |
|
|
|
|
bˆ − aˆ |
||||
|
|
|
|
|
|
|
||||
… |
|
|
|
|
|
… |
||||
|
|
|
|
|
|
|
||||
Ck+1 = bˆ |
|
|
|
|
|
––– |
||||
|
|
|
∑Pi =1 |
|||||||
|
|
|
i |
|
|
|
|
|
||
31
Таблица 4 – Вычисление |
вероятностей |
|
pi |
|
показательно |
распределенной |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
случайной величины |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ci |
|
|
|
|
|
|
|
|
|
|
|
|
|
Zi = e−λCi |
|
|
|
|
Pi = Zi − Zi+1 |
|
|
|
|
||||||||||||||
|
|
C = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
P = Z |
|
− Z |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z1 = e |
−λC1 |
|
|
|
|
1 |
2 |
|
|
|
|
|
|||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
P |
= Z |
|
− Z |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Z2 = e |
−λC2 |
|
|
|
|
2 |
3 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
P = Z |
|
− Z |
|
|
|
|
|
|
||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Z3 = e |
−λC3 |
|
|
|
|
3 |
4 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|||||||||
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
|
|
|||||
|
Ck+1 = ∞ |
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
ˆ |
|
|
|
|
|
––– |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
k+1 |
= e−λ ∞ = 0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑Pi |
= 1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
Таблица 5 – Вычисление |
вероятностей |
|
pi |
|
случайной величины, |
|
имеющей |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
нормальное распределение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
Ci |
|
|
|
|
|
Zi |
= |
|
|
Ci − mˆ |
|
|
|
|
|
|
Ф(Zi ) |
Pi = Ф(Zi+1) − Ф(Zi ) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C = −∞ |
|
|
|
Z |
1 |
= |
|
C1 − mˆ |
|
= −∞ |
|
Ф(Z |
1 |
) = Ф(−∞) = −0,5 |
P = Ф(Z |
2 |
) − Ф(Z |
1 |
) |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
σˆ |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
C |
2 |
|
|
|
|
|
|
|
Z |
2 |
|
= |
|
C2 − mˆ |
|
|
|
|
Ф(Z |
2 |
) = ... * |
P |
= Ф(Z |
3 |
) − Ф(Z |
2 |
) |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σˆ |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
C |
3 |
|
|
|
|
|
|
|
Z |
1 |
|
= |
C3 − mˆ |
|
|
|
|
|
Ф(Z |
3 |
) = ...* |
P |
= Ф(Z |
3 |
) − Ф(Z |
2 |
) |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σˆ |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
… |
|
|
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
|
|
|
|
|
|
|
… |
|
|
|
… |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Ck+1 = +∞ |
Z |
k+1 |
= |
|
Ck+1 − mˆ |
= +∞ |
|
Ф(Zk+1 ) = Ф(+∞) = 0,5 |
|
|
|
––– |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑Pi = 1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
* Ф(Z1) , Ф(Z2 ) , Ф(Z3) , …, Ф(Zk+1) вычисляются по таблице значений функции |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
x |
|
− |
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Φ(x) = |
|
∫e |
2 dt (приложение Г). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 Определяются значения теоретических частот npi (i = 1, 2,…, k). При необходимости для обеспечения условия npi ≥ 5 объединяются несколько соседних разрядов разбиения.
6 Вычисляется выборочное значение критерия χ2 по формуле (1).
32
7 По таблице критических точек распределения χ2 определяется критическое значение χα2 ,ν , соответствующее заданному уровню значимости α и
числу степеней свободы ν = k – r– 1.
Если расчётное значение критерия попадает в критическую область, т. е. χˆ 2 > χα2 ,ν , то проверяемая гипотеза отвергается (при этом вероятность отклонения верной нулевой гипотезы равна α).
В случаях, когда наблюденное значение χˆ 2 не превышает критического
χˆ 2 ≤ χα2 ,ν , считают, что выдвинутая гипотеза не противоречит опытным
данным. Подчеркнем, что полученный результат свидетельствует лишь о приемлемом согласовании проверяемой гипотезы с имеющимися выборочными данными и в общем случае не является доказательством истинности этой гипотезы.
Пример 1 На основании выборочных данных, приведённых в примере 1 лабораторной работы № 1, подобрать закон распределения случайной величины X, характеризующей число отказов оборудования, произошедших в течение рабочей смены. Уровень значимости α принять равным 0,05.
Решение. После проведения первичной обработки полученных данных (см. пример 1 лабораторной работы № 1), опираясь на сведения о механизме формирования значений исследуемой случайной величины (поток отказов оборудования обычно обладает свойствами простейшего потока), учитывая вид построенной столбцовой диаграммы и значения оценок числовых харак-
теристик Mˆ [X ] = 2, Dˆ[X ] = 1,92 , то есть Mˆ [X ] ≈ Dˆ[X ], выдвигаем гипотезу
о том, что изучаемая случайная величина подчиняется закону распределения Пуассона:
|
|
|
ai |
|
|
−a |
____ |
H |
0 |
: P(X = i) = |
|
|
e |
|
, i = 1, ∞ ; |
i ! |
|
||||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
ai |
|
|
−a |
____ |
H |
a |
: P(X = i) ≠ |
|
|
e |
|
, i = 1, ∞ . |
i ! |
|
|
|||||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Для проверки этой гипотезы с помощью критерия χ2 выполним следующие действия.
Вычислим оценку параметра a распределения Пуассона: aˆ = Mˆ [X ] = 2 . Вычислим вероятности наблюденных значений изучаемой случайной
величины:
p = P(X = i) = |
ai |
e−a (i = 0, 1, 2,…, 6, …); |
|
|
|||
i |
i |
! |
|
|
|
||
33

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
6 |
a |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
pi |
|
= P(X > 6) = 1− ∑ pi |
= 1− ∑ |
|
e−a |
(i = 7); |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i=0 |
|
|
i=0 |
i! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
P(X = 0) = |
|
20 |
|
e |
−2 |
= e |
−2 |
= 0,1353 ; |
P(X = 1) = |
|
21 |
e |
−2 |
= 2e |
−2 |
|
= 0,27067 ; |
||||||||||||||||||||||||
0! |
|
|
|
|
|
1! |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
P(X = 2) = |
22 |
|
e |
−2 |
= |
2e |
−2 |
= 0,27067 |
; |
|
P(X = 3) = |
23 |
|
e |
−2 |
= |
4 |
e |
−2 |
= 0,1804 ; |
|||||||||||||||||||||
|
2! |
|
|
|
|
|
|
|
3! |
|
|
|
3 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
P(X = 4) = |
|
2 |
4 |
|
e |
−2 |
= |
|
2 |
|
e |
−2 |
= 0,0902 |
; |
P(X = 5) = |
25 |
|
e |
−2 |
= |
|
4 |
|
e |
−2 |
= 0,036 ; |
|||||||||||||||
|
4! |
|
|
3 |
|
|
|
5! |
|
|
|
15 |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
P(X = 6) = 26 e−2 = 4 e−2 = 0,012 ; 6! 45
P(X > 6) = 1− (0,1353+ 0,27067 + 0,27067 + 0,1804 + 0,0902 + 0,036 + 0,012 =
= 1 – 0,9948 = 0,0052. Заполним расчётную таблицу:
~ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
>6 |
x |
||||||||
mi |
4 |
19 |
12 |
6 |
7 |
1 |
1 |
0 |
pi |
0,1353 |
0,27067 |
0,27067 |
0,1804 |
0,0902 |
0,036 |
0,012 |
0,0052 |
npi |
6,765 |
13,5335 |
13,5335 |
9,02 |
4,51 |
1,8 |
0,6 |
0,26 |
Учитывая, что теоретические частоты наблюденных значений, находящихся в трех последних столбцах таблицы, не превышают трех единиц, при вычислении значения критерия χ2 эти разряды объединим в один:
|
|
6 |
(mi |
− npi ) |
2 |
|
|
(4 |
− 6,765) |
2 |
|
|
(19 −13,5335) |
2 |
|
(12 −13,5335) |
2 |
|
|||||
χˆ 2 |
= ∑ |
|
= |
|
+ |
|
+ |
|
+ |
||||||||||||||
|
|
i=1 |
np |
i |
|
|
|
|
|
6,765 |
|
|
|
|
13,5335 |
|
13,5335 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
+ |
(6 − 9,02) |
2 |
+ |
|
(7 − 4,51)2 |
|
+ |
(2 − 2,66)2 |
= 6,062. |
|
|
||||||||||
|
|
|
9,02 |
|
4,51 |
|
|
|
2,66 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
По таблицам квантилей распределения χ2 определим критическое значе- |
|||||||||||||||||||||||
ние χα2 |
,ν , соответствующее α = 0,05, ν = k – r – 1 = 6 – 1 – 1 = 4: χ02,05;4 = 9,488. |
||||||||||||||||||||||
Поскольку |
выборочное |
|
значение |
|
критерия |
|
меньше критического |
||||||||||||||||
χˆ 2 ≤ χα2 |
,ν , можно сделать вывод о том, что гипотеза не противоречит экспе- |
||||||||||||||||||||||
34
риментальным данным; поэтому нет оснований для отклонения проверяемой гипотезы.
Пример 2 На основании опытных данных, приведённых в примере 2 лабораторной работы № 1, подобрать закон распределения непрерывной случайной величины X, характеризующей время безотказной работы оборудования между двумя последовательными переналадками. Уровень значимости
αпринять равным 0,05.
Ре ш е н и е . Используя результаты первичной обработки выборочных данных (вид полученной гистограммы и значения оценок числовых характе-
ристик: Mˆ [X ] = 8,98174 ≈ σˆ[X ] = 8,34 ), а также учитывая сведения о физи-
ческом смысле полученных значений, выдвигаем гипотезу о том, что случайная величина X распределена по экспоненциальному закону:
H0 : f (x) = λe−λx , λ > 0, x ≥ 0,
Ha : f (x) ≠ λe−λx , λ > 0, x ≥ 0 .
Проверим согласование сформулированной гипотезы H0 с эксперимен-
тальными данными с помощью критерия χ2.
Вычислим оценку параметра экспоненциального закона распределения:
ˆ |
1 |
|
1 |
|
λ = |
|
= |
|
≈ 0,1113 . |
ˆ |
8,98174 |
|||
|
M[X ] |
|
|
При вычислении вероятностей pi = P(Ci ≤ X < Ci+1) изменим границы первого и последнего интервалов разбиения в соответствии с замечанием, приведенным на странице 34.
Ci |
Zi = e |
− 0,1113 Ci |
Pi = Zi − Zi+1 |
|
|||
0 |
|
1 |
0,2828 |
|
|
|
|
2,987 |
0,7172 |
0,3124 |
|
|
|
|
|
8,127 |
0,4047 |
0,1763 |
|
|
|
|
|
13,267 |
0,2284 |
0,0995 |
|
|
|
|
|
18,407 |
0,1289 |
0,0562 |
|
|
|
|
|
23,547 |
0,0727 |
0,0317 |
|
|
|
|
|
28,687 |
0,0410 |
0,0179 |
|
|
|
|
|
33,827 |
0,0232 |
0,0232 |
|
|
|
|
|
∞ |
|
0 |
––– |
|
|
|
∑Pi = 1 |
|
|
|
i |
35
Определим значения теоретических частот и занесём их в расчётную таблицу:
[Ci; Ci+1) |
[0; 2,987) |
[2,987; |
[8,127; |
[13,267; |
[18,407; |
[23,547; |
[28,687; |
[33,827; ∞) |
8,127) |
13,267) |
18,407) |
23,547) |
28,687) |
33,827) |
|||
|
|
|
|
|
|
|
|
|
mi |
14 |
16 |
9 |
4 |
3 |
2 |
1 |
1 |
pi |
0,2828 |
0,3124 |
0,1763 |
0,0995 |
0,0562 |
0,0317 |
0,0179 |
0,0232 |
|
|
|
|
|
|
|
|
|
npi |
14,140 |
15,620 |
8,815 |
4,975 |
2,810 |
1,585 |
0,895 |
1,160 |
Поскольку значения npi, соответствующие четырем последним интервалам разбиения, не превышают пяти единиц, объединим эти интервалы в один и для вычисления значения критерия χ2 составим следующую расчётную таблицу:
[Ci; Ci+1) |
|
[0; 2,987) |
[2,987; 8,127) |
|
[8,127; 13,267) |
[13,267; 18,407 ) |
|
[18,407; ∞) |
||||||||||
mi |
|
14 |
16 |
|
|
|
9 |
|
|
|
4 |
|
|
|
7 |
|
||
pi |
|
0,2828 |
0,3124 |
|
|
0,1763 |
|
0,0995 |
|
|
0,1290 |
|||||||
npi |
|
14,140 |
15,620 |
|
|
8,815 |
|
|
4,975 |
|
|
6,450 |
||||||
Вычислим значение критерия χ2: |
|
|
|
|
|
|
|
|
||||||||||
χ2 |
= |
(14 −14,140)2 |
+ |
(16 −15,620)2 |
|
+ |
(9 − 8,815)2 |
+ |
(4 − 4,975)2 |
+ |
||||||||
|
|
14,140 |
|
|
|
15,620 |
|
|
|
8,815 |
|
|
4,975 |
|
||||
|
|
|
|
+ |
(7 − 6,450)2 |
= 0,252. |
|
|
|
|
|
|||||||
|
|
|
|
|
6,450 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Критическое значение критерия, соответствующее значениям α = 0,05 и ν = k − r −1= 5 −1−1= 3, определим с помощью приложения В:
χα2 ,ν = χ02,05;3 = 7,82 .
Поскольку χ2 < χα2 ,ν , можно сделать вывод о том, что проверяемая ги-
потеза об экспоненциальном законе распределения изучаемой случайной величины Х не противоречит экспериментальным данным и нет основания для отклонения нулевой гипотезы.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1 Получить выборку значений исследуемой случайной величины X с указанным значением уровня значимости α и записать её на диск (см. приложение А, п. 2).
36
2 Произвести первичную обработку полученных статистических данных. 3 Выдвинуть гипотезу о виде закона распределения изучаемой случай-
ной величины.
4 Проверить согласование сформулированной гипотезы с имеющимися выборочными данными (ручной расчёт):
–вычислить оценки параметров предполагаемого закона распределе-
ния;
–если рассматривается дискретная случайная величина, то вычислить
вероятности всех возможных значений случайной величины
= ( = ~ ) . Если рассматривается непрерывная случайная величина, то pi P X xi
вычислить вероятности попадания значений случайной величины в i-й интервал pi = P(Ci ≤ X < Ci+1) , i = 1, 2, …, k;
–определить значения теоретических частот npi, i = 1, 2, …, k;
–вычислить выборочное значение критерия χ2;
–сравнить выборочное значение критерия с критическим значением
χα2 ,ν и сделать вывод.
5 Проверить согласование выдвинутой гипотезы с имеющимися экспериментальными данными с помощью ППП:
–вычислить выборочное значение критерия χ2 (приложение А, п. 9);
–построить совместное графическое изображение статистического и предполагаемого теоретического распределений изучаемой случайной величины (см. приложение А, п. 9).
6 Сделать вывод о законе распределения вероятностей изучаемой случайной величины.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1 Что такое непараметрическая гипотеза?
2 Что такое нулевая, альтернативная гипотезы?
3 Из каких соображений выдвигается гипотеза о виде закона распределения случайной величины?
4 Что такое статистический критерий?
5 Какие ошибки могут быть совершены при статистической проверке гипотез? 6 Что такое уровень значимости статистического критерия?
7 Что называется статистическим критерием значимости?
8 По какой формуле вычисляется критерий χ2?
9 Сформулируйте алгоритм применения критерия Пирсона.
10Как найти критическое значение критерия χ2 (α, ν) ?
11Как вычислить число степеней свободы ν ?
37
Лабораторная работа № 4
СТАТИСТИЧЕСКАЯ ПРОВЕРКА ПАРАМЕТРИЧЕСКИХ ГИПОТЕЗ
Цель работы: изучить основные понятия теории статистической проверки гипотез и проверки параметрических гипотез.
Задание: по заданным выборкам провести статистическую проверку:
–гипотез о равенстве математического ожидания некоторому фиксированному значению;
–гипотезы о равенстве математических ожиданий двух генеральных совокупностей.
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
1 Основные понятия
На практике часто решаются задачи сравнения технологических процессов по различным параметрам: производительности, экономичности, точности достижения определенной технической характеристики и т. д. На языке математической статистики такие задачи формулируются как задачи сравнения или статистической проверки гипотез относительно параметров распределения. Рассмотрим, например, случайную величину X – время пребывания вагона на сортировочной станции. Пусть с. в. X имеет функцию распределения F(x, θ), где θ – параметр распределения. Предположим, что с целью уменьшения времени простоя вагонов на станции введены усовершенствования в технологический процесс обработки составов. Если мы возьмем одну выборку наблюденных значений с. в. X, полученную до внесения изменений в технологический процесс, а другую – после изменений, и вычислим
ˆ |
ˆ |
параметра θ распределения F(x, θ), то они, |
две точечные оценки θ1 |
и θ2 |
очевидно, не будут равны между собой. Спрашивается, связано ли это с изменениями, внесенными в технологический процесс, либо разница в значениях оценок обусловлена случайными факторами?
Статистическая гипотеза называется непараметрической, если в ней сформулировано предположение о виде закона распределения исследуемой случайной величины.
Статистическая гипотеза называется параметрической, если в ней сформулированы предположения относительно значений параметров распределения.
Суждения относительно истинности (ложности) статистических гипотез формулируются на основании выборки объема n. Наряду с выдвинутой гипотезой будем рассматривать одну или несколько альтернативных (конкурирующих) гипотез.
38
Нулевой гипотезой называют выдвинутую гипотезу и обозначают H0 .
Обычно нулевые гипотезы утверждают, что различия между сравниваемыми величинами (параметрами или функциями распределения) отсутствуют, а наблюдаемые отклонения обусловлены случайными колебаниями выборки.
Альтернативной называется гипотеза, конкурирующая с нулевой гипотезой в том смысле, что если отвергается нулевая гипотеза, то принимается альтернативная. Ее обозначают Ha .
Пусть для решения задачи сравнения из нормальной N(a, σ) генеральной совокупности извлечена выборка {x1, x2 ,..., xn} объема n . Приведем примеры нулевых и альтернативных параметрических гипотез (таблица 1).
Таблица 1 – Примеры нулевых и альтернативных параметрических гипотез
Нулевые |
|
Альтернативные |
|
|
|
|
|
H0 : |
a = a0 |
Ha : |
a ≠ a0 , или a < a0 , или a > a0 |
|
|
|
|
H0 : |
σ = σ0 |
Ha : |
σ ≠ σ0 , или σ < σ0 , или σ > σ0 |
|
|
|
|
Статистическим критерием называется случайная величина R , с помощью которой принимается решение о принятии либо отклонении нулевой гипотезы. Для проверки статистических гипотез по критериям значимости необходимо знать условный закон распределения построенной случайной величины в предположении выполнения нулевой гипотезы.
При проверке статистических гипотез по выборочным данным всегда существует возможность принятия ложного решения. Это объясняется тем, что объем выборки конечен, и поэтому нельзя точно определить ни вид функции распределения, ни значения параметров.
Ошибкой первого рода называется ошибка отклонения верной нулевой гипотезы H0 .
Уровнем значимости α статистического критерия называется вероятность совершения ошибки первого рода.
Ошибкой второго рода называется принятие ложной нулевой гипотезы H0. Вероятность совершения ошибки второго рода принято обозначать буквой β.
Мощностью M статистического критерия R называется вероятность несовершения ошибки второго рода, т. е. M = 1 – β.
Будем рассматривать только один вид статистических критериев – статистические критерии значимости. Это значит, что будет заранее фиксироваться вероятность совершения ошибки первого рода (уровень значимости α). На фиксированном уровне значимости мы можем принять только одно из двух решений: «отклонить проверяемую нулевую гипотезу» или «результаты выборки не дают основания для отклонения нулевой гипотезы».
39
