Анализ СД на ПК

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский государственный университет транспорта

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

A[X ] = β1

(n −1)(n − 2) σˆ 3

.pdf

Скачиваний:

Добавлен:

22.02.2016

Размер:

1.18 Mб

Скачать

☆

<<< < Предыдущая 12 / 102 3 4 5 6 7 8 9 10 > Следующая >>>

			1	n
ˆ	2			∑		2
ˆ	2					2
D[X ] = σˆ		=			(xi − x)		.	(2)
D[X ] = σˆ		=	n −1		(xi − x)		.	(2)
				i=1

5 Оценка среднего квадратического отклонения

σˆ[X ] = σˆ =	ˆ	(3)
	D[X ] .

6 Оценка коэффициента асимметрии (представляющего собой меру «скошенности» распределения случайной величины относительно среднего значения)

∑(xi −

i=1

A[X ] = β1

(4)

∑

(x − x)2

i=1

В пакете статистических программ STATGRAPHICS для вычисления оценки коэффициента асимметрии используется формула

Для симметричных функций плотности распределений оценка ˆ долж-

β1

на быть близка к нулю, в то время как для распределения, гистограмма кото-

рого имеет «длинную часть», расположенную справа от ее вершины,

а если слева – то	ˆ	< 0 .
	β1

7 Оценка коэффициента эксцесса вычисляется по формуле

∑(xi −

i=1

E[X ]= β2

− 3 .

∑

−

i=1

ˆ	> 0 ,
β1

(5)

В пакете STATGRAPHICS оценка Eˆ[X ] вычисляется следующим образом:

n (n +1)∑(xi

−

− 3(n −1)

∑(xi

−

i=1

E[X ]= β2

(n −1)(n − 2)(n − 3)σˆ 4

Коэффициент эксцесса характеризует островершинность распределения (поведение кривой распределения в районе ее модального значения).

Напомним, что своеобразным аналогом отсчета в измерении степени островершинности служит нормальное распределение, для которого теоре-

ˆ	ˆ
тическое значение β2 = 0	( β2 – близка к нулю). Для островершинного (по
	ˆ	, а для плосковершинного –
сравнению с нормальным) распределения – β2 > 0		, а для плосковершинного –
ˆ
β2 < 0 .
		2	, σˆ	ˆ	ˆ
Замечание – Приведенные выше статистики x , σˆ		2		ˆ	ˆ
Замечание – Приведенные выше статистики x , σˆ				β1	, β2 являются состоя-
тельными и несмещенными оценками соответственно		M[X ] ,			D[X ] , σ[X ] , A[X ] и
E[X ] .

Пример 1 При изучении характеристик работы цеха в результате наблюдений получена выборка значений случайной величины X, число отказов оборудования в течение рабочей смены: 3, 1, 0, 1, 3, 6, 2, 2, 1, 1, 4, 4, 1, 4, 2, 0, 1, 5, 3, 2, 2, 1, 3, 1, 1, 4, 2, 1, 1, 3, 1, 2, 1, 0, 2, 1, 2, 0, 1, 1, 1, 4, 4, 2, 1, 4, 1, 2, 3, 2.

Задание: исследовать экспериментальные данные с целью изучения свойств случайной величины X.

Р е ш е н и е . 1 Построим вариационный ряд, соответствующий полученной выборке: 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 5, 6.

2 Поскольку изучаемая случайная величина является дискретной, ее статистический закон распределения запишем в виде сгруппированного статистического ряда:

~
i	x	0	1	2	3	4	5	6

mi		4	19	12	6	7	1	1
mi / n		0,08	0,38	0,24	0,12	0,14	0,02	0,02

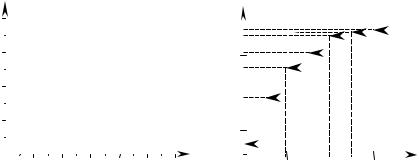
Столбцовая диаграмма, построенная на основании сгруппированного статистического ряда, изображена на рисунке 3.

3 Построим эмпирическую функцию распределения исследуемой случайной величины:

при x ≤ 0: Fˆ(x) = 0 , т. к. нет ни одного наблюденного значения с.в., меньшего 0;

при 0 < x ≤ 1 только одно значение случайной величины x = 0 меньше
				~
рассматриваемых значений			ˆ	равна относительной частоте
			х, поэтому F(x)
события {Х = 0};	ˆ	= 0,08	;
	F(x)
при 1 < x ≤ 2	ˆ	равна сумме относительных частот событий {Х = 0}
	F(x)

и {Х = 1}: Fˆ(x) = 0,08 + 0,38 = 0,46 ;

при 2 < x ≤ 3: Fˆ(x) = 0,08 + 0,38 + 0,24 = 0,7 и т.д. Таким образом:

										0		при			x ≤ 0;
														0 < x ≤1;
									0,08			при		0 < x ≤1;
									0,46			при	1 < x ≤ 2;
							ˆ		0,70			при	2 < x ≤ 3;
							F(x) =					при 3 < x ≤ 4;
									0,82			при 3 < x ≤ 4;
									0,96			при	4 < x ≤ 5;

									0,98 при 5 < x ≤ 6;
										1		при			x > 6.
										1		при			x > 6.
		График функции				ˆ	изображён на рисунке 4.
		График функции				F(x)	изображён на рисунке 4.
			mi									ˆ
0,4			n									F(x)
0,4			n									1
0,3

												0,8


0,2												0,6




0,1												0,4


												0,2




0		1		2	3	4	5	6 xi				0				1 2 3 4 5 6	x

	Рисунок 3 – Столбцовая диаграмма										Рисунок 4 – График эмпирической функ-
					(пример 1)							ции распределения (пример 1)

4 Вычислим точечные оценки числовых характеристик случайной величины X.

Оценка математического ожидания

M[X

] = x =

∑ximi =

n i=1

(0 4 +1 19 + 212 + 3 6 + 4 7 + 51+ 6 1) = 2 [отказа].

Оценка моды данной случайной величины равна 1 [отказ] ( xˆmod = 1), так

как этому значению соответствует наибольшее значение частоты.

Оценку медианы определим на основании вариационного ряда

xˆmed

x(25) + x(26)

2 + 2

= 2 [отказа].

Оценка дисперсии

∑

D[X ] = σˆ

(xi

− x)

mi =

((0 − 2)

4 + (1− 2)

19 + (2 − 2)

12 +

n −

i=1

+ (3 − 2)2 6 + (4 − 2)2 7 + (5 − 2)2 1+ (6 − 2)2 1) = 1,9184 [отказа2 ].

Оценка среднего квадратического отклонения

σˆ[X ] = Dˆ[X ] = 1,385 [отказа]. Оценки коэффициентов асимметрии и эксцесса:

n ∑(xi −

i=1

A[X

] = β1

= 0,816 ;

(n −1)(n − 2) σˆ 3

n (n +1)∑(xi

− 3(n −1)

− x)

∑(xi − x)

i=1

E[X ]= β2

= 0,179 .

−1)(n − 2)(n − 3)σˆ 4

Выводы. Итак, мы выполнили анализ выборки значений дискретной случайной величины, характеризующей число отказов оборудования в течение рабочей смены. Объём выборки n = 50. Минимальное число отказов оборудования в течение рабочей смены равно 0, максимальное – 6. Среднее значение числа отказов равно 2; наиболее вероятное – 1, а средневероятное – 2. Среднеквадратическое отклонение числа отказов оборудования от среднего значения равно 1,385.

Пример 2 В процессе функционирования технического устройства, его параметры могут выходить из области допустимых значений. В этом случае необходимо производить переналадку устройства. Исследуемая случайная величина Х представляет собой продолжительность безотказной работы устройства (выраженную в часах) между двумя последовательными переналадками:

6,421;	5,034;	0,599;	10,687; 26,294;		7,852;	14,040;	8,933;	4,062;	1,573;
5,455;	2,810;	15,658;	3,692;	1,825;	17,760;	8,030;	3,218;	2,872;	8,247;
0,417;	1,995;	0,611;	12,059;	0,665;	21,434;	22,102; 10,709;		2,283;	5,649;
6,773;	30,034;	3,702;	12,834;	2,723;	5,255;	12,595;	3,533;	34,540;	9,238;
1,673;	24,919; 15,511;		7,154;	1,816;	8,401;	22,239;	2,902;	3,083;	7,176.

Задание: произвести первичную обработку полученных опытных данных с целью изучения свойств случайной величины Х.

Р е ш е н и е . 1 Построим вариационный ряд:

0,417;	0,599;	0,61;	0,665;	1,573;	1,673;	1,816;	1,825;	1,995;	2,283;
2,723;	2,810;	2,872;	2,902;	3,083;	3,218;	3,533;	3,692;	3,703;	4,062;
4,176;	5,034;	5,255;	5,455;	5,649;	6,421;	6,773;	7,154;	7,852;	8,030;
8,247;	8,401;	8,933;	9,238;	10,687; 10,709; 12,059; 12,595; 12,834; 14,040;

15,511; 15,658; 17,760; 21,434; 22,102; 22,239; 24,919; 26,294; 30,034; 34,540.

Статистический закон распределения данной непрерывной случайной величины представим в виде интервального статистического ряда.

Вычислим длину интервала:

				h =			R	=		xmax − xmin			=	34,54 − 0,417		= 5,14 .
				h =			k	=	1+ 3,322 lg n				=	1+ 3,322 lg 50		= 5,14 .
							k		1+ 3,322 lg n					1+ 3,322 lg 50
Определив границы интервалов разбиения (C1 = xmin – h/2 = 0,417 – 2,57 =
= –2,153, C2 = C1 + h = –2,153 + 5,14 = 2,987,															C3 = C2 + h = 2,987 + 5,14 = 8,127
и т. д.), построим интервальный статистический ряд:

[C ; C	i+1	)	[–2,153;		[2,987;						[8,127;	[13,267;			[18,407;	[23,547;	[28,687;	[33,827;
i	i+1		2,987)		8,127)						13,267)	18,407)			23,547)	28,687)	33,827)	38,967)
			2,987)		8,127)						13,267)	18,407)			23,547)	28,687)	33,827)	38,967)

~			0,417		5,557						10,697	15,837			20,977	26,117	31,257	36,397
xi			0,417		5,557						10,697	15,837			20,977	26,117	31,257	36,397
mi			14			16					9		4		3	2	1	1
mi / n			0,28		0,32						0,18		0,08		0,06	0,04	0,02	0,02

Для контроля		убедимся,				что	mi
k	k						nh
∑mi = n = 50 , ∑mi / n =1.							0,06
∑mi = n = 50 , ∑mi / n =1.
i=1	i=1
Графическое изображение ин-							0,04
тервального статистического ряда
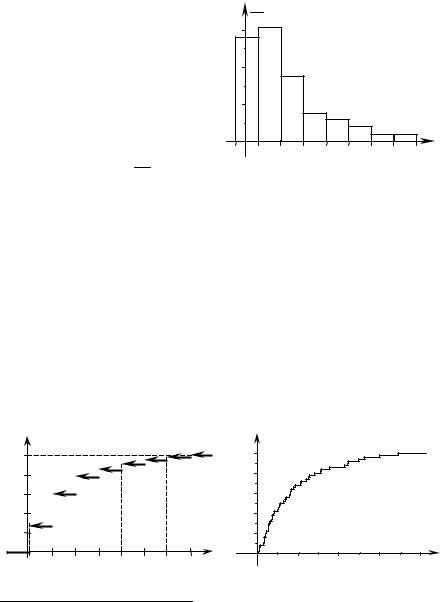
приведено на рисунке 5.							0,02
2 Для	приближённого					по-	0,02
2 Для	приближённого					по-
строения	эмпирической			функции
распределения воспользуемся						со-	–2,153 2,987	38,967 x
	ˆ	∑	mi *				–2,153 2,987	38,967 x
	ˆ		mi *		:		Рисунок 5 – Гистограмма относительных
отношением F[x] =				n	:		Рисунок 5 – Гистограмма относительных
		~		n				частот (пример 2)
		xi <x						частот (пример 2)

	0	при		x ≤ 0,417;
			0,417 < x ≤ 5,557;
	0,28	при	0,417 < x ≤ 5,557;
	0,6	при	5,557	< x ≤ 10,697;
	0,78	при	10,697	< x ≤15,837;
ˆ		при	15,837 < x ≤ 20,977;
F(x) = 0,86		при	15,837 < x ≤ 20,977;
	0,92	при	20,977 < x ≤ 26,117;
				< x ≤ 31,257;
	0,96	при	26,117	< x ≤ 31,257;
			31,257 < x ≤ 36,397;
	0,98	при	31,257 < x ≤ 36,397;
		при		x > 36,397.
	1	при		x > 36,397.

График полученной таким образом эмпирической функции распределения приведён на рисунке 6, а.

	а)			б)
ˆ				ˆ	(x)
F(x)				F	(x)
1				1,0
1
0,8				0,8
0,8
0,6				0,6
0,6
0,4				0,4
0,2				0,2
0,417	5,557 10,697	36,397	x	0	10	20	30	40	x

Рисунок 6 – График эмпирической функции распределения (пример 2)

* При использовании этой формулы принимаем допущение о том, что исследуемая случайная величина принимает только значения, соответствующие серединам интервалов [Ci; Ci+1) с частотами, равными mi (i =1, 2, …, k).

На рисунке 6, б приведён график эмпирической функции распределения данной случайной величины, построенный при использовании всего набора имеющихся экспериментальных данных.

Вычислим точечные оценки числовых характеристик случайной величины, обозначающей продолжительность безотказной работы устройства между двумя последовательными переналадками:

1 50

M[X ] =

∑ xi

= 8,92174 [ч];

n i=1

∑(xi

D[X ] = σˆ

− x)

69,322

[ч

];

n −

i=1

σˆ[X ] = σˆ = 8,326 [ч];

n ∑(xi

−

i=1

A[X ] = β1

= 1,36715 ;

(n −1)(n − 2) σˆ 3

n (n +1)∑

(xi − x)

−

∑(xi − x)

3(n −1)

i=1

E[X ]= β2

= 1,27 .

(n −1)(n −

2)(n − 3)σˆ 4

Вкачестве оценки моды можно принять среднее значение модального интервала [2,987; 8,127): xˆmod = 5,557 ч.

Вкачестве оценки медианы примем среднее значение между 25-м и 26-м элементами вариационного ряда: xˆmed = (5,649 + 6,421) / 2 = 6,035 ч.

Выводы. В результате исследования выборки значений непрерывной случайной величины, характеризующей время безотказной работы устройства между двумя последовательными переналадками, получили следующие результаты, ч: минимальное время безотказного функционирования – 0,417, максимальное – 34,54, среднее значение времени безотказного функционирования устройства – 8,922, наиболее вероятное значение – 5,557, средневероятное – 6,035. Среднеквадратическое отклонение времени безотказного функционирования устройства от среднего значения – 8,326. Оценка коэффициента асимметрии – 1,367, оценка коэффициента эксцесса – 1,27.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1 Изучить теоретические сведения.

2 Получить у преподавателя выборку значений случайной величины.

3 Произвести вручную первичную обработку статистических данных:

–построить вариационный ряд;

–построить сгруппированный или интервальный статистический ряд и его графическое изображение;

–вычислить эмпирическую функцию распределения и построить график этой функции;

–вычислить точечные оценки числовых характеристик изучаемой случайной величины.

4 Произвести первичную обработку полученной выборки с помощью ЭВМ:

–записать выборку на диск (приложение А, п. 2);

–вычислить оценки числовых характеристик (приложение А, п. 4);

–построить гистограмму частот исследуемой выборки (см. приложение А, п. 4).

5 Сравнить результаты, полученные при ручном расчёте и расчёте на ЭВМ.

6 Сделать вывод о свойствах изучаемой случайной величины.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1 Что называется случайной величиной? Какие типы случайных величин вы знаете?

2 Что называется генеральной совокупностью?

3 Что называется выборкой? Какими свойствами должна обладать выборка?

4 Для чего используется выборочный метод? Какая выборка называется репрезентативной? Укажите условия получения репрезентативных выборок.

5 Что называется вариационным рядом?

6 Укажите последовательность проведения первичной обработки статистических данных.

7 Опишите методику построения сгруппированного и интервального статистических рядов и их графического изображения.

8 Дайте определение эмпирической функции распределения и укажите ее свойства.

9 Что называется выборочной статистикой; статистической оценкой параметра? Что представляют собой точечные и интервальные оценки?

10 Какие требования предъявляются к статистическим оценкам?

11 Какие статистики используются в качестве точечных оценок основных числовых характеристик? Какими свойствами они обладают?

Лабораторная работа № 2

ПОСТРОЕНИЕ ИНТЕРВАЛЬНЫХ ОЦЕНОК ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ

Цель работы: изучить методику построения интервальных оценок параметров распределения вероятностей случайной величины.

Задание: построить интервальные оценки математического ожидания и дисперсии исследуемой случайной величины.

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

1 Основные понятия

Вычисляя на основании имеющихся у нас выборочных данных оценку

ˆ	, x2	,..., xn )	ˆ
θ (x1			параметра θ, мы понимаем, что величина θ является лишь

приближенным значением неизвестного параметра θ, даже в том случае, когда эта оценка состоятельна, несмещённа и эффективна. Поэтому возникает вопрос: как сильно отклоняется это приближенное значение от истинного?

Нельзя ли указать интервал вида ˆ1 ˆ 2 , который с заранее заданной веро- (θ , θ )

ятностью, близкой к единице, накрывает неизвестное нам истинное значение θ искомого параметра?

	Если	такой интервал мы сможем построить, то длина интервала
ˆ	ˆ	= ε , ε > 0 будет характеризовать точность вычисления оценки па-
ˆ	ˆ
θ1	− θ2

раметра θ: чем меньше величина ε , тем точнее оценка. Действительно, если

случайный интервал (θ1

; θ2 ) накрывает с заданной вероятностью истинное

значение параметра θ, то, принимая за оценку параметра θ значение θ1 (или

θ2 ), мы допустим ошибку не более, чем ε .

Доверительной вероятностью

оценки

называется

вероятность

P = (1− α)

выполнения

неравенства

< ε :

< ε}= 1− α ;

θ1

− θ2

θ1 −

θ2

. Выбор доверительной вероятности определяется конкретными

θ1

< θ < θ2

условиями; обычно используются значения 1− α , равные 0,90; 0,95; 0,99. Доверительная вероятность оценки показывает, что при извлечении дос-

таточно большого числа выборок объема n из одной и той же генеральной

совокупности с функцией распределения F(x, θ) в (1− α)100 %				случаях па-
	ˆ	ˆ	α 100% интерва-
раметр θ будет накрываться интервалом (θ1		; θ2 ) , и лишь	α 100% интерва-
ˆ	ˆ
лов (θ1	; θ2 ) не содержит оцениваемый параметр.
Доверительным интервалом называется интервал			ˆ	ˆ
Доверительным интервалом называется интервал			(θ1, θ2 ) , накры-

вающий неизвестный параметр θ с заданной доверительной вероятностью

P = (1− α) .
ˆ	ˆ
Мы говорим «Интервал (θ1	; θ2 ) будет накрывать неизвестное истин-
	ˆ	и	ˆ	вычисляются по
ное значение параметра θ» потому, что значение θ1		и	θ2	вычисляются по

выборке и поэтому случайны и изменяют свои значения от выборки к вы-

борке, а значение параметра θ остается неизменным.
	Иногда удается построить доверительный интервал, границы которого
			ˆ				ˆ	ˆ
симметричны относительно точечной оценки θ				параметра θ : θ1				= θ − ε ;
ˆ	ˆ	ˆ	ˆ	P{	ˆ	< ε}= 1	− α .

θ2	= θ + ε . И тогда	P(θ − ε < θ	< θ + ε)= 1− α или		θ − θ

2 Схема построения доверительных интервалов

Методика построения доверительных интервалов для параметра θ распределения вероятностей:

1)из генеральной совокупности значений случайной величины X, имеющей функцию распределения F(x, θ), извлекается выборка объема n;

ˆθ

2)по результатам выборки находится точечная оценка θ параметра распределения вероятностей;

3) составляется вспомогательная случайная величина Z Z ˆ , закон

= (θ, θ)

распределения вероятностей f (Z) которой известен; 4) задается доверительная вероятность (1− α) ;

5) используя плотность распределения вероятностей f (Z) случайной величины Z, находят такие два числа Z1 и Z2 (рисунок 1), что

ˆ				Z2
ˆ			}= ∫ f (Z)dZ = 1− α ;				(1)
P{Z1 < Z(θ, θ) < Z2			}= ∫ f (Z)dZ = 1− α ;				(1)
				Z1
ˆ	}=	α	;	ˆ	}=	α	;
P{Z(θ, θ) < Z1	}=	2	;	P{Z(θ, θ) > Z2	}=	2	;
		2				2

<<< < Предыдущая 12 / 102 3 4 5 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.02.201634.3 Кб10А4_40.doc
#
22.02.20167.16 Mб729АВТОПОГРУЗЧИКИ_МЕТОДИЧКА.doc
#
21.11.2019836.1 Кб15Альбом по усилению жб элементов.doc
#
22.02.201663.49 Кб12Алюминиевые сплавы.doc
#
26.04.201918.68 Mб52Анализ СД на ПК.doc
#
22.02.20161.18 Mб28Анализ СД на ПК.pdf
#
22.02.2016345.09 Кб32Англ.язык.doc
#
22.02.20161.25 Mб264Английский язык.doc
#
12.11.201981.92 Кб12АНЕМИЯ ВСЛЕДСТВИЕ КРОВОПОТЕРИ.doc
#
30.08.2019240.64 Кб16анкуд, 123 вопросы.doc
#
22.02.2016184.61 Кб123АП №2.docx