2 Регрессионный анализ

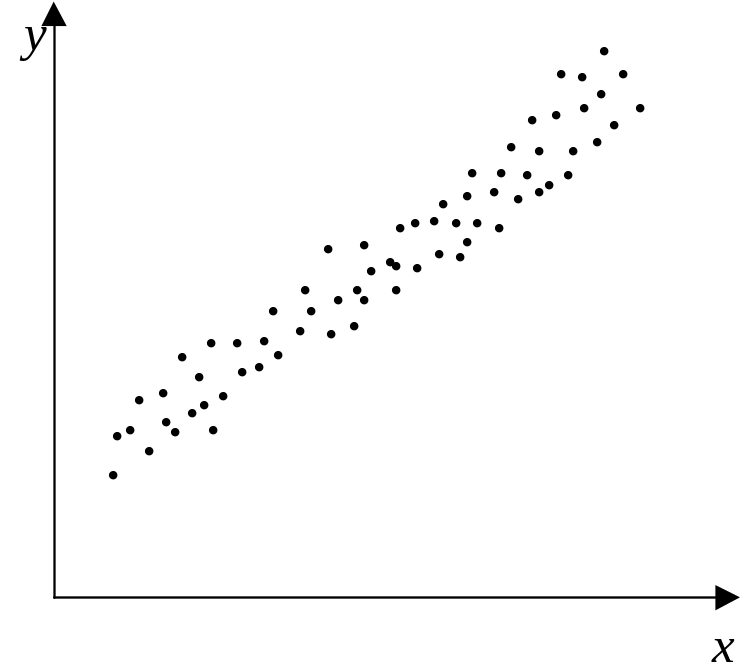
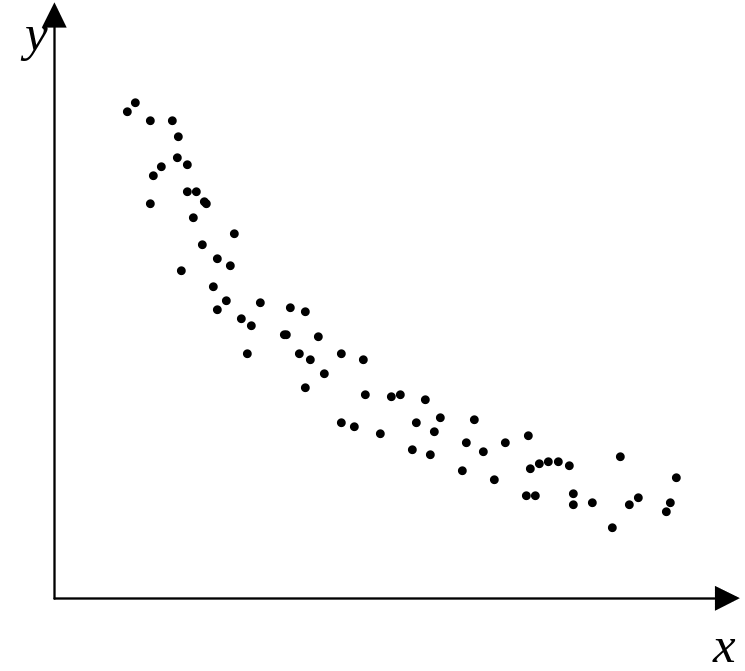
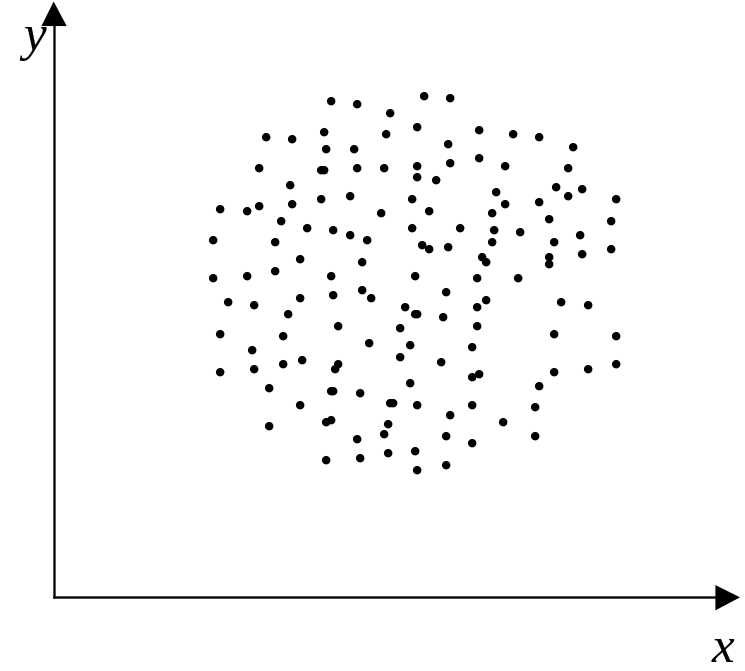
Пусть дана выборка значений двумерной с. в. (X,Y)={(x₁, y₁), (x₂, y₂) … (x_n, y_n)}, где n – объем двумерной выборки. Первым шагом в построении эмпирического уравнения регрессии между с. в. является графическое отображение значений двумерной с. в. в виде точек (x₁, y₁), ..., (x_n, y_n) на плоскости X-Y, называемое диаграммой рассеяния (корреляционным полем) (рисунок 2).

а)		б)
в)		г)
Рисунок 2 – Диаграмма рассеяния, соответствующая линейной (а), экспоненциальной (б), параболической (в) регрессионной зависимости и отсутствию регрессионной зависимости (г)

Визуальный анализ диаграммы рассеяния и предметная постановка задачи (физический смысл рассматриваемых величин) позволяет сделать предположение о виде уравнения регрессии. Если предполагается, что зависимость между с. в. X и Y линейна (рисунок 2, а), то теоретическая модель регрессионной зависимости между с. в. задается уравнением (1) – теоретической моделью линейной регрессии Y на X:

M[Y | X = x] = _ + _ x, (1)

т. е. для каждого Х = х_i имеется условное распределение с. в. Y со средним значением (_ + _ x_i). Таким образом, для каждого i-го наблюдения справедлива следующая зависимость:

 = ₀ + ₁x_i + e_i, , (2)

где у_i – i-е выборочное значение с. в. Y;

₀ – параметр линейной регрессии, требующий определения;

₁ – параметр линейной регрессии, требующий определения;

х_i  – i-е выборочное значение с. в. Х;

e_i  – ошибка, вызванная отклонением i-го наблюдения с. в. Y от условного среднего М[Y | X = х_i]. Ошибки e_i обусловливаются упрощением вида зависимости Y от X (без учёта всех влияющих факторов), а также возможной ошибкой в выборе формы регрессии (в действительности она может описываться другим уравнением).

3 Метод наименьших квадратов

Для оценивания параметров уравнения регрессии _ , _ ,… наиболее часто применяется метод наименьших квадратов (МНК). Идею МНК продемонстрируем на примере определения параметров линейной регрессионной зависимости вида (1).

Рассмотрим функцию S(_ , _ ,…), равную сумме квадратов отклонений выборочных значений y_i случайной величины Y от значения , предсказанного уравнением регрессии в точке X = x_i (рисунок 3):

. (3)

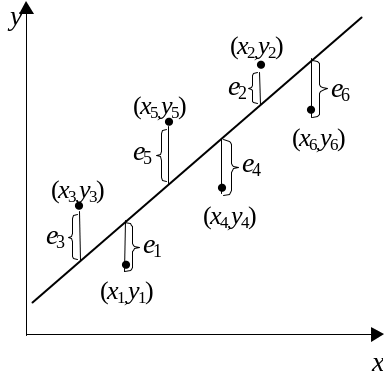
Фактически эти отклонения в каждой точке x_i равны e_i .

Рисунок 3 – Отклонения наблюденных значений зависимой случайной величины Y от значений, предсказываемых уравнением регрессии

Для случая линейной регрессии оценки параметров ₀ и _ получаются минимизацией по ₀ и _ суммы квадратов отклонений e_i выборочных значений с. в. Y от значений, предсказываемых уравнением регрессии Y на X, т. е. минимизацией функции

.

Из курса математического анализа известно, что для нахождения минимума функции S(_, _) необходимо приравнять к нулю частные производные этой функции S (по неизвестным _ и _) и решить полученную систему уравнений, называемых нормальными:

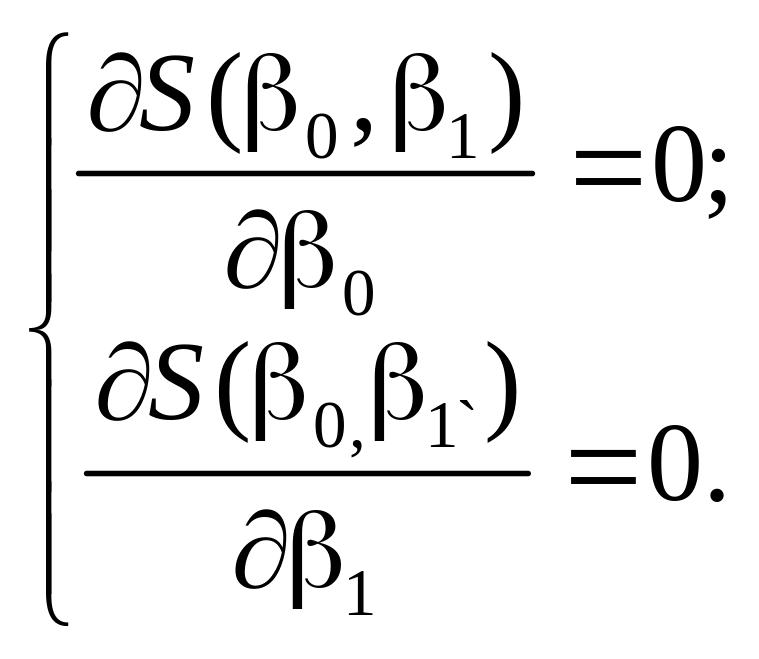(4)

Система уравнений (4) имеет единственное решение, если определитель матрицы ее коэффициентов не равен нулю. Полученные значения и , являющиеся решением системы (4), называются оценками параметров регрессии. Для предполагаемой линейной регрессионной зависимости (2) оценки минимизируют ошибку, возникающую при аппроксимации выборки прямой, и вычисляются по формулам:

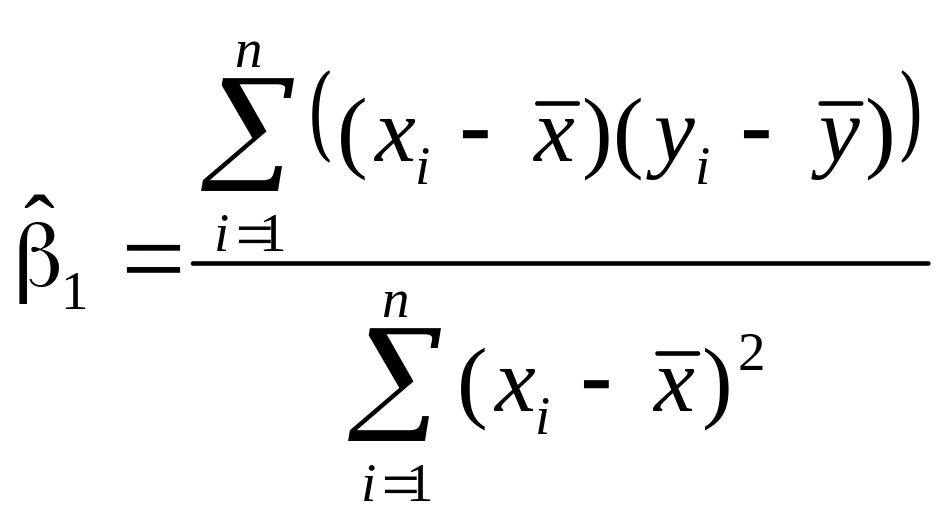; ; (5)

; . (6)

В результате оценка уравнения линейной регрессии (эмпирическое уравнение линейной регрессии, прямая, полученная МНК) будет иметь вид: .

В предположении, что значения ошибок {e₁, e₂,…, e_n}, возникающих при аппроксимации выборки уравнением линейной регрессии, являются взаимно независимыми случайными величинами с нормальным распределением, нулевым математическим ожиданием и постоянной дисперсией, оценки параметров таких уравнений регрессии (полученные МНК) являются несмещенными, состоятельными и эффективными.

Метод наименьших квадратов применим для оценивания параметров уравнений регрессии произвольного вида (гиперболической, параболической, экспоненциальной, логарифмической и т. д.).