6 Проверка значимости оценок коэффициентов корреляции и детерминации

Оценки коэффициентов корреляции и детерминации сами являются случайными величинами, так как для различных выборок из одной и той же генеральной совокупности могут принимать различные значения. При малых объемах выборок эти различия будут особенно существенными. Поэтому при нахождении оценок коэффициентов корреляции и детерминации используется проверка значимости этих оценок, которая позволяет сделать вывод о существенности описания действительной зависимости выбранным уравнением регрессии.

Фактически, проверка значимости оценки коэффициента корреляции/детерминации заключается в статистической проверке параметрической гипотезы о том, что действительное значение коэффициента равно нулю (r = 0 или R² = 0), а отличие от нуля соответствующей оценки ( или ) вызвано лишь случайностью выборки.

Проверка значимости . Чтобы сделать статистический вывод о значимости оценки коэффициента корреляции (при проверке линейной регрессионной зависимости) выдвигается нулевая гипотеза об отсутствии линейной зависимости между исследуемыми с. в. (т. е. H₀: r = 0; H_a: r  0). Если гипотеза H₀ отклоняется, то считается, что уравнение регрессии Y на X действительно имеет линейный вид (1) – (2).

Для проверки гипотезы H₀ вычисляется t-статистика

. (12)

При условии справедливости гипотезы H₀ рассчитанная t-статистика имеет распределение Стьюдента с n – 2 степенями свободы. Найденное по формуле (12) значение сравнивается с критическим значением t_, при  = n – 2 степенях свободы (см. приложение Б). Если расчетное значение по абсолютной величине превосходит табличное для заданного уровня значимости , то нулевая гипотеза H₀ о линейной независимости двух с. в. отклоняется, и с вероятностью ошибки  можно утверждать, что между исследуемыми величинами существует линейная зависимость.

Проверка значимости . При выполнении процедуры проверки значимости оценки коэффициента детерминации выдвигается нулевая гипотеза о том, что предложенное уравнение регрессии никак не отражает реальную зависимость между с. в., т. е. H₀: R² = 0. Альтернативная гипотеза заключается в том, что выбранная модель зависимости (уравнение регрессии) в достаточной степени объясняет действительную зависимость между случайными величинами, т. е. H_a: R² > 0.

Для проверки значимости оценки коэффициента детерминации используется статистика

, (13)

имеющая F-распределение Фишера с ₁ = m – 1 и ₂ = n – m степенями свободы. Здесь m – число неизвестных параметров предполагаемого уравнения регрессии (_ , _ ,…, _m–1 ). Значение статистики, вычисленное по формуле (13) сравнивается с критическим значением F_{1, 2, }, найденным по таблицам квантилей распределения Фишера (приложение Д) при заданном уровне значимости и соответствующем числе степеней свободы. Если F > F_{1, 2, }, то нулевая гипотеза отклоняется, вычисленный коэффициент детерминации значимо отличается от нуля, и с вероятностью ошибки  можно утверждать, что между исследуемыми величинами существует зависимость предложенного вида, и полученное уравнение регрессии может использоваться в дальнейших исследованиях.

Пример 1 По результатам десяти совместных измерений скорости движения локомотива X, км/ч, и соответствующего расхода топлива Y, л/100 км, представленных в таблице 1, следует исследовать зависимость между данными величинами с целью определения «крейсерской» скорости локомотива и прогнозирования величины расхода топлива при заданной скорости движения поезда.

Таблица 1 – Исходные данные

X	40,23	19,63	29,01	89,14	74,96	57,89	34,33	21,01	16,69	9,24
Y	50,66	67,82	60,95	65,53	46,84	52,91	43,71	70,52	67,02	89,96

Решение. На величину расхода топлива локомотивом Y, помимо скорости движения X, влияние оказывает масса состава, профиль и качество железнодорожного полотна, качество подвижного состава, направление и скорость ветра и другие факторы. Поэтому зависимость между величиной расхода топлива локомотивом Y и скоростью движения поезда X является статистической: на одной скорости движения при различных дополнительных условиях расход топлива может принимать различные значения. Для решения поставленной задачи определения «крейсерской» скорости локомотива и прогнозирования величины расхода топлива при заданной скорости движения поезда ограничимся отысканием регрессионной зависимости.

Диаграмма рассеяния, построенная по результатам наблюдений исследуемых величин, представлена на рисунке 4.

Рисунок 4 – Диаграмма рассеяния случайных величин X и Y

Характер расположения точек на диаграмме рассеяния позволяет сделать предположение о параболической регрессионной зависимости

. (14)

Оценки параметров ₀ , ₁ и ₂ найдем методом наименьших квадратов. Для этого составим функцию S(₀ , ₁ , ₂) (см. (3)), которая в случае параболической регрессии примет вид

. (15)

Для отыскания оценок параметров ₀ , ₁ и ₂, минимизирующих функцию S(₀ , ₁ , ₂) , составим и решим систему нормальных уравнений (4):

 

  (16)

Для вычисления значений сумм, входящих в систему уравнений (16), составим расчетную таблицу 2.

Таблица 2 – Результаты промежуточных вычислений

N	xi	yi	xi2	xi yi	xi3	xi4	xi2 yi
1	40,23	50,66	1618,45	2038,05	65110,36	2619389,79	81990,82
2	19,63	67,82	385,34	1331,31	7564,16	148484,53	26133,55
3	29,01	60,95	841,58	1768,16	24414,24	708257,06	51294,31
4	89,14	65,53	7945,94	5841,34	708301,06	63137956,13	520697,42
5	74,96	46,84	5619,00	3511,13	421200,36	31573178,98	263194,03
6	57,89	52,91	3351,25	3062,96	194003,98	11230890,64	177314,75
7	34,33	43,71	1178,55	1500,56	40459,58	1388977,51	51514,37
8	21,01	70,52	441,42	1481,63	9274,24	194851,70	31128,95
9	16,69	67,02	278,56	1118,56	4649,10	77593,50	18668,83
10	9,24	89,96	85,38	831,23	788,89	7289,33	7680,57
	392,13	615,92	21745,5	22484,9	1475766	111086869,2	1229617,6

После подстановки значений система уравнений (16) примет вид:

(17)

Решив систему уравнений (17) известными методами или с помощью MAthCAD, получим следующее решение: ; ; , а уравнение регрессии примет вид

. (18)

На рисунке 5 представлена диаграмма рассеяния случайных величин X и Y с нанесённой линией регрессии.

Рисунок 5 – Диаграмма рассеяния случайных величин X и Y с нанесённой линией регрессии

Оценим качество описания зависимости между величиной расхода топлива локомотивом (Y) и скоростью его движения (Х) полученным уравнением регрессии с помощью коэффициента детерминации (10), где  – значение расхода топлива, предсказываемое уравнением регрессии, при скорости локомотива x_i (см. последний столбец таблицы 3); л/100км – среднеарифметическое наблюденных значений расхода топлива.

Таблица 3 – Значения расхода топлива локомотивом

N	Скорость xi	Наблюденное (фактическое) значение расхода топлива, yi	Значение, предсказываемое уравнением регрессии (xi) = 0 + 1 xi+ 2 xi2
1	40,23	50,66	49,036
2	19,63	67,82	69,091
3	29,01	60,95	57,986
4	89,14	65,53	65,152
5	74,96	46,84	51,248
6	57,89	52,91	44,510
7	34,33	43,71	53,154
8	21,01	70,52	67,250
9	16,69	67,02	73,250
10	9,24	89,96	85,241
	392,13	615,92

Расчётное значение коэффициента детерминации указывает на удовлетворительность описания зависимости между величиной скорости (Х) и расхода топлива (Y), выбранным уравнением регрессии. Проверим, однако, значимость оценки коэффициента детерминации с помощью статистики Фишера

.

Вывод. Критическое значение статистики Фишера для степеней свободы ₁ = 3 – 1 = 2 и ₂ = 10 – 3 = 7 и уровня значимости  = 0,05 составляет . Поскольку расчётное значение статистики Фишера больше критического ( ), то вычисленный коэффициент детерминации значимо отличается от нуля, и выбранное уравнение регрессионной зависимости (18) между величинами скорости и расхода топлива локомотивом может быть использовано в практических целях.

Например, при движении локомотива со скоростью 70 км/ч можно ожидать в среднем расход литров топлива на каждые 100 км пути. Следовательно, можно контролировать фактический расход топлива локомотивом.

Для определения «крейсерской» скорости локомотива (которой соответствует минимальный расход топлива) необходимо решить задачу минимизации функции (см. рисунок 5). Для этого приравняем к нулю производную функции и решим полученное уравнение:

;

       .

Таким образом, «крейсерская» скорость локомотива составляет 55,897 км/ч (см. рисунок 5).

Пример 2 По десяти предприятиям лёгкой промышленности были получены следующие данные об объёмах вкладываемых в предприятие инвестиций X, млрд руб., и соответствующих размерах прибыли Y, млрд руб. (таблица 4).

Таблица 4 – Исходные данные

X	1,0	1,5	4,0	2,5	1,0	0,5	3,0	2,0	0,5	5,0
Y	7,34	11,46	15,35	16,02	3,50	4,95	13,43	7,31	–0,87	17,54

Требуется исследовать зависимость между величинами инвестиций и прибылью, получаемой предприятиями лёгкой промышленности, с целью оптимизации вложения средств.

Решение. Естественно, что на величину прибыли предприятия, помимо величины инвестиций, влияние оказывает большое количество дополнительных факторов (эффективность расходования средств, конъюнктура рынка, величина основных фондов предприятия и др.). Поэтому при исследовании зависимости между величиной инвестиций и прибылью ограничимся отысканием регрессионной зависимости между ними.

Диаграмма рассеяния, построенная по результатам наблюдений исследуемых величин, представлена на рисунке 6.

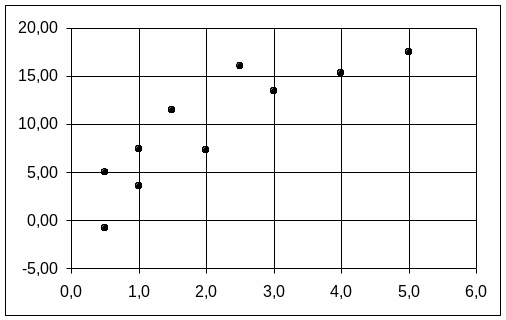
Рисунок 6 – Диаграмма рассеяния случайных величин X и Y

Характер расположения точек на диаграмме рассеяния позволяет сделать предположение о логарифмической регрессионной зависимости вида

. (19)

Оценки параметров ₀ и ₁ найдём методом наименьших квадратов. Для этого составим функцию S (см. (3)), которая в случае логарифмической регрессии примет вид

. (20)

Для отыскания оценок параметров ₀ и ₁, минимизирующих функцию S(₀ , ₁), составим и решим систему нормальных уравнений:

 

  (21)

Результаты вычислений сведём в таблицу 5.

Таблица 5 – Результаты промежуточных вычислений

N	xi	yi	lnxi	ln2xi	yi lnxi	(xi) = 0 + 1 ln xi
1	1,0	7,34	0,0000	0,0000	0,000	6,383
2	1,5	11,46	0,4055	0,1644	4,648	9,148
3	4,0	15,35	1,3863	1,9218	21,286	15,835
4	2,5	16,02	0,9163	0,8396	14,678	12,631
5	1,0	3,50	0,0000	0,0000	0,000	6,383
6	0,5	4,95	–0,6931	0,4805	–3,433	1,657
7	3,0	13,43	1,0986	1,2069	14,749	13,874
8	2,0	7,31	0,6931	0,4805	5,065	11,109
9	0,5	–0,87	–0,6931	0,4805	0,600	1,657
10	5,0	17,54	1,6094	2,5903	28,224	17,357
		96,04	4,7230	8,1644	85,815

После подстановки значений система уравнений (21) примет вид:



Выразив ₀ из первого уравнения и подставив во второе, получим:

откуда ;

.

Таким образом, оценки параметров уравнения регрессии ; [1, MathType™]

На рисунке 7 представлена диаграмма рассеяния значений случайных величин X и Y с нанесённой линией регрессии.

Рисунок 7 – Диаграмма рассеяния случайных величин X и Y с нанесённой линией регрессии

Оценим качество описания зависимости между величиной инвестиций Х и прибыли Y полученным уравнением регрессии с помощью коэффициента детерминации (10),

,

где  – значение величины прибыли, предсказываемое уравнением регрессии, соответствующее значению x_i инвестиции (см. таблицу 5);

 – среднее значение величины прибыли;

Расчётное значение коэффициента детерминации указывает на удовлетворительность описания зависимости между величиной инвестиций Х и прибыли Y, выбранным уравнением регрессии. Проверим, однако, значимость оценки коэффициента детерминации с помощью статистики Фишера

.

Критическое значение статистики Фишера для степеней свободы ₁ = 2 – 1= 1 и ₂ = 10 – 2 = 8 и уровня значимости  = 0,05 составляет . Поскольку расчётное значение статистики Фишера больше критического ( ), то вычисленный коэффициент детерминации значимо отличается от нуля, и выбранное уравнение регрессионной зависимости между величинами инвестиций и прибыли может быть использовано в экономических исследованиях (в частности, для предсказания величины прибыли).

Порядок выполнения работы

1 Изучить теоретические сведения.

2 Получить у преподавателя выборки значений двух исследуемых случайных величин.

3 Создать в ППП STATGRAPHICS файл с выборками исследуемых случайных величин (см. приложение А, п. 2).

4 По заданной двумерной выборке построить диаграмму рассеяния с помощью ППП STATGRAPHICS (приложение А, п. 10).

5 По виду корреляционного поля сделать предположение о форме регрессионной зависимости между исследуемыми случайными величинами.

6 Найти параметры предполагаемого уравнения регрессии вручную методом наименьших квадратов.

7 Оценить качество описания зависимости между исследуемыми случайными величинами и выбранным уравнением регрессии с помощью коэффициента корреляции (в случае линейной зависимости), или с помощью коэффициента детерминации (в случае нелинейной зависимости).

8 Выполнить регрессионный и корреляционный анализ в ППП STATGRAPHICS с помощью процедуры «Multiple Regression» (см. приложение А, п. 8). Сделать распечатку результатов анализа и уравнения регрессии (приложение А, п. 5).

9 Сравнить результаты ручного расчета и компьютерного анализа.

10 Проверить значимость полученного значения коэффициента корреляции (или детерминации) для ручного и компьютерного расчета.

11 Сформулировать общие выводы о зависимости между исследуемыми случайными величинами.

Контрольные вопросы

1 Какая зависимость называется функциональной? Какая зависимость называется статистической? Привести примеры.

2 Какие случайные величины называются независимыми? Привести примеры.

3 Для чего необходим анализ зависимостей между случайными величинами?

4 Что изучает регрессионный и корреляционный анализ?

5 Какая зависимость называется регрессионной?

6 Для чего применяется метод наименьших квадратов?

7 Сформулируйте идею аппроксимации опытных точек на диаграмме рассеяния методом наименьших квадратов.

8 Что характеризует коэффициент корреляции? На что указывают его возможные значения?

9 Что характеризует коэффициент детерминации? На что указывают его возможные значения?

10 Укажите назначение проверки значимости оценки коэффициента корреляции (детерминации).