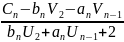- •1.1 Понятие о моделировании.
- •1.2 Системы массового обслуживания
- •2.1. Виды моделирования.
- •2.2Моделирование простейшей одноканальной системы смо
- •3.1. Математическое моделирование. Источники ошибок. Необходимость тестирования.
- •3.2 Простейший поток событий
- •4.1 Необходимость тестирования компьютерных моделей.
- •4.2. Замкнутые смо
- •5.1. Сравнение некоторых пакетов, расчетов и моделирований.
- •5.2. Открытая смо
- •6.1 Примеры задач приводящих к необходимости решения дифференциальных уравнений.
- •6.2 Понятие о конкурирующих стратегиях. Пример алгоритма для выбора рациональной стратегии.
- •7.1 Сведение произвольной системы оду произвольного порядка к системе оду 1-го порядка.
- •7.2 Приближение инженерных данных. Виды приближений.
- •Поточечное среднеквадратическое приближение.
- •Непрерывное приближение в среднеквадратичном смысле.
- •Равномерное приближение.
- •8.1 Примеры сведения дифференциальных уравнений и их систем произвольного порядка к системе оду 1-го порядка в канонической форме Коши.
- •8.2. Интерполирование. Аппроксимация методом наименьших квадратов. Равномерное приближение. Поточечная аппроксимация табличных данных по методу наименьших квадратов.
- •9.1 Пример решения задачи о колебаниях одно массовой системы на основе использования встроенной процедуры Rkadapt.
- •9.2 Разложение аппроксиматора по системе базисных функций. Сведение задачи аппроксимации к системе лау.
- •10.1 Математическое моделирование механических колебательных систем со сосредоточенными параметрами .Системы с распределенными и сосредоточенными параметрами.
- •Пример использования разложения аппроксиматора по базисным функциям в виде мономов.
- •11.1 Методика получения модели механических колебательной системы сосредоточенными параметрами на основе уравнений Лагранжа 2-ого рода
- •11.2Интерполирование, алгебраическое интерполирование, классический подход
- •12.1 Пример получения математической модели для двух массовой колебательной системы
- •12.2 Интерполирование на основе формулы Лагранжа
- •13.1 Математическая модель колебательной системы с вращательными степенями свободы
- •13.2 Пример документа MathCad реализующий поточечную среднеквадратичную аппроксимацию
- •14.1 Некоторые примеры MathCad для решения различных задач
- •14.2 Остаточный член формулы Лагранжа, пример оценки точности интерполирования с использованием остаточного члена
- •15.1 Пошаговые методы решения задачи Коши
- •15.2 О наилучшем выборе узлов интерполирования
- •16.1 Метод Эйлера для решения задачи Коши, реализация этого метод в среде MathCad
- •16.2 Тригонометрическое интерполирование
- •17.1 Модификация метода Эйлера для решения задачи Коши
- •17.2 Использование интерполирования при решении различных задач и реализация в среде MathCad
- •18.1 Метод типа Рунге-Кутта для решения задачи Коши
- •18.2 Использование встроенных функций для линейной аппроксимации по методу наименьших квадратов
- •19.1 Связь модифицированных методов Эйлера и методов Рунге-Кута второго порядка для решения задачи Коши
- •19.2 Понятие о сплайнах
- •20.1 Метод Рунге-Кута 4-ого порядка для решения задачи Коши формулы метода и их реализация в среде MathCad
- •20.2 Определение сплайна. Дефект сплайна, пример линейного сплйна
- •21.1.Оценка погрешности решения оду. Способ Рунге для оценки такой погрешности.
- •21.2 Кубический сплайн дефекта 2 (или сплайн Эрмита).
- •22.1 Метод стрельбы
- •22.2 Кубические сплайны дефекта 1
- •23.1 Использование случайных величин при моделировании различных явлений и процессов
- •23.2 Алгоритм «прогонка» для решения системы линейных уравнений с диагональным преобладанием.
- •24.1 Задача Бюффона как пример использования случайных величин при решении детерминированной задачи.
- •24.2 Пример использования сплайна для приближенного интегрирования функции
- •25.2 Использование параметрических сплайнов для интерполирования кривых
- •26.1 Пример реализации метода типа Монте-Карло в среде Mathcad для вычисления площади произвольной фигуры
- •26.2 Параметрический Эрмитов кубический сплайн.
- •27.1 Основные виды моделирования их преимущества и недостатки
- •27.2 Рациональные сплайны.
- •28.1 Декомпозиция и диакоптика
- •28.2Параметрический рациональный сплайн.
- •29.1 Понятие о компонентных и топологических уравнениях
- •Механическая поступательная система.
- •29.2 О выборе узлов сетки при интерполировании различными сплайнами
- •30.1 Примеры получения эквивалентах схем для механических поступательных систем
- •30.2 Узловой метод построения математической модели
22.2 Кубические сплайны дефекта 1
Это сплайны, которые произошли от гибкой линейки чертёжника при этом в узлах непрерывна должна быть 1-ая и 2-ая производная.
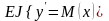 уравнение
изогнутой оси балки, когда заданы
изгибные моменты в каждой точке. По
аналогии 2-ые производные будем называть
моментами.
уравнение
изогнутой оси балки, когда заданы
изгибные моменты в каждой точке. По
аналогии 2-ые производные будем называть
моментами.
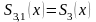
Пусть в n попарно различных точках отрезка [a,b] a<x1<x2<x3….xn=b
y1=f(x1)…. Yn=f(xn)
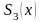 непрерывен
на [a,b]
вместе с 1-ой и 2-ой производной, совпадает
с кубическим полиномом на каждом из
отрезков и удовлетворяет условиям
непрерывен
на [a,b]
вместе с 1-ой и 2-ой производной, совпадает
с кубическим полиномом на каждом из
отрезков и удовлетворяет условиям
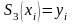 i=1..n
i=1..n
Поскольку
2ая производная по условию в каждом
узле непрерывна, то введя обозначения
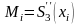 i=1,2…n
и
предположив, что
i=1,2…n
и
предположив, что
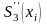 меняется
линейно на интервале
меняется
линейно на интервале
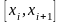 можно записать
можно записать
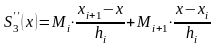 (1)
(1)
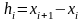
Проинтегрируем
дважды (1). Интегрирование будем выполнять
со скобкой. Тогда после 1-го интегрирования
получим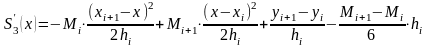 (2)
(2)
А после второго интегрирования получим
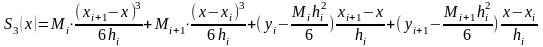 (3)
(3)
Это выражение мы получили для отрезка , аналогичное выражение мы можем получить для предыдущего отрезка
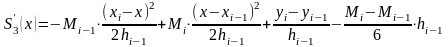 (4)
(4)
Используя условие непрерывности 1-ой производной для узла xi
Для этого приравняем (2) при x=xi к выражению (4) при x=xi . В результате получим
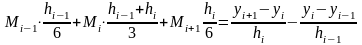 (5)
(5)
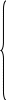
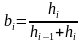
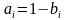
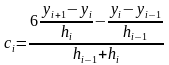 (6)
(6)
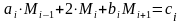 (7)
i=2,3…n-1
(7)
i=2,3…n-1
Т.е. мы получили n-2 линейных алгебраических уравнения относительно Mi
Для замыкания этой системы нужно задать 2 дополнительных уравнения. Эти уравнения можно получить используя условие на концах интервала [a,b] (краевые условия)
1.Периодический сплайн T=b-a.
При этом предполагается, что интерполируемая функция периодическая с T=b-a и поэтому сам сплайн тоже должен быть периодическим с таким же периодом. Запишем условия периодичности:
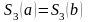
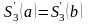
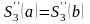
Тогда можно потребовать, чтобы уравнение (7) было справедливо и для i=n, а условие периодичности примет вид
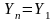
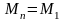
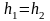
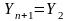
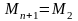
Тогда уравнение (7) примет вид
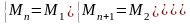 (8)
(8)
2.Непериодический сплайн с заданными наклонами в т a и b
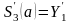 заданное
число
заданное
число
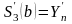 заданное
число
заданное
число
Запишем
уравнение (2) при i=1 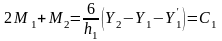
Если
записать уравнение (3) при i=n 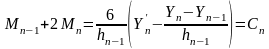
Тогда замыкающая система примет вид
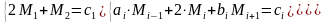 (9)
(9)
Решив системы 8 и 9 можно найти неизвестные M1…..Mn и можем построить сплайн в соответствии с формулой (3)
В некоторых случаях более удобно записывать сплайн в виде набора коэффициентов кубических полиномов вида
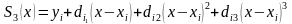 ,
где
,
где
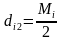
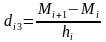
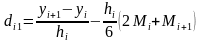 i=1,2..n-1
i=1,2..n-1
23.1 Использование случайных величин при моделировании различных явлений и процессов
Если в к-1 явлении (процессе) присутствуют случайные величины, то оно называется стохастическим, в противном случае процесс называется детерминированным. Случайные величины могут использоваться как при моделировании стохастических явлений так при моделировании детерминированных. Основная идея обычно заключается в том, чтобы сконструировать такой умозрительный процесс поведение которого описывается теми же законами, которыми описывается поведение исходного процесса. Примером является решение задачи Бюффона (24.1)
23.2 Алгоритм «прогонка» для решения системы линейных уравнений с диагональным преобладанием.
Рассмотрим для определенности систему линейных уравнений для непериодического сплайна:
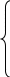 2M1+M2=C1
2M1+M2=C1
aM1+2M2 +b2M3=C2
...
an-1 ∙Mn-2+2Mn-1+bn-1 ∙Mn=Cn-1
Mn-1+2Mn=Cn
Разрешим 1-ое уравнение относительно M1:
M1=p1∙M2+q1
p1=
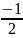 q1=
q1=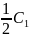
Подставим M1 во 2-ое уравнение и выразим M2:
M2=
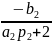 ∙
M3+
∙
M3+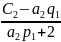
p2=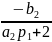 q2=
q2=
M2= p2∙ M3+q2
Продолжая процесс исключения и подставляя Mi-1= pi-1∙ Mi+qi-1 в уравнение
ai ∙Mi-1+2Mi+bi ∙Mi+1=Ci получим:
Mi
=
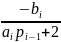 ∙
Mi+1
+
∙
Mi+1
+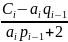 ,
т.е.
pi
и
qi
равны:
,
т.е.
pi
и
qi
равны:
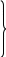 pi=
-рекуррентные
формулы для p
и
q.
(1)
pi=
-рекуррентные
формулы для p
и
q.
(1)
qi=
Продолжая этот процесс, получим для последнего уравнения:
Mn-1= pn-1∙ Mn+qn-1
Mn-1= -2Mn+Cn
Можно последовательно вычислить:
Mn=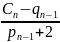 (2)
(2)
Далее можно последовательно вычислить:
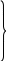 Mn-1=
pn-1∙
Mn+qn-1
Mn-1=
pn-1∙
Mn+qn-1
Mn-2= pn-2∙ Mn-1+qn-2 (3)
и т. д.
Т.о. алгоритм «прогонка» состоит из двух частей: прямой и обратный ход.
В прямом ходе сначала задаем p1 и q1, затем по рекуррентным формулам вычисляем прогоночные коэффициенты.
Обратный ход: сначала по формуле (2) вычисляем Mn , а затем по формулам (3) вычисляют Mn-1, Mn-2, …, M1.
Оказывается, метод «прогонка» не приводит к накоплению ошибок округления при вычислении. Такие методы называются численно устойчивыми.
Сформируем систему для случая периодического сплайна:
Из формул
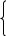 M1=Mn
M1=Mn
ai ∙Mi-1+2Mi+bi ∙Mi+1=Ci , i=2,3,…,h-1.
Mn+1= M2 (hn=h1)
при i=2, M1=Mn получим:
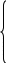 2M2+b2M3+
a2
Mn=C2
2M2+b2M3+
a2
Mn=C2
a3 M2+2M3+ b3 Mn=C3
… (4)
an-1 Mn-2+2Mn-1+ bn-1 Mn=Cn-1
bn ∙Mn-2+an Mn-1+ 2 Mn=Cn
Эти уравнения аналогичны рассмотренному выше приему и их можно переписать:
Mi= pi∙Mi+1 +ri∙Mn+qi , i=2,3,…,n-1 (5)
Прогоночные коэффициенты опять вычисляются по (1) при условии, что pi= qi=0:
ri
=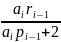 ,r1=1
(6)
,r1=1
(6)
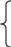 Полагая
Mi=Ui∙Mn+Vi
, i=2,3,…,n-1.
Полагая
Mi=Ui∙Mn+Vi
, i=2,3,…,n-1.
Ui=pi∙Ui+1+ri
Vi=pi∙Vi+1+qi
Un=1 Vn=0
Mn=