20.2 Определение сплайна. Дефект сплайна, пример линейного сплйна

Функция S_n,ν (x) – сплайн степени n дефекта ν, где n и ν - целые числа, если

3. на каждом из отрезков (x_i, x_i+1) из (a,b) функция S_n,ν (x) является полиномом степени n;

4. если S_n,ν (x) на всем интервале (a,b) имеет непрерывные производные до порядка

n- ν включительно.

Кусочные полиномы, образующие сплайн, называются звеньями, а условия непрерывности в узлах­­­____

Рассмотрим сплайн 1-ой степени S₁(x). Он представляет собой непрерывную кусочно-линейную функцию. На каждом из отрезков (x_i, x_i+1) он является полиномом 1-ой степени:

S₁ (x) = A₀+A₁∙x

ν=1, т.е. непрерывной производной он не имеет.

Уравнение сплайна:

S₁(x) = + ( ), x_{i i+1}

h_i =x_i+1 – x_i - шаг

Для построения этого сплайна требуется только таблица (x_i ,y_i). Вычисление этого сплайна можно выполнять по следующему алгоритму:

2. определение tg угла наклона:

tgα_i = =

и вычисляется S₁ (x)= +U_i ∙ (x – x_i ).

(x_i+1,y_i+1)

U_i(x-x_i)

(x_i,y_i) α

S₁(x)

y_i

x_i x x_i+1

Сплайн 1-ой степени относится к семейству локальных сплайнов, т.к. для его построения необходима информация только об ограничивающих данный участок узлах.

21.1.Оценка погрешности решения оду. Способ Рунге для оценки такой погрешности.

Основная цель приближённых вычислений заключается в нахождении результата с заданной степенью точности. В частности для оценки точности решения ДУ можно использовать такие способы:

1. Проверка выполнения условия задачи (например данное численное решение можно подставить в само ДУ и сравнить расхождение с его правой частью)

2. Двойной пересчет по возможности другим методом

3. Применение упрощённой расчетной схемы и качественный анализ задачи.

Локальная погрешность тем меньше, чем меньше шаг, в то же время при большом количестве шагов суммарная погрешность может возрастать. Если же шаг увеличить хотя время решения задачи сократится полученная точность может не удовлетворять исследователя. Для приближенной оценки точности решения можно использовать способ Рунге.

Способ Рунге для оценки такой погрешности.

Предполагает, что на зад. интервале решение выполняется с постоянным по величине шагом, а затем решение выполняется с удвоенным по величине шагом H=2h. Пусть при этом используется метод m-го порядка точности. Тогда на отдельном шаге h величина локальной погрешности составит: .

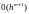Предполагаем, что c шагом h выполняется 2n шагов, тогда Н→n.

Предположение на котором основан метод Рунге заключается в том, что на отдельном шаге погрешность равна:

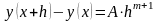
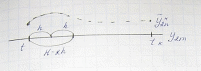
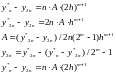
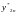- приближенное решение в конечной точке t_k после 2n шагов величины h.

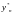- приближенное решение в точке t_k после n шагов величиной H=2h.

Y_2n – неизвестное решение.

Считая на каждом шаге погрешность одинаковой, можно записать:

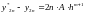
При вычислении с удвоенным шагом:

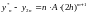
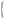
Система двух уравнений с двумя неизвестными A и Y_2n. Решая, получим:

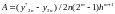
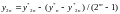
_{Уклонение точного решения от приближенного:}

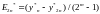
_{В частности для более распространенного метода Рунге-Кутта 4-го порядка (m=4):}

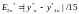
_{Ещё раз заметим, что в основе этой оценки лежит предположение, что на отдельном шаге погрешность равна}