15.1 Пошаговые методы решения задачи Коши

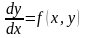(1) – ОДУ первого порядка

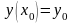(2) – начальные условия

(1)+(2) – задача Коши

Поясним необходимость условия (2)

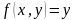
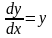(3)

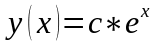с – произвольная константа

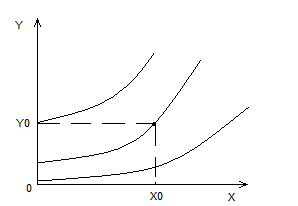Рис.1 семейство решений уравнения (3)

Для того, чтобы выбрать одно конкретное необходимо указать через какую точку в плоскости оно проходит. При этом получить аналитическое решение удаётся крайне редко.

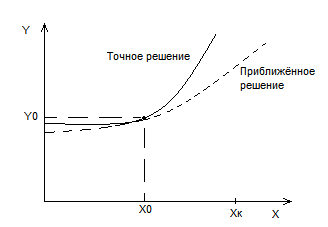Рис.2 точное и приближенное решение

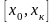- интервал наблюдения. Это приближенное решение строят по шагам

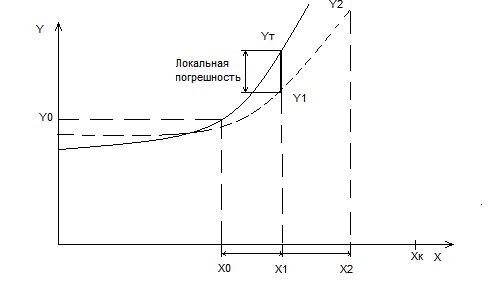Рис.3

Если взять отдельный шаг, то уклонение приближенного решения от точного называется локальной погрешностью метода. Локальная погрешность зависит от величины шага h - 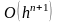, где n - порядок метода.

Величина шага может быть как постоянной так и переменной. Метод может быть одношаговым (само стартующим) и многошаговым (не само стартующим).

Формула для вычисления решения на следующем шаге:

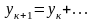зависит от у_к

или

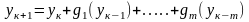
Проиллюстрировать можно следующим образом:

А)одношаговый

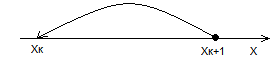
Б)многошаговый

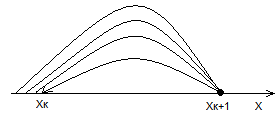
Метод называется само стартующим поскольку для его запуск нужно знать только начальное условие. В противном случае метод называется не само стртующим.

15.2 О наилучшем выборе узлов интерполирования

зависит от расположения узлов на интервале интерполирования. Для сравнения приведем значения и соответствующей таблицы: ln(2,5)=0,9163.Пусть f(x) – интерполируемая функция. Заменим эту функцию полиномом Лагранжа: f(x)=L_n-1+R(f,x). R(f,x) – остаточный член формулы Лагранжа, который представляет собой погрешность метода интерполяции. При выполнения вычисления, результаты отдельных арифметических операций округляются или отсекаются из разряда, поэтому при построении интерполяционного полинома кроме погрешности метода будет присутствовать еще вычислительная погрешность. Можно доказать следующие утверждение: если функция f(x) n раз непрерывно дифференцируема на отрезке [a,b], содержащем узлы интерполирования x₁, x₂, …., x_n, то такая что , где w_n(x)= . Пусть M_n= , . Понятно, чтобы использовать эту теорему нужно иметь возможность взять производную . Интерполяционный полином можно построить единственным образом по данным таблицы. Остаточный член R(f,x) всегда имеет один и тот же вид. Возникает вопрос: Можно ли выбрать такое количество узлов на интервале интерполирования, чтобы w_i(x) имело наименьшее максимальное значение на интервале (a,b) из всех возможных? Чебышев доказал, что наилучшим выбором узлов будет следующий:

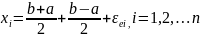
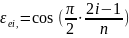
В этом случаи: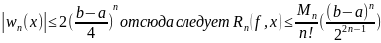

Узлы х_i не являются равностоящими, а сужаются у концов интервала интерполирования.

16.1 Метод Эйлера для решения задачи Коши, реализация этого метод в среде MathCad

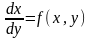Проинтегрируем обе части этого уравнения на очередном интервале Х_к X_к+1 В точке X_k решение уже получено

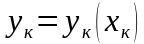
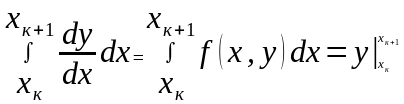
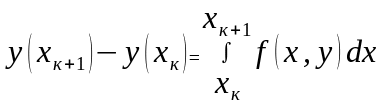
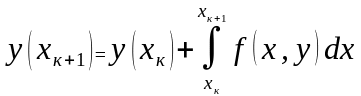
Разные методы интегрирования отличаются формулами, которые используются для приближенного вычисления интеграла входящего в правую часть

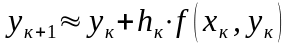
Это метод первого порядка точности

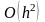
16.2 Тригонометрическое интерполирование

Алгебраическая интерполяция в качестве базисных функций использует мономы. Если же интерполируемая функция является периодической, то уместно в качестве базисных функций выбирать периодические функции. Будем рассматривать ситуацию, когда f(x), которую следует приблизить является периодической на интервале [a,b]. Пусть узлы являются равностоящими, т.е.:

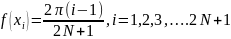
В качестве базисных функций используем: cos 0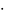 x, sin 0 x, cos 1 x, sin 1 x,………cos k x, sin k x.

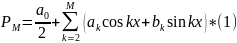
Задача тригонометрической интерполяции состоит в построении тригонометрического интерполируемого полинома вида *(1) , удовлетворяющего условию: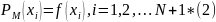 . Можно показать, что коэффициенты интерполяционного полинома

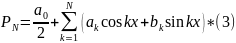
Удовлетворяют условию *(2) вычисленных по формулам:

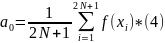
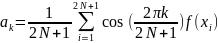
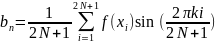
Достаточно строгого класса функции, чтобы утверждать, что при увеличении N ошибка интерполирования стремится к нулю. Формулы *(4) можно распространять и на функции интерполирования на случаи периодической функции на отрезке [a,b] с периодом