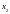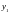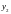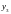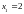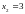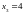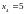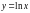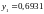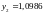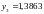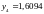- •1.1 Понятие о моделировании.
- •1.2 Системы массового обслуживания
- •2.1. Виды моделирования.
- •2.2Моделирование простейшей одноканальной системы смо
- •3.1. Математическое моделирование. Источники ошибок. Необходимость тестирования.
- •3.2 Простейший поток событий
- •4.1 Необходимость тестирования компьютерных моделей.
- •4.2. Замкнутые смо
- •5.1. Сравнение некоторых пакетов, расчетов и моделирований.
- •5.2. Открытая смо
- •6.1 Примеры задач приводящих к необходимости решения дифференциальных уравнений.
- •6.2 Понятие о конкурирующих стратегиях. Пример алгоритма для выбора рациональной стратегии.
- •7.1 Сведение произвольной системы оду произвольного порядка к системе оду 1-го порядка.
- •7.2 Приближение инженерных данных. Виды приближений.
- •Поточечное среднеквадратическое приближение.
- •Непрерывное приближение в среднеквадратичном смысле.
- •Равномерное приближение.
- •8.1 Примеры сведения дифференциальных уравнений и их систем произвольного порядка к системе оду 1-го порядка в канонической форме Коши.
- •8.2. Интерполирование. Аппроксимация методом наименьших квадратов. Равномерное приближение. Поточечная аппроксимация табличных данных по методу наименьших квадратов.
- •9.1 Пример решения задачи о колебаниях одно массовой системы на основе использования встроенной процедуры Rkadapt.
- •9.2 Разложение аппроксиматора по системе базисных функций. Сведение задачи аппроксимации к системе лау.
- •10.1 Математическое моделирование механических колебательных систем со сосредоточенными параметрами .Системы с распределенными и сосредоточенными параметрами.
- •Пример использования разложения аппроксиматора по базисным функциям в виде мономов.
- •11.1 Методика получения модели механических колебательной системы сосредоточенными параметрами на основе уравнений Лагранжа 2-ого рода
- •11.2Интерполирование, алгебраическое интерполирование, классический подход
- •12.1 Пример получения математической модели для двух массовой колебательной системы
- •12.2 Интерполирование на основе формулы Лагранжа
- •13.1 Математическая модель колебательной системы с вращательными степенями свободы
- •13.2 Пример документа MathCad реализующий поточечную среднеквадратичную аппроксимацию
- •14.1 Некоторые примеры MathCad для решения различных задач
- •14.2 Остаточный член формулы Лагранжа, пример оценки точности интерполирования с использованием остаточного члена
- •15.1 Пошаговые методы решения задачи Коши
- •15.2 О наилучшем выборе узлов интерполирования
- •16.1 Метод Эйлера для решения задачи Коши, реализация этого метод в среде MathCad
- •16.2 Тригонометрическое интерполирование
- •17.1 Модификация метода Эйлера для решения задачи Коши
- •17.2 Использование интерполирования при решении различных задач и реализация в среде MathCad
- •18.1 Метод типа Рунге-Кутта для решения задачи Коши
- •18.2 Использование встроенных функций для линейной аппроксимации по методу наименьших квадратов
- •19.1 Связь модифицированных методов Эйлера и методов Рунге-Кута второго порядка для решения задачи Коши
- •19.2 Понятие о сплайнах
- •20.1 Метод Рунге-Кута 4-ого порядка для решения задачи Коши формулы метода и их реализация в среде MathCad
- •20.2 Определение сплайна. Дефект сплайна, пример линейного сплйна
- •21.1.Оценка погрешности решения оду. Способ Рунге для оценки такой погрешности.
- •21.2 Кубический сплайн дефекта 2 (или сплайн Эрмита).
- •22.1 Метод стрельбы
- •22.2 Кубические сплайны дефекта 1
- •23.1 Использование случайных величин при моделировании различных явлений и процессов
- •23.2 Алгоритм «прогонка» для решения системы линейных уравнений с диагональным преобладанием.
- •24.1 Задача Бюффона как пример использования случайных величин при решении детерминированной задачи.
- •24.2 Пример использования сплайна для приближенного интегрирования функции
- •25.2 Использование параметрических сплайнов для интерполирования кривых
- •26.1 Пример реализации метода типа Монте-Карло в среде Mathcad для вычисления площади произвольной фигуры
- •26.2 Параметрический Эрмитов кубический сплайн.
- •27.1 Основные виды моделирования их преимущества и недостатки
- •27.2 Рациональные сплайны.
- •28.1 Декомпозиция и диакоптика
- •28.2Параметрический рациональный сплайн.
- •29.1 Понятие о компонентных и топологических уравнениях
- •Механическая поступательная система.
- •29.2 О выборе узлов сетки при интерполировании различными сплайнами
- •30.1 Примеры получения эквивалентах схем для механических поступательных систем
- •30.2 Узловой метод построения математической модели
12.1 Пример получения математической модели для двух массовой колебательной системы
q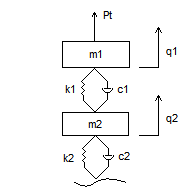 1
–
линейное перемещение верхней массы
1
–
линейное перемещение верхней массы
q2 – нижней
q1, q2 – абсолютное перемещение (от земли)
 -
уровень
земли
-
уровень
земли
Выразим
удлинение упругих элементов конструкции
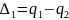 и
и
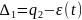 Найдём:
Найдём:

12.2 Интерполирование на основе формулы Лагранжа
Один из наиболее распространенных способов построения интерполяционного полинома.
Введем
предварительно в рассмотрение так
называемые полиномы
влияния
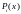 .
.
Этот полином должен удовлетворять следующим условиям:
степень полинома должна быть равна (n-1);
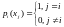
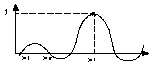
Очевидно, что полином степени (n-1) , равный нулю во всех узлах кроме i- того, имеет вид:
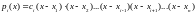
Остается
определить константы С из условия
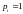
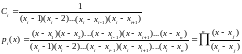
Полином
Лагранжа обычно обозначают
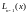 .
.
Очевидно, что
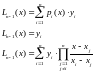
Рассмотрим два частных случая полинома Лагранжа:
Пусть имеется таблица из двух точек
|
|
|
|
Тогда интерполирующий полином будет выглядеть
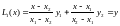
Это так называемый случай линейной интерполяции, поскольку данное уравнение - это уравнение прямой.
Пусть имеется таблица из n=3 точек
|
|
|
|
|
|
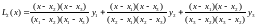
Такое приближение называется параболическим или квадратическим (так как данное уравнение- уравнение параболы).
Рассмотрим пример.
Пусть задана таблица
|
|
|
|
|
|
|
|
|
|
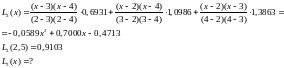
13.1 Математическая модель колебательной системы с вращательными степенями свободы
q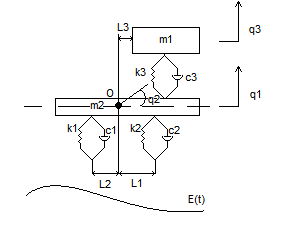 1-
смещение корпуса автомобиля массой m2
в вертикальном направлении относительно
дороги
1-
смещение корпуса автомобиля массой m2
в вертикальном направлении относительно
дороги
q2 – угол поворота рамы автомобиля отсчитываемый от дороги относительно центра тяжести
q3- перемещение массы m1 отсчитываемое от рамы автомобиля
Выразим абсолютное перемещение абсолютные скорости и удлинения пружин и скорости удлинения демпферов. Будем при этом считать колебания малыми т.е. угол поворот q 2 <<1.


13.2 Пример документа MathCad реализующий поточечную среднеквадратичную аппроксимацию
поточечная
среднквадаичная аппроксимция
x
и y координаты узлов
длина
массива x
Cистема
базисных фукций
![]()
![]()

![]()
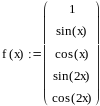
![]()
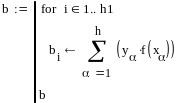
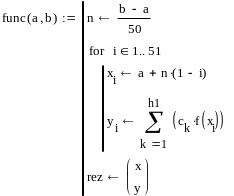
![]()
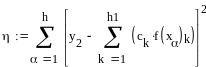
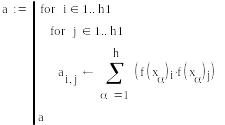

Вычисление
коэф на основе функции Minimize пример
для
функции 2ух пременных
x
и y координаты узлов
базисные
![]()
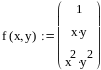
![]()
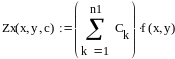
![]()
![]()
начальное
зачение для неизв коэф
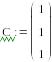
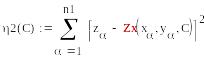
![]()
![]()
14.1 Некоторые примеры MathCad для решения различных задач

14.2 Остаточный член формулы Лагранжа, пример оценки точности интерполирования с использованием остаточного члена
Интерполяционная формула Лагранжа это один из наиболее распространенных способов построения интерполяционного полинома. Пусть имеем функцию:

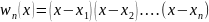 зависит
от расположения узлов на интервале
интерполирования. Для сравнения приведем
значения и соответствующей таблицы:
ln(2,5)=0,9163.
зависит
от расположения узлов на интервале
интерполирования. Для сравнения приведем
значения и соответствующей таблицы:
ln(2,5)=0,9163.
Пусть
f(x)
– интерполируемая функция. Заменим эту
функцию полиномом Лагранжа:
f(x)=Ln-1+R(f,x).
R(f,x)
– остаточный член формулы Лагранжа,
который представляет собой погрешность
метода интерполяции. При выполнения
вычисления, результаты отдельных
арифметических операций округляются
или отсекаются из разряда, поэтому при
построении интерполяционного полинома
кроме погрешности метода будет
присутствовать еще вычислительная
погрешность. Можно доказать следующие
утверждение: если функция f(x)
n
раз непрерывно дифференцируема на
отрезке [a,b],
содержащем узлы интерполирования x1,
x2,
…., xn,
то
 такая что
такая что
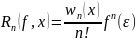 ,
где wn(x)=
,
где wn(x)=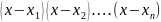 .
Пусть Mn=
.
Пусть Mn=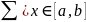 ,
,
 .
Понятно, чтобы использовать эту теорему
нужно иметь возможность взять производную
.
Понятно, чтобы использовать эту теорему
нужно иметь возможность взять производную
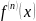 .
Интерполяционный полином можно построить
единственным образом по данным таблицы.
Остаточный член R(f,x)
всегда имеет один и тот же вид.
.
Интерполяционный полином можно построить
единственным образом по данным таблицы.
Остаточный член R(f,x)
всегда имеет один и тот же вид.