17.1 Модификация метода Эйлера для решения задачи Коши

Если заменить площадь криволинейной трапеции, представляющей собой величину этого интергала, например, на площадь прямоугольника

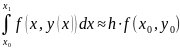
y₀

X

y=y(x)

Y

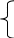
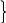
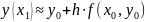- Ф-ла Эйлера реализующая метод Эйлера. Можно показать, что локальная погрешность этой ф-лы 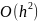, т.е. метод Эйлера является методом 1-го порядка точности.

X₀

X₁

α₀

h

Δy

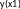
Модификации метода Эйлера

h

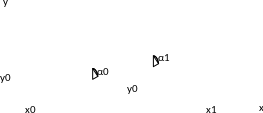
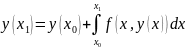
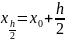
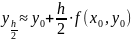
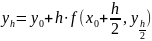Можно показать, что погрешность этой ф-лы – 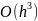– метод 2-го порядка. Точность увеличивается на порядок, но приходится ещё раз обращаться к правой части ДУ

Усовершенствованный метод Эйлера

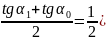
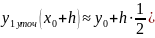
Метод с погрешностью

17.2 Использование интерполирования при решении различных задач и реализация в среде MathCad

У нас задачи интерполирования заключались в том, чтобы в узлах совпадало только значение функции. Понятно, что аналогичную задачу можно сформулировать выдвигая требования, чтобы в узлах совпадали ешё и значения производных. Если говорить только о первых производных, то задача решается с помощью полином Эрмита, которые будут аналогами базисных функций. Кроме того в некоторых ситуациях нужно выполнять интерполяцию для функции нескольких переменных.

Идея интерполирования лежит в основе многих методов приближенных вычислений:

1) приближенные вычисления функции

2) численное интегрирование

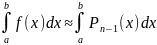
Т.е. подинтегрированную функцию f(x) заменяют интерполяционным полиномом, а затем от него вычисляется определенный интеграл. Операция приближенного интегрирования основана на этом подходе достаточна точна.

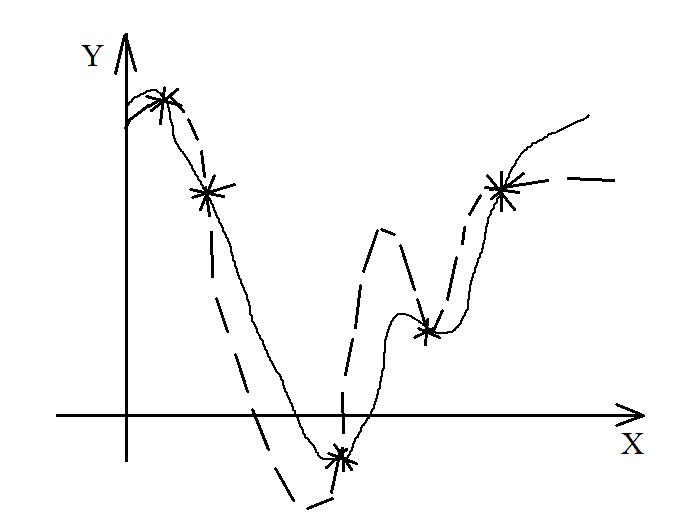Тоже справедливо и для функций заданных таблично:

3) Численное дифференцирование

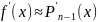
К сожалению эта операция имеет приближенную точность:

4) Численное решение

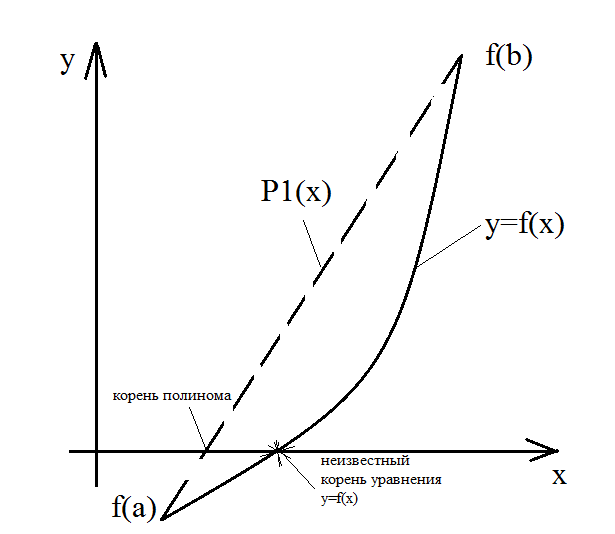
алгебраических и тангенциальных уравнений:

Пусть исходная функция f(x) задана аналитически на интервале [a,b] и её значения могут быть вычислены в нужных точках. Пусть f(x)=0 – корень этого уравнения уединен на интервале [a,b], тогда по значениям этой функции в узлах строят интерполяционный полином, находят его корень на этом интервале и считают, что он приблизительно равен корню уравнения на этом интервале.

18.1 Метод типа Рунге-Кутта для решения задачи Коши

y(x+h) = y(x) +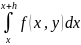

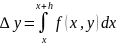
Выполним замену переменной

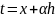
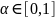
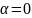t=x

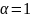t=x+h

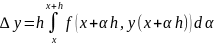
Введем три набора параметров

…..

…..

………………

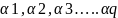
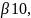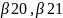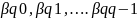
A0,A1,…..Aq

При помощ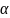и и 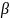наборов будем последовательно вычислять величины.

………..

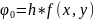
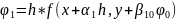
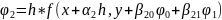
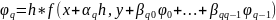
Эти величины могут быть вычислены последовательно. Теперь при помощи параметров группы А составим линейную компбинацию.

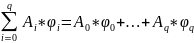
Будем приближать величину 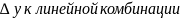т.е.

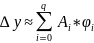Погрешность этого приближения обозначим 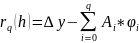. Разложим по формуле Тейлора

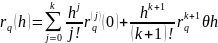
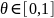(1) Основная идея этого подхода в том, чтобы подобрать такие наборы (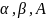 ), которые обеспечили бы как можно лучшее приближение 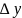к составленной линейной комбинации. Это значит, что при произвольной функции f в выражении 1 как можно большее количество слагаемых в формуле Тейлора оказались =0 т.е. чтобы 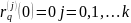для как можно большего k.

Методы 1-го порядка точности.

Пусть q=0 тогда А₀ тогда 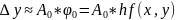после вычисления

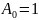
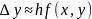
y(x+h)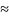 y(x)+hf(x,y) Мы получим формулу метода Эйлера, это значит что частный случай метода Рунге-Кутта.