8.3 Нормальний закон розподілу випадкових величин

У теорії імовірності доведено, що сума різних незалежних випадкових доданків (незалежно від їхнього закону розподілу) виявляється випадковою величиною, розподіленою відповідно до нормального закону (т.зв. центральна гранична теорема). Тому нормальний розподіл гарно моделює саме широке коло явищ, для яких відомо, що на них впливають кілька незалежних випадкових факторів. Для великої кількості випадків, що зустрічаються на практиці, випадкові величини розподіляються саме за нормальним законом розподілу (законом Гауса). Якщо випадкові величини, розташувати по осі абсцис в порядку зростання, а по осі ординат їх густину імовірності, то побудувавши графік отримаємо криву, зображену на малюнку 8.4 (в прикладі для побудови графіка застосовано генератор випадкових величин і спеціальна функція dnorm(), які будуть розглянуто пізніше).

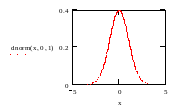
Мал.8.4 Крива нормального розподілу випадкової величини

Теорія показує, що істинному значенню випадкової величини х відповідає те значення, для якого густина імовірності найбільша. Випадкові величини розподіляються симетрично по обидві сторони від цієї точки. В теорії імовірності значення цієї точки отримало назву - математичне очікування, а сама точка – центр розподілу. Крива нормального розподілу охоплює всі можливі значення вимірюваної величини, тому вся площа , обмежена кривою, дорівнює 1.

8.4 Характеристики нормального розподілу

• Математичне очікування. Середнє значення.

Математичним очікуванням М(х) дискретної випадкової величини х називається сума добутків всіх можливих значень випадкової величини помножена на імовірність цих значень р_і і записується формулою:

М(х)= х_і р_і. (8.3)

Для неперервних випадкових величин просте сумування неможливе. Тому математичне очікування записується наступним чином:

М(х)=_- х  (х) dx, (8.4)

де x – випадкова величина;

(х) – ординати для кожного значення х;

dx – елементарні відрізки осі абсцис.

Якщо розглядати нормальний розподіл випадкових величин (Малюнок 8.4), то математичне очікування буде відповідати істинному значенню випадкової величини х. На практиці для визначення істинного значення випадкової величини приймають середнє арифметичне значення ряду випадкових величин, що обчислюється за формулою:

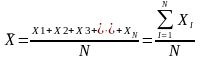, (8.5)

де 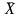- середнє значення;

х_і –поточне значення випадкової величини;

N – число випадкових величин.

Доказано, що середнє арифметичне значення являється наближеним до істинного значення, тобто його математичним очікуванням для даних умов вимірювання. На малюнку 8.4 середнє значення, а значить і істинне значення випадкової величини дорівнює нулю.

• Дисперсія

Криві нормального розподілу можуть мати різний вигляд. На малюнку 8.5

наведено приклади кривих нормального розподілу випадкових величин з різним математичним очікуванням і розкидом результатів вимірювання.

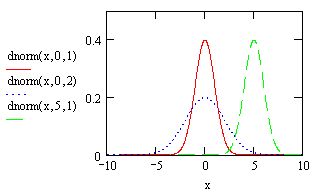
Мал. 8.5. Криві нормального розподілу

Крива 1, позначена суцільною лінією, – вся площина зосереджена біля ординати, а значить більшість результатів мало відрізняється від математичного очікування, що дорівнює нулю;

Крива 2, позначена крапками, – площина розосереджена, має великий розкид результатів. Тут математичне очікування теж дорівнює нулю.

Крива 3, позначена штриховою лінією, – вся площина зосереджена біля математичного очікування, що дорівнює п’яти. Розкид випадкових величин такий же, як у кривій 1.

Мірою розсіювання (розкиду) випадкових величин служить дисперсія D(x), що позначається ².

Дисперсія дискретних випадкових величин визначається як:

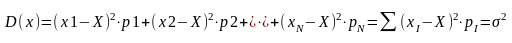(8.6)

Дисперсія неперервних випадкових величин записується формулою

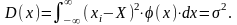(8.7)

• Середнє квадратичне відхилення

Для характеристики розсіювання частіше всього користуються середнім квадратичним відхиленням, що визначається як корінь квадратний від дисперсії.

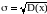(8.8)

Теоретично доказано, що для отримання  за результатами експериментальних даних середнє квадратичне відхилення потрібно визначати в іншому нормуванні за формулою:

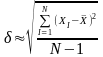
Чим більше вимірювань N, тим точніше визначено  .

• Коваріація і кореляція

Функції, що встановлюють зв'язок між парами двох випадкових векторів, називаються коваріацією і кореляцією.(або по іншому коефіцієнтом кореляції). Вони розрізняються нормуванням, як це витікає з визначення. Для двох випадкових величин x та y коваріація визначається за формулою

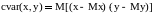, (8.10)

де Mx та My – математичні очікування випадкових величин x і y. Для незалежних випадкових величин коваріація дорівнює нулю.

Коефіцієнт кореляції є коваріація нормована на корінь квадратний з добутків дисперсій Dx та Dy випадкових величин:

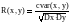(8.11)

Кореляція визначається за формулою:

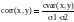, (8.12)

• де 1, 2 - середні квадратичні відхилення випадкових величин.