19. Розв’язок систем лінійних алгебраїчних рівнянь

Розв’язок систем лінійних алгебраїчних рівнянь

Центральним питанням обчислювальної лінійної алгебри є розв’язок систем лінійних алгебраїчних рівнянь (СЛАУ), тобто систем рівнянь виду ( як приклад розглядаємо систему з трьох рівнянь з трьома невідомими):

(1)

У матричній формі СЛАУ записується в еквівалентному вигляді:

(2)

СЛАУ має єдиний розв’язок, якщо матриця А є не виродженою, тобто її визначник не дорівнює нулю. У Mathcad СЛАУ можна розв’язати як у більш наочній матричній формі (1), так і в більш зручній для запису та наочній формі (2). Для першого способу варто використовувати вбудовану функцію Isolve , а для другого - обчислювальний блок Given / Find. Функція Isolve має таку структуру:

- lsolve (А,B) – розв’язок системи лінійних рівнянь;

А - матриця коефіцієнтів системи;

B - вектор правих частин.

Застосування функції Isolve показано в прикладі 5.6, а обчислювального блоку Given / Find в прикладі 5.7.

Вбудовану функцію Isolve допускається застосовувати і при символьному розв’язку СЛАУ.

Приклад 5.6 Розв’язок СЛАУ матричним способом за допомогою функції Isolve

У випадку розв'язку системи нелінійних рівнянь з допомогою блоку Given / Find , її розв’язується точно так само, як і системи нелінійних рівнянь. Треба не забувати, що в цьому випадку застосовуються чисельні методи розв’язку, які вимагають перед записом блоку привласнювання всім невідомим початкових значень (це зроблено в першому рядку прикладу 5.7). Вони можуть бути довільними, тому що розв’язок СЛАУ з не виродженою матрицею єдиний. Невідомі в цьому випадку позначені змінними x, y та z

Приклад 5.7 Розв’язок СЛАУ за допомогою обчислювального блоку

Розв’язок СЛАУ можна також отримати за допомогою обчислювального блоку з функцією Minerr, а також використовуючи в матричному варіанті розв’язку оберненої матриці (приклад 5.8).

Приклад 5.8 Розв’язок СЛАУ за допомогою оберненої матриці

21. Закони розподілу випадкових величин

Основи законів розподілу випадкових величин

Якщо розташувати дискретні випадкові величини в порядку зростання і позначити їх через x₁, x₂, x₃, x₄,…,x_n, а відповідні їм імовірності через p₁, p₂, p₃, p₄,…p_n, то можемо отримати таблицю 8.1 виду:

Таблиця 8.1 Ряд імовірностей випадкових дискретних величин

x1	x2	x3	…	xn
p1	p2	p3		pn

Якщо прийняти n=9, x₁ =0, а інтервали між сусідніми значення дискретної величини однаковими і рівними одиниці, то розподіл випадкових дискретних величин можна подати у вигляді, наприклад, таблиці 8.1 і побудувати графік розподілу (Мал.8.1):

Таблиця 8.2 Приклад ряду імовірностей випадкових дискретних величин

xn	0	1	2	3	4	5	6	7	8
pn	0	0.025	0.075	0.125	0.175	0.0125	0.075	0.025	0

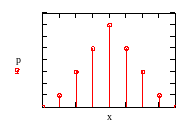
Мал.8.1 Графік розподілу дискретної випадкової величини

Сума всіх ординат повинна дорівнювати одиниці. Ми можемо взяти любий інтервал зміни х і визначити імовірність того, що значення х лежить в його межах, просумувавши ординати графіка в межах інтервалу.

Створити таблицю всіх можливих значень неперервних випадкових величин неможливо, так як їх число в любому інтервалі нескінченно велике. Звідси витікає, що імовірність любого значення неперервної випадкової величини нескінченно мала. Щоб вияснити розподіл імовірностей інтервал зміни аргументу ділять на ряд інтервалів і визначають для кожного з них імовірність того, що значення х не вийде за його межі. За значеннями імовірностей, знайдених для всіх інтервалів, будують ступінчасту криву, що називається гістограмою (Малюнок 8.2). Основа кожного прямокутника цієї кривої відповідає вибраному інтервалу величини, а висота – імовірності. Оскільки значення імовірності відноситься не до одного значення величини, а до її інтервалу, то говорять про густину імовірності для деякого інтервалу. Площа кожного прямокутника пропорційна густині імовірності для заданого інтервалу.

Мал.8.2 Графік розподілу неперервної випадкової величини

Якщо взяти малі інтервали між сусідніми значеннями величин, визначити густину імовірності для кожного з них і побудувати криву. То вона втратить ступінчастий характер і перейде в плавну криву, що називається кривою густини розподілу імовірності (Малюнок 8.3 – для наведеного прикладу).

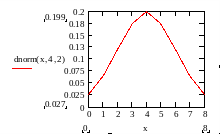
Мал.8.3 Крива густини розподілу імовірностей випадкової величини

Ордината кривої характеризує густину імовірності в даній точці. Площа під усією кривою рівна імовірності появи любої з можливих значень випадкової величини х_і, тобто вона дорівнює одиниці. Щоб визначити, яка імовірність того, що значення х_і буде лежати в деяких межах, наприклад [x_a;x_b], визначають площу, що лежить між ординатами, проведеними в точках x_a та x_b.Ця площа пропорційна густині імовірності для заданого інтервалу.