12 Линии влияния в арках.

Построение линий влияния внутренних усилий в арке основываются на тех выводах, которые мы получили ранее при расчете на статическую нагрузку:

Вертикальные опорные реакции в арке и аналогичной балке одинаковы. Естественно, что и линии влияния также будут одинаковы (рис. 7.3).

Распор H был найден через значение по формуле:

Воспользуемся ей для построения линии влияния распора. Учтем, что f есть стрела подъема арки, т.е. величина постоянная. Тогда л.в. H представляет собой л.в. , ординаты которой уменьшены в f раз (рис. 7.3).

Для определения изгибающего момента в любом сечении арки была получена формула:

.

Для нашего случая (сечение n) она примет следующий вид:

Применим ее для построения л.в. Mn. Построим линию влияния для балки. Л.в. распора H у нас уже построена (рис. 7.3) однако ее ординаты надо увеличить на yn. Постоим л.в. Hyn с той же стороны оси, что и л.в. Mn, так как имеем разность линий влияния. Заштриховав участки между двумя линиями влияния, получим л.в. Mn.

Удобней пользоваться выпрямленной л.в. Mn (рис.7.3). При выпрямлении не надо забывать о знаках полученной ранее линии влияния.

4. Линия влияния Qn строится по формуле:

.

Надо построить л.в. – л.в. поперечной силы в сечении n для балки, ординаты которой увеличим на . Затем наложим на нее л.в. H, ординаты которой увеличены на . Заштриховав участки между двумя линиями влияния, получим л.в. (рис. 7.3). Выпрямим ее с учетом знаков.

5. Линию влияния Nn построим по формуле:

.

Принцип ее построения тот же, что и ранее, но так как у нас сумма двух линий влияния, то откладывать их надо по разные стороны от оси (рис.7.3).

Расчет по л.в. от постоянной нагрузки усилий ведется по ранее полученным формулам, а искомые ординаты определяются из подобия треугольников.

На приведенных линиях влияния даны значения тех ординат, через которые можно найти любые другие, что вам предстоит проделать самостоятельно.

15 Работа внутр сил теорема клаиперона взамозависимость перемещения от работы.

При загружении сооружения статической внешней нагрузкой работу совершают и внутренние усилия.

Выделим из стержня двумя близкими сечениями, перпендикулярными к его оси, бесконечно малый элемент dx (рис. 8.2). Он будет находиться в состоянии статического равновесия под действием возникающих в сечении усилий M, Q, N. Усилия M, Q, N являются внешними усилиями по отношению к выделенному элементу dx, поэтому работу А, совершаемую ими найдем по теореме Клапейрона. Воспользуемся принципом независимости действия сил и рассмотрим работу каждой силы в отдельности. Левое сечение закрепим в последующих случаях защемлением..

Р абота растягивающей силы N . Рассмотрим элемент dx, к которому приложено вдоль оси растягивающее усилие N (рис. 8.3). Элементарная работа силы N, приложенной статически к бесконечно малому элементу dx будет:

.

Найдем величину абсолютной деформации х. Воспользуемся известными сведениями из сопротивления материалов:

, откуда .

Величину относительной деформации найдем из закона Гука:

.

Величину нормального напряжения можно найти из:

, где А – площадь поперечного сечения.

Воспользовавшись представленными выражениями, найдем, что:

.

Работа сдвигающей силы Q. Рассмотрим элемент dx, к которому приложено сдвигающие (касательное к сечению) усилие Q (рис. 8.4). Элементарная работа силы Q, приложенной статически к бесконечно малому элементу dx будет:

.

Найдем перемещение y.

в силу малости угла сдвига. Тогда

y = dx.

Для определения  воспользуемся законом Гука:

.

К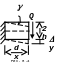 асательное напряжение найдем по формуле Журавского:

, тогда

и .

Мы специально ввели в числитель и знаменатель площадь поперечного сечения и разбили выражение на произведение двух частей, первая из которых связана только с геометрическими характеристиками поперечного сечения и при постоянном сечении по длине стержня будет величиной постоянной. Обозначим:

.

Тогда элементарная работа сдвигающей силы Q будет равна:

.

Работа изгибающего момента М. Рассмотрим элемент dx, к которому приложен сосредоточенный момент М (рис. 8.5). Элементарная работа изгибающего момента по теореме Клапейрона равна:

.

Найдем угол поворота сечения d:

.

Относительная деформация , откуда x = dx.

Воспользовавшись законом Гука при чистом изгибе (отсутствуют поперечные силы в сечении) и учитывая, что , получим, что и .

Тогда элементарная работа статически приложенного момента М будет:

.

Элементарная работа внутренних сил M, Q, N будет:

.

Интегрируя dA по всей длине участка и суммируя по всем участкам стержневой системы, получим выражение полной работы внутренних сил:

.

Следует отметить, что в силу закона сохранения энергии, работа внешних сил равна работе внутренних сил:

Теоремы о взаимности работ и перемещений

Пусть к некоторой упругой стержневой системе, находящейся в равновесии, приложена статически внешняя нагрузка P1 и P2 в следующей последовательности:

1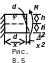 . Прикладывается статически возрастающая сила Р1 (рис. 8.6 а). В результате ее действия точка 1 (точка приложения силы Р1) получит перемещение 11. Итак, 11 – перемещение точки приложения силы Р1 по направлению ее действия от самой силы Р1. Точка 2 (точка приложения силы Р2) получит перемещение 21 – перемещение точки приложения силы Р2 по ее направлению от силы Р1.

Работа статически приложенной внешней силы Р1 будет:

2. Прикладывается статически сила Р2 (рис. 8.6 б), которая вызовет соответственно перемещения 21 и 12 точек 2 и 1 соответственно.

Работа внешней силы Р2 будет:

3. Рассмотрим случай, когда к упругой системе последовательно статически прикладываются силы Р1 и Р2 (рис. 8.7).

Из предыдущих рассмотренных случаев следует, что:

Однако сила Р2 была приложена к упругой системе, уже загруженной силой Р1, достигшей своего конечного значения. Вполне очевидно, что точка приложения силы Р1 от действия силы Р2 получит перемещение D12. Запишем работу силы Р1 на соответствующем ей перемещении:

А12 = Р1D12.

Полная работа сил Р1 и Р2 в рассматриваемом случае будет:

Изменим последовательность статического приложения внешних сил, а именно, вначале сила Р2 и затем Р1. Понятно, что точка приложения силы Р2 при приложении силы Р1 получит перемещение D21. Тогда полная работа сил Р2 и Р1 будет:

Полная работа внешних сил не зависит от последовательности их приложения, что означает:

А11 + А22 + А12 = А11 + А22 + А21, откуда:

А12 = А21.

Напомню, что А12 – работа силы Р1 (силы первого состояния) на перемещении по ее направлению D12, вызванном силой Р2 (силой второго состояния).

По аналогии можно (и нужно, но самостоятельно) дать определение работы А21.

Итак, возвращаясь к полученному результату, сформулируем теорему о взаимности работ – теорему Бетти: работа сил первого состояния на перемещениях по их направлениям от сил второго состояния равна работе сил второго состояния на перемещениях по их направлениям от сил первого состояния.

Из теоремы Бетти следует теорема о взаимности перемещений. Действительно, если Р1 = Р2 = Р, то

РD12 = Р×D21, или D12 = D21.

Если Р = 1, то 12 = 21.

П оследнее равенство носит название теоремы о взаимности перемещений (теоремы, или принципа, Максвелла): для двух единичных состояний упругой системы перемещение по направлению первой единичной силы, вызванное второй единичной силой, равно перемещению по направлению второй силы, вызванному первой силой.

Для построения теории перемещений найдем А12 через работу внутренних сил, возникающих в первом и втором состоянии.

И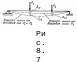 з выражения А = А11 + А22 + А12 следует, что

А12 = А – А11 – А22.

Выражение для определения полной работы легко записать, учитывая, что она может быть вызвана совместным статическим приложением нагрузок первого и второго состояния, т.е. N = N1 +N2, Q = Q1 + Q2, M = M1 + M2. Тогда

.

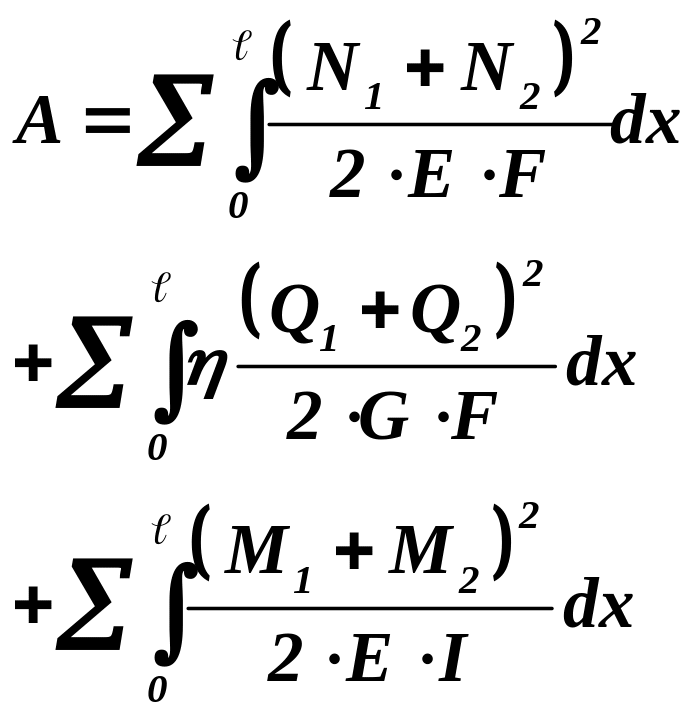Выражения для А11 и А22 получены ранее. Привожу окончательный результат определения А12 (рекомендую провести промежуточные действия самостоятельно):

.