50 Частные решения уравнения свободных колеб для систем

Т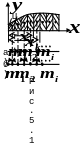 рудности динамического расчета возрастают с увеличением числа степеней свободы расчетной схемы. Реальные здания и сооружения обладают бесконечным числом степеней свободы. Как, не потеряв качество и не ошибаясь количественно, перейти к расчетной схеме, решение которой возможно. Приходится переходить к приближенным динамическим расчетам, приближенным с точки зрения выбора расчетной схемы – реальные объекты рассматривать как системы с конечным числом степеней свободы. В некоторых случаях достаточно ограничится расчетом системы с одной степенью свободы – одноэтажные многопролетные (однопролетные) рамы. При динамическом расчете балок, ферм многоэтажных рам и т.п. приходится рассматривать их как системы с несколькими степенями свободы. Если же имеется сооружение типа высотной ж/б башни (сплошной стержень), то предложены следующие способы выбора расчетной схемы (рис. 5.1).

Приближенные способы вычисления минимальной частоты колебаний

В тех случаях, когда частота колебаний вынуждающей нагрузки заведомо меньше минимальной частоты свободных колебаний, достаточно найти только ее.

1. Энергетический способ определения минимальной частоты (способ Рэлея).

По закону сохранения энергии сумма потенциальной и кинетической энергий (без учета потерь, связанных с затуханием) колеблющейся системы является величиной постоянной:

.

В каждом цикле колебаний происходит переход одного вида энергии в другой. В момент наибольшего отклонения массы от положения статического равновесия потенциальная энергия достигает наибольшего значения, а скорость и кинетическая энергия убывают до нуля (рис. 5.2).

В момент перехода масс через положение статического равновесия (рис. 5.3) потенциальная энергия убывает до нуля, а кинетическая возрастает до максимума.

Так как минимальные значения потенциальной и кинетической энергии равны нулю, то:

.

Если подставить в приведенное уравнение выражения для энергий, то получим уравнение для определения частот. При условии, что нам известна форма колебаний, т.е. вид упругой линии, то приведенное уравнение позволяет получить строгое решение.

Для получения приближенного решения зададимся видом упругой динамической линии (кривую стоячей волны) любым уравнением вида , удовлетворяющим граничным условиям. Таким уравнением может быть принято уравнение изогнутой оси стержня при действии статической нагрузки, соответствующей приложенным массам.

П отенциальную энергию деформации стержня с сосредоточенными массами выразим через работу внешних сил на соответствующих им перемещениях (рис. 5.4). , где – число масс.

Для определения максимальной кинетической энергии надо найти максимальное значение скоростей масс. Так как свободные колебания происходят по закону

, то

.

Максимальная скорость будет при , т.е.

.

Максимальное значение кинетической энергии .

Приравняв к , получим формулу для определения низшей (минимальной) частоты колебаний: , откуда .

Для балок с распределенной массой суммирование заменяется интегрированием по длине балки. В этом случае минимальная частота будет: .

Если стержень имеет постоянное сечение ), то

.

2. Определение минимальной частоты по формуле А.Ф.Смирнова.

Исходя из свойств определителя уравнений частот, профессор А.Ф.Смирнов установил пределы, между которыми заключена частота основного тона (минимальная): , где , , где

и – главные и побочные перемещения системы от действия единичных сил, приложенных в месте масс и .

3. Определение минимальной частоты по формуле С.А. Бернштейна.

Профессор С.А. Бернштейн предложил другую формулу: .

Из многочисленных численных исследований следует, что приближенные способы вычисления достаточно точно позволяют найти минимальную частоту колебаний.

5.3. Колебание системы с одной степенью свободы при действии произвольной нагрузки. Интеграл Дюамеля.

Вновь вернемся к исследованию колебаний системы с одной степенью свободы, но в данном случае внешнее воздействие является произвольно зависимым от времени . Запишем уравнение движения массы с учетом вязкого трения: , где

, .

Решение дифференциального уравнения будет состоять из суммы решений однородного уравнения и частного решения неоднородного :

.

Решение однородного уравнения нами получено ранее: , где , , .

Для получения частного решения рассмотрим вспомога­тельную задачу: найдем перемещение массы от действия на нее на­чального мгновенного импульса . Эта задача нам важна и в после­дующих исследованиях, связанных с расчетом на сейсмику.

Из теоретической механики нам известно, что импульс равен приращению количества движения, т.е.

, откуда .

Действию мгновенного импульса отвечают следующие начальные условия:При

,

.

Найдем и с учетом сформулированных начальных условий: и перепишем решение однородного уравнения: .

Примем, что действует единичный импульс, т.е. . Тогда , где называется реакцией линейного осциллятора (системы с одной степенью свободы) на единичный мгновенный импульс.

Представим произвольную нагрузку как последовательность мгновенных элементарных импульсов . Импульс по истечению времени вызовет перемещение массы, равное . Суммируя влияния всех элементарных импульсов за время от до , получим частное решение : .

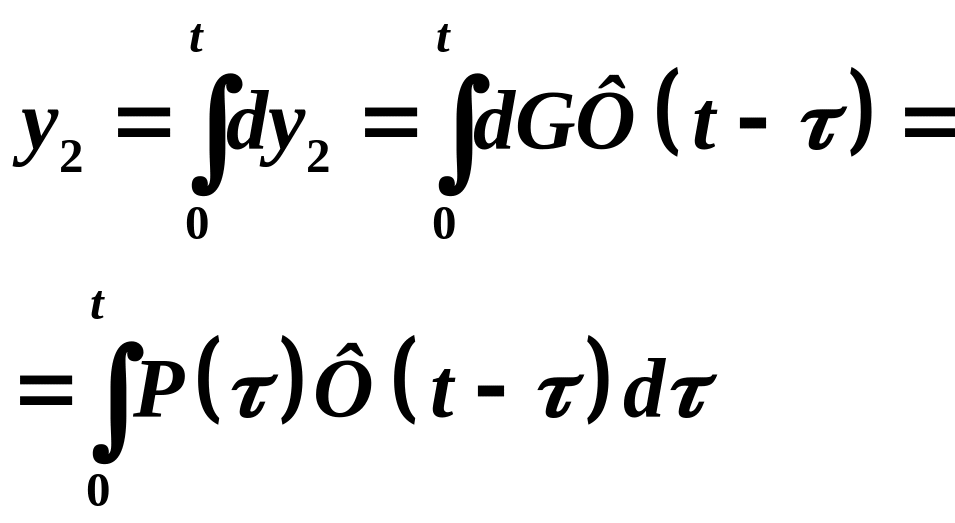Полное решение будет:

.

Это решение носит название интеграла Дюамеля.