48 Эффект резонанса

Н а рис. 2.8 показаны графики изменения динамического коэффициента при некоторых значениях неупругого сопротивление , называемые в литературе амплитудно-частотными характеристиками системы.

При совпадении частот собственных колебаний системы и вынужденных, как видно на графиках, наступает резонанс колебаний. Динамический коэффициент при будет определяться выражением: .

Так как , то при резонансе амплитуды колебаний резко возрастут, но не становятся бесконечными. Оказалось, что не смотря на относительную малость неупругих сил сопротивления, они играют важную роль при резонансных и близких к ним колебаниях. Следовательно, их учет необходим в резонансной зоне, а вне ее их влиянием можно пренебречь.

49 Свободные колебания системы с конечным числом степенени свободы.

В первом приближении, практически любое сооружение можно представить как систему с одной степенью свободы. Тогда описание ее движения сведется к одному дифференциальному уравнению, ранее нами уже исследованному. В некоторых случаях такой подход оправдан, когда достоверность работы подобной модели подтверждена другими способами – экспериментально, более точными моделями и т.д. Однако, в большинстве случаев, динамические реакции зданий и сооружений не могут адекватно быть описаны одномассовой моделью.

Р ассмотрим систему, обладающую конечным числом степеней свободы (рис. 3.1) – , поведение которой описывается соответственно независимыми параметрами перемещений каждой массы , , …, .

Пусть в некоторый момент времени система выведена внешней нагрузкой из состояния равновесия и затем совершает свободные колебания.

Перемещение любой массы в произвольный момент времени , основываясь на принципе независимости действия сил, можно представить в следующем виде:

, где

– сила инерции -й массы;

– перемещение -й массы по направлению действия инерционной силы , вызванное единичной силой инерции -й массы ( ).

С учетом того, что силы инерции для системы с степенями свободы получим следующую систему дифференциальных уравнений, описывающих движение каждой массы: ,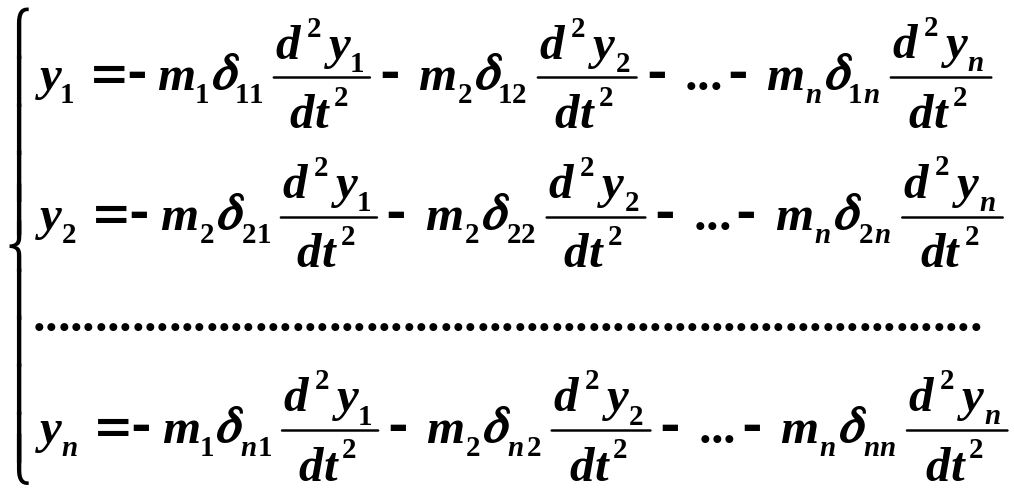

где

и вычисляются, как обычно, по формуле Мора: .

Решение полученной системы дифференциальных уравнений будем искать в виде (вспомним исследования свободных колебаний системы с одной степенью свободы без учета сил сопротивления): .

Подставив принятое решение в разрешающие дифференциальные уравнения, получим следующую систему однородных алгебраических уравнений, описывающих свободные колебания системы с степенями свободы (переходим от непрерывных параметров к дискретным): .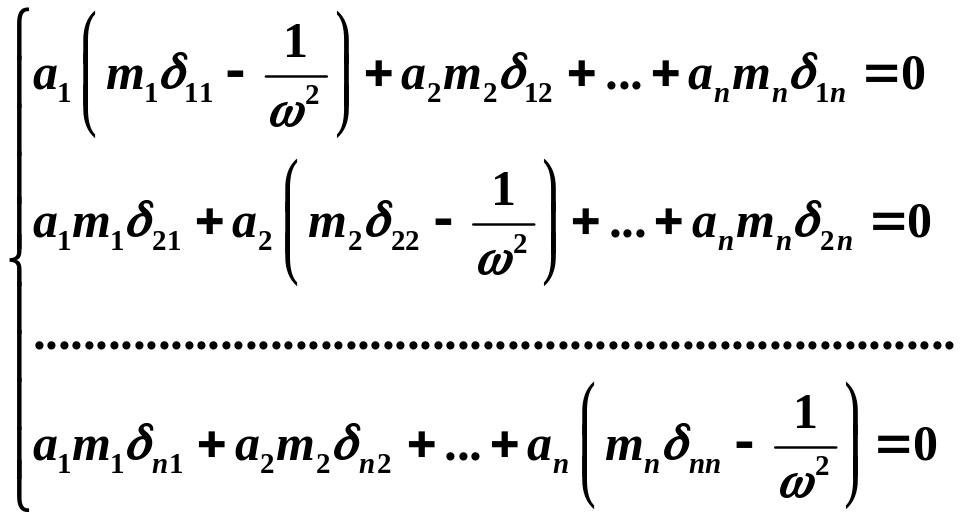

Тривиальное решение полученной системы алгебраических уравнений отвечает равенству нулю амплитуд колебаний ( ), т.е. случаю, когда система находится в покое.

Существование отличных от нуля амплитуд колебаний возможно лишь при условии равенства нулю определителя алгебраической системы уравнений, т.е.: .

Раскрыв определитель, получим уравнение частот, называемое часто в литературе вековым уравнением. Оно представляет, в общем виде, алгебраический многочлен -й степени: , где

;

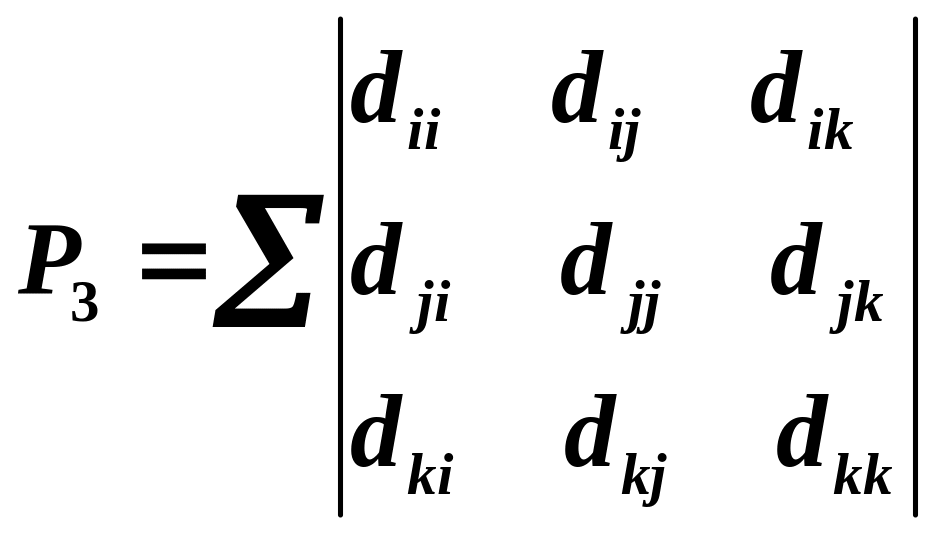– коэффициенты, определяемые как: – сумма всех диагональных элементов матрицы , где ; – сумма всех диагональных миноров второго порядка матрицы ; – сумма всех диагональных миноров третьего порядка матрицы и т.д.;

– определитель матрицы.

Корни нелинейного векового уравнения являются характеристиками частот колебаний. Сами частоты найдутся из условия:

.

Частоты, расположенные в порядке возрастания, образуют спектр частот. Каждой частоте отвечает своя форма колебаний. Для определения амплитуд колебаний , отвечающей частоте задаются любой из амплитуд, принимая ее единичной, отбрасывают одно из уравнений колебаний и получим возможность найти амплитуды колебаний с точностью до некоторого постоянного множителя.

Проверкой правильности решения задачи о свободных колебаниях системы с конечным числом степеней свободы служит условие ортогональности форм колебаний: , где

– матрица масс, ;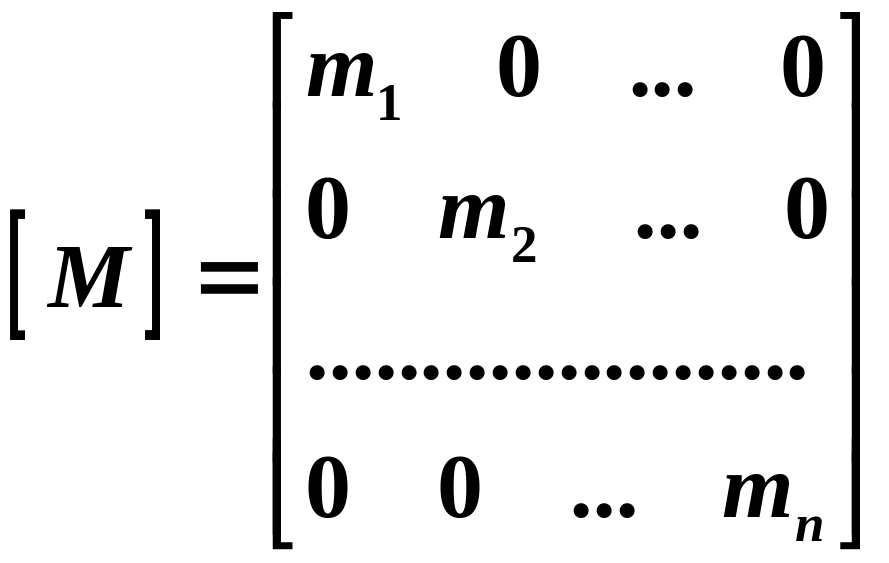

– вектор амплитуд -й формы колебаний; ;

– вектор амплитуд -й формы колебаний; .

Для практических целей часто бывает достаточно найти наименьшую частоту, представляющую наибольшую опасность с точки зрения резонанса с вибрационной нагрузкой. Низшую частоту свободных колебаний называют частотой основного тона колебаний. Следующий по порядку тон колебаний называют первым обертоном и т.д.

При или уравнение частот решается точно. При аналитическое решение затруднительно или вообще невозможно. В этом случае прибегают к численным методам определения собственных значений матрицы и собственных векторов .

Другим подходом, облегчающим решение проблемы является такой выбор независимых переменных , , …, , при котором все побочные коэффициенты . В этом случае система уравнений колебаний распадется на независимых уравнений, содержащих только главные перемещения. В этом случае , , …, называют главными координатами, а отвечающие им формы колебаний ­– главными формами колебаний.

Частоты главных форм колебаний находятся по формулам: .

Однако выбор главных координат для системы с большим числом степеней затруднителен и практикуется в основном для систем с двумя степенями свободы.