46 Колебания системы с одной степенью свободы с учетом сил сопротивления

Рассмотрим более подробно влияние сил сопротивления на свободные колебания системы с одной степенью свободы. Для этого выясним суть гипотезы В. Фойгта о вязкоупругом деформировании материала, являющейся обобщением закона Гука. В. Фойгтом закон вязкоупругости сформулирован в следующем виде: , где

– модуль упругости;

– коэффициент, характеризующий вязкость материала (размерность – время);

– скорость изменения деформации во времени.

Это соотношение можно представить как сумму упругого и вязкого напряжений:

, где и .

Очевидно, что упругое напряжение возникает в следствии действия упругой восстанавливающей силы , а вязкое – в следствии действия силы сопротивления, т.е.

, .

Запишем уравнение движения массы с учетом сил сопротивления: или , где

и .

Решение приведенного уравнения известно и имеет следующий вид: , где ­– частота затухающих свободных колебаний.

Найдем из начальных условий постоянные интегрирования и :

– при :

,

.

Тогда получим, проведя ряд преобразований, следующий вид постоянных интегрирования: ,

.

Для реальных конструкций и частоты и можно считать одинаковыми. На рис. 1.9 показан график затухающих колебаний по полученному решению уравнения движения массы .

Из анализа представленного графика движения системы с одной степенью свободы при учете сил сопротивления видно, что появление множителя приводит к затуханию гармонических колебаний и через некоторое время движение прекращается.

Важное значение в качестве характеристики свободных колебаний имеет отношение амплитуд через период колебаний :

Итак, получили что .

Эта величина обычно близка единице, поэтому в качестве количественной характеристики затухания принимают логарифм полученного соотношения: или , который называется логарифмическим декрементом затухания и определяет скорость затухания колебаний. С учетом того, что , окончательно логарифмический декремент затухания будет:

.

Как видно из полученного результата, декремент затухания, исходя из гипотезы вязкого трения, линейно зависит от частоты колебаний . С другой стороны, многочисленные эксперименты показали (рис. 1.10), что для реальных конструкций значение декремента затухания практически остается постоянной величиной, т.е. является частотно-независимой характеристикой. В указанном противоречии и суть недостатков теории Фойгта.

47 Вынужденные колебания системы с одной степенью свободы с учетом сил сопротивления при гармоническом возбуждении.

Учтем силы сопротивления колебанию по ранее рассмотренной гипотезе (В. Фойгта) условного внутреннего трения:

.

Как и ранее, вынуждающая нагрузка изменяется по синусоидальному закону: .

Уравнение движения системы с одной степенью свободы, с учетом сил сопротивления, будет: , где и .

Общее решение приведенного неоднородного дифференциального уравнения находится (ранее обсуждено), как:

, где (напоминаю), – общее решение однородного дифференциального уравнения, а – любое его частное решение.

Общее решение частного уравнения вида

хорошо известно:

, где

.

Отметим, что при .

Частным решением рассматриваемого уравнения зададимся в виде:

, или, что однозначно .

П одстановкой принятого частного решения не сложно убедится, что выбранное частное решение удовлетворяет рассматриваемому уравнению. Физически оно описывает вынужденные, т.е. установившиеся колебания упругой системы – при .

На рис. 2.7 схематично отображен график решения исследуемого дифференциального уравнения: .

Исследуем установившийся процесс более подробно.

Итак, из полученных ранее результатов, следует, что при установившимся процессе справедливо следующее решение: .

Для определения постоянных и воспользуемся следующим приемом – рассмотрим при каких и удовлетворяется искомое неоднородное дифференциальное уравнение.

Определим: ,

.

Тогда:

Отделим коэффициенты при от коэффициентов при :

Полученное уравнение может иметь решение лишь при условии, что выражения в скобках (коэффициенты при и ) равны нулю. В этом случае получим следующую систему алгебраических уравнений: .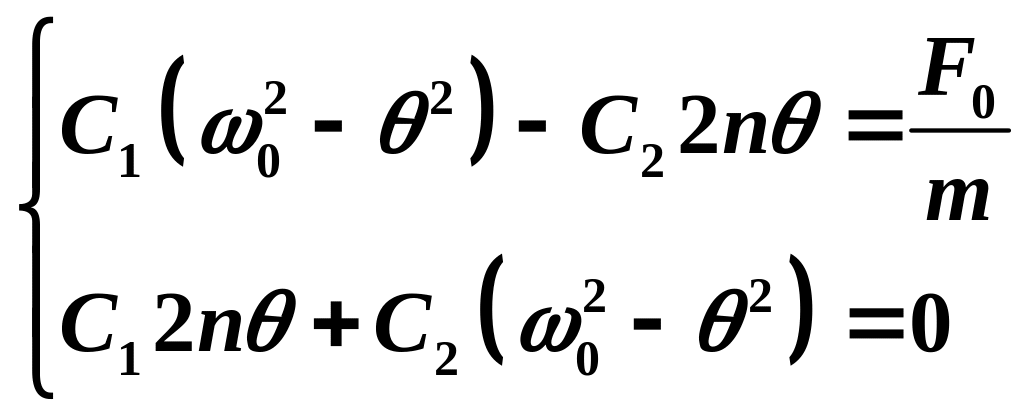

Из решения приведенной системы уравнений найдем искомые постоянные: ,

, где .

Найдем амплитуду колебаний из выражения :

.

C учетом, что тангенс угла , получим:

.

Если учтем ранее полученное выражение , то амплитуду колебаний можно перезаписать следующим образом: или .

Отношение наибольшего динамического прогиба к статическому прогибу ранее было определено как динамический коэффициент . С учетом, что и , получим следующее выражение для динамического коэффициента : .