34 Статич метод.

Рассмотрим абсолютно жесткий невесомый стержень длиной , закрепленный в основании упругоподатливой связью относительно поворота (рис. 1.10). Жесткость опорной связи, т.е. величина опорного момента при повороте стержня на угол , обозначим k. На стержень со стороны незакрепленного торца действует вертикальная сила P. Требуется найти минимальное значение Р_кр, при котором стержень потеряет устойчивость.

Составим уравнение равновесия в виде равенства нулю суммы моментов всех сил, действующих на предполагаемую деформированную схему, относительно опоры: .

С учетом, что , запишем . (1.1)

Так как угол мал в силу того, что отклонения системы от первоначального положения малы, то и .

Окончательно уравнение равновесие примет следующий вид: .

Последнее уравнение называется уравнением устойчивости. Его анализ дает два решения: .

Первое говорит о том, что система при любом значении силы Р может находиться в недеформированном состоянии.

И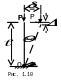 з второго решения следует, что при достижении возможно деформированное состояние системы, характеризуемое некоторым углом . Однако величину угла не представляется возможным найти, так как использовалось линеаризованное уравнение равновесия. Подобный случай характерен для всех решений, полученных на основе линейных соотношений нагрузок и перемещений.

Полный анализ поведения стержня требует решения нелинейного уравнения (1.1). Для большинства реальных задач получить точное решение нелинейного уравнения не удается. Однако, как правило, в задачах устойчивости основной проблемой является установление величины критической нагрузки, поведение системы в закритическом состоянии представляет меньший интерес.

35 Динамический и энергетич. Методы.

Решим рассмотренную ранее задачу энергетическим методом. Составим выражение полной энергии упругой системы при переходе ее в деформированное состояние. Полную энергию упругой системы найдем как сумму работ внешней силы Р и внутренней – опорной реакции.

В процессе деформирования величина силы Р остается постоянной и ее работа определится выражением:

.

Найдем .

В силу малости перемещений можно положить, что , тогда .

Окончательно работа внешней силы:

.

Работа момента , возникающего в упругой связи, будет (реактивный момент возрастает от нуля до конечного значения): .

Величина полной энергии упругой системы в деформированном состоянии: .

Равновесное состояние будет тогда, когда , т.е. ,

или . Тогда .

Видим, что полученное решение совпало с результатом статического метода.

Энергетический метод позволяет провести и дальнейшие исследования. Для этого используется вторая вариация полной энергии: .

В устойчивом состоянии , т.е. .

В безразличном, т.е. критическом состоянии , тогда

.

В закритическом состоянии , .

динамическим методом

Возможное движение жесткого стержня с податливой упругой опорой (рис. 1.10) характеризуется поворотом стержня относительно точки О.

Уравнение движения при вращении имеет следующий вид: ,

где I – момент инерции массы стержня относительно точки О.

Для рассматриваемого случая . Тогда уравнение движения будет: или .

Получили нелинейное дифференциальное уравнение, так как имеется слагаемое, содержащее . Исследование такого уравнения – задача не из простых, поэтому воспользуемся линеаризацией уравнения. Согласно доказательству А.М.Ляпунова, для систем с конечным числом степеней свободы можно решать задачу устойчивости путем исследования соответствующих линеаризованных уравнений.

В нашем случае примем, что и уравнение движения примет вид: или .

Обозначим , тогда: .

Решение полученного дифференциального уравнения известно (ранее встречалось в курсе теоретической механики): , где

– угол, характеризующий наибольшее отклонение стержня (амплитуда);

– угол сдвига фазы колебаний.

Анализ решения приводит к выводу, что стержень при любом конечном значении спустя некоторый период времени вернется в исходное положение и будет совершать незатухающие колебания относительно положения равновесия, так как не учтены силы сопротивления колебаниям. Период этих колебании определяется известным выражением: .

В случае, когда период неограниченно велик, т.е. стремится к бесконечности, система, выведенная из состояния устойчивого равновесия, практически в него не вернется. Очевидно, что период колебаний Т будет стремиться к бесконечности лишь в случае, когда частота стремится к нулю. В пределе это позволяет записать, что , откуда находим критическую силу .

Итак, результаты решения одной и той же задачи тремя различными методами совпали. Такое возможно не всегда, так как только динамический метод является универсальным, а другие в более сложных задачах дадут лишь приближенные результаты.