8 Распорные системы опред опорных реак и усилия в 3-ёх шарн арках рачиональная схема 3-ёх шарн арки.
Трехшарнирная система – система жестких дисков, образованная из трех дисков (один из которых – основание), связанных между собой шарнирами (рис. 5.1).
Р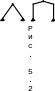
азличают
следующие основные типы трехшарнирных
(распорных) систем:
1. Если в трехшарнирной системе два диска являются
прямолинейными или ломанными стержнями, то такая конструкция называется трехшарнирной рамой (рис. 5.2).
2. Если в трехшарнирной системе два диска являются сквозными решетчатыми конструкциями, то такая система называется трехшарнирной арочной фермой (рис. 5.3).
3. Арки – сооружения, у которых два диска представляют собой криволинейные стержни, оси которых описаны аналитически или заданы таблично (рис. 5.4).
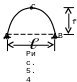
Расстояние между
опорами
называют пролетом арки, а расстояние
от шарнира С до прямой, соединяющей
опоры – f – стрелой подъема арки. Иногда
шарнир С называют ключом (замком) арки,
а опорные шарниры – пятовыми или пятами
арки.
В общем случае трехшарнирные системы могут быть как симметричные, так и несимметричные.
Разновидностями трехшарнирных систем могут быть системы с затяжками (рис. 5.5).
Различные типы трехшарнирных систем нашли широкое применение в мостостроении, сельском строительстве, при перекрытии больших пролетов промышленных цехов, зрелищных сооружений, где они являются экономичными и надежными.
Определение внутренних усилий в трехшарнирной арке
Рассмотрим арку загруженную вертикальной нагрузкой (рис. 5.6). Найдем внутренние усилия в нектором сечении, положение которого определено координатами и y (рис. 5.6). Рассмотрим равновесие левой отсеченной части (рис. 5.7).
Определим внутренние усилия в сечении с известными координатами x и y из следующих условий равновесия рассматриваемой отсеченной левой части арки:
Найдем изгибающий момент Mx:
,
откуда
.
Обратим внимание на то, что выражение
отвечает изгибающему
моменту в сечении x в эквивалентной
балке (рис. 5.7).
Окончательно
.
Из полученной формулы следует, что изгибающий момент в арке меньше, чем в эквивалентной балке.
Найдем поперечную
силу
:
,
откуда, с учетом,
что
– поперечная силав сечении x в эквивалентной
балке, получим:
.
Отметим, что поперечная сила в арке меньше, чем в аналогичной балке.
Нормальную силу в
сечении x определим из условия равновесия
в виде равенства нулю проекций всех сил
слева от сечения на ось
:
.
Как видно из полученного выражения, в арке нормальная сила сжимающая и хотя ее величина возрастает по сравнению с поперечной силой в аналогичной балке, но большинство строительных материалов хорошо работают на сжатие, чего не скажешь о растяжении.
Расчет арки обычно ведется следующим образом:
– арка мысленно разбивается на ряд участков, чтобы в сечения обязательно попали сосредоточенные силы и дополнительные, так как эпюры внутренних сил в при любой нагрузке криволинейны. Следует предусмотреть достаточное количество сечений для достижения точности расчета;
– расчет ведется в табличной форме, форма таблицы будет показана на практических занятиях.
Понятие о рациональной оси арки
Рациональной осью арки называется такое ее очертание, когда изгибающий момент во всех сечениях равен нулю.
В силу определения рациональной оси арки положим, что
.
Проведем элементарные преобразования:
.
Полученное выражение утверждает, что для того, чтобы ось арки была рациональной, закон ее изменения должен отвечать закону изменения балочного изгибающего момента.
Примером рациональной оси арки является параболическая кривая, если на арку действует равномерно распределенная нагрузка:
.
По такой формуле следует принять закон изменения оси арки при расчете ее в контрольной работе.