43 Методы решения динам задач.Статич,энергетич.

Основными методами динамического расчета являются статический и энергетический.

Статический метод основан на применении уравнений динамического равновесия, которые отличаются от уравнений статического равновесия наличием дополнительных сил инерции.

Энергетический метод основан на законе сохранения энергии: сумма потенциальной и кинетической энергии упругой системы является величиной постоянной в любой рассматриваемый момент времени.

Трудоемкость динамического расчета сооружений зависит, в первую очередь, от числа степеней свободы.

44 Диф урав-ия системы с однои степ свободы.

Р ассмотрим систему с одной степенью свободы (рис. 1.5). Если к ней приложена статическая нагрузка , то балка изогнется и масса сместиться на .

К огда же к массе приложена некоторая сила , переменная во времени, то система будет совершать колебательные движения относительно устойчивого положения равновесия (рис. 1.6).

Р ассмотрим характер сил, действующих на систему в любой момент времени (рис. 1.7), где

– сила инерции; нам известно, что она определяется величиной массы и ее ускорением:

,

 – независимый пара­метр, определяющий поло­жение массы в любой момент времени;

– восстанавливаю­щая сила, отражающая упругие свойства системы, принято считать, что

, – реакция системы при единичном смещении;

Для рассматриваемого случая коэффициент определиться из выражения:

, где – перемещение балки в месте расположения массы от силы . Тогда

и .

– сила сопротивления, при этом различаем силы внутреннего сопротивления (внутреннее трение), связанные со свойствами материала и силы внешнего сопротивления – сопротивление окружающей среды. Единой теории, описывающей внутреннее сопротивление не существует, в ряде случаев оказывается пригодной теория Вольдемара Фойгта (1850-1919 гг.), по которой, в упрощенном виде, можно принять, что

, – коэффициент вязкости материала.

Запишем условие динамического равновесия системы: или

.

Запишем в более удобном виде: .

Исследуем некоторые частные случаи колебания системы с одной степенью свободы.

45 Свобою колеб. Системы с однои степ свободы.

Напомню, что свободными колебаниями системы называются такие, которые происходят при отсутствии внешней нагрузки – возмущающей силы. Другими словами, к упругой системе в какой-то период времени была приложена возмущающая нагрузка , система была выведена из состояния равновесия, а затем действие нагрузки прекратилось. В этом случае упругая система будет продолжаться колебаться относительно первоначального положения равновесия.

Предположим, что силы сопротивления настолько малы, что ими можно пренебречь, т.е. , что отвечает, естественно только идеально упругой системе.

Уравнение динамического равновесия, с учетом высказанных выше предположений, примет следующий вид:

или

, где .

Пришли к обыкновенному дифференциальному уравнению второго порядка с постоянными коэффициентами, решение которого хорошо известно (Э. Камке. Справочник по обыкновенным дифференциальным уравнениям. М. Наука, 1971, стр.365): .

Постоянные интегрирования найдем из начальные условий (условий при ):

Тогда: , откуда ; , откуда .

Окончательно решение имеет следующий вид: .

Полученное решение описывает простое гармоническое движение.

Более наглядное представление о характере колебаний можно получить, если перейти к другим константам интегрирования ( и ), следующим образом связанных с :

, или , .

Тогда решение запишется в следующем виде: .

Принято называть:

– амплитуда колебаний, т.е. максимальное отклонение колеблющейся массы от положения статического равновесия;

– начальный угол сдвига фазы колебаний;

– круговая или угловая частота колебаний, рад/сек.

Оказалось удобным ввести еще ряд характеристик колебаний:

– период колебаний, т.е. время одного колебания, , так как период тригонометрических функций равен ;

– техническая частота колебаний, определяет число колебаний в секунду.

На рис. 1.8 показаны основные элементы гармонических свободных незатухающих колебаний.

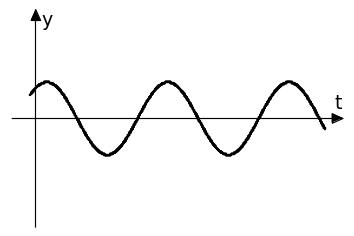
Свободные колебания системы с одной степенью свободы являются собственными колебаниями, т.е. периодическими колебаниями по гармоническому закону с одной частотой, форма колебаний, ей отвечающая, называется собственной или главной формой колебаний.

Запишем выражения для частот и периодов собственных колебаний, имея в виду, что , где – ускорение свободного падения.

Круговая частота .

Обозначим и тогда получим, что .

Период колебаний: /

Техническая частота: .

Частота и период представляют собой основные динамические характеристики системы. Это связано с тем, что для системы с одной степенью свободы, как видно, эти характеристики не зависят от начальных условий, в то время, как амплитуда колебаний и начальный сдвиг фазы колебаний зависят от них.

Очевидно, что исследование незатухающего процесса колебаний дает лишь приближенное представление о реальной работе системы с одной степенью свободы. В любой упругой среде происходит поглощение-рассеивание энергии.