40 Устоич стержня в упругои среде
Рассмотрим сжатый
стержень на двух шарнирных опорах,
лежащий на упругом основании с
коэффициентом постели
(рис. 3.1). Такая расчетная схема основана
на гипотезе Фусса–Винклера.
З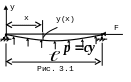
апишем
дифференциальное уравнение изогнутой
оси стержня:
,
где
– изгибающий момент
от сил (реакции) упругого основания.
Продифференцируем его дважды:
,
так как
,
то, приняв во внимание, что
,
окончательно получим:
Решение полученного
дифференциального уравнения будем
искать в виде тригонометрического
ряда:
.
Обратим, что функции
удовлетворяют граничным условиям.
Найдем вторую и
четвертую производные от
:
Подставим в
разрешающее дифференциальное уравнение: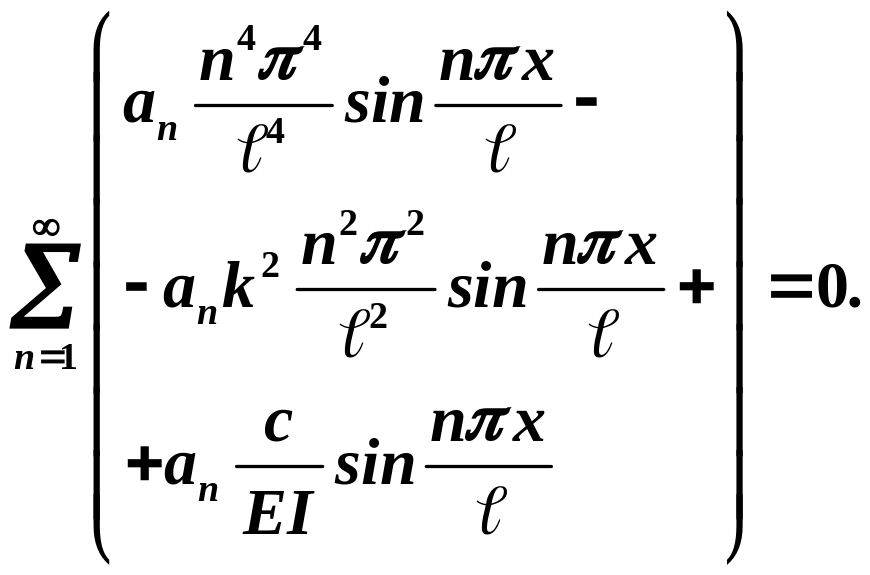
Преобразуем его к
более удобному для анализа виду:
Каждое слагаемое
полученного ряда должно равняться
нулю: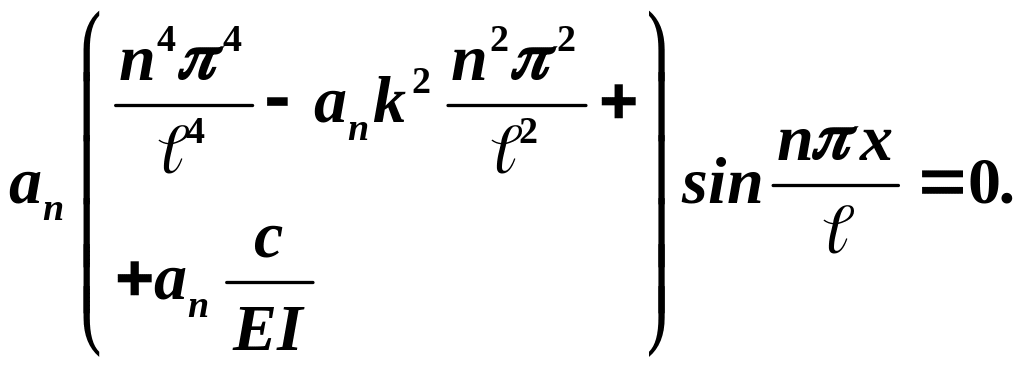
Так как
и
при любых
не равны нулю, то
.
Из полученного
уравнения найдем искомую критическую
силу
:
.
Приняв, что
,
а
,
окончательно получим:
.
Параметр
определяет количество полуволн
искривленной оси стержня. Определим
,
соответствующее наименьшей критической
силе. Примем, что
меняется непрерывно. Тогда
,
откуда
и
.
Из полученной
формулы следует, что
может быть любым числом, а не только
целым. В случае, если
окажется не целым числом, то для нахождения
критической силы
необходимо проверить два ближайших
целых значения
.
Наименьшую критическую силу примем за
истинную. Однако, в частном случае, может
оказаться, что обе силы одинаковы. Так,
если
,
то
.
Найдем критические силы при
и
:
– при
;
– при
.
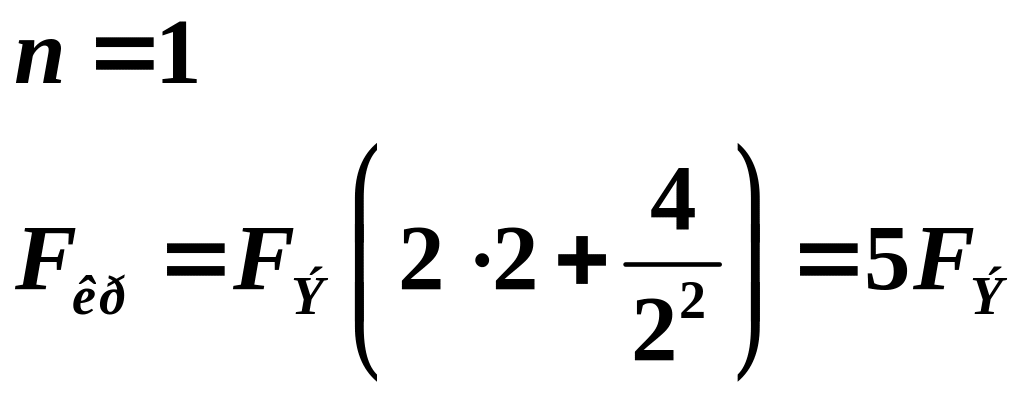41 Устоичивость форм равновесия при чистом изгибе.
Р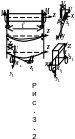
ассмотрим
балку прямоугольного сечения с таким
закреплением торцов, при котором возможны
лишь перемещения их в вертикальной
плоскости (3.2). Балка загружена на опорах
сосредоточенными моментами. В
деформированном состоянии произвольное
сечение (рис. 3.2) сместится по вертикали
на
,
по горизонтали – на
и повернется на угол
.Определим,
с точностью до бесконечно малых первого
порядка, изгибающие моменты относительно
принятых координатных осей: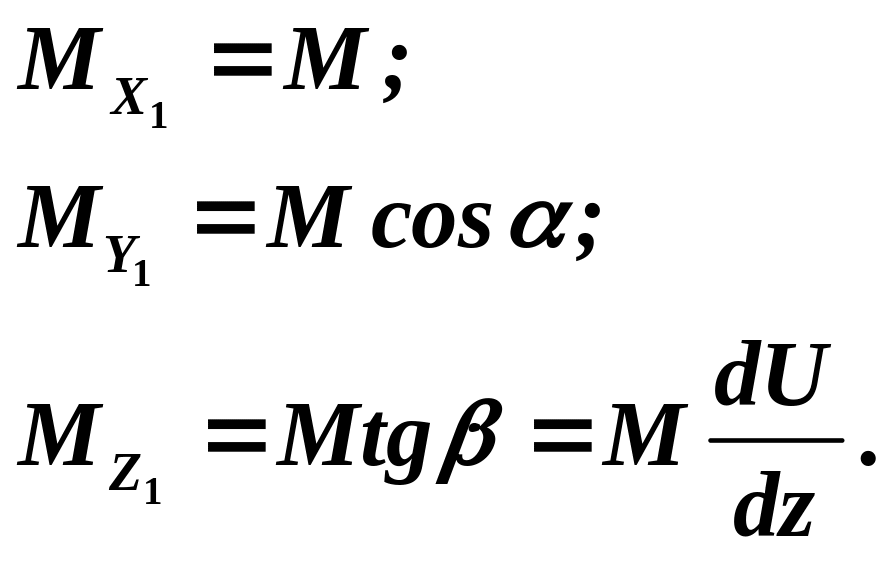
Запишем
дифференциальные уравнения кручения
и изгиба в двух плоскостях: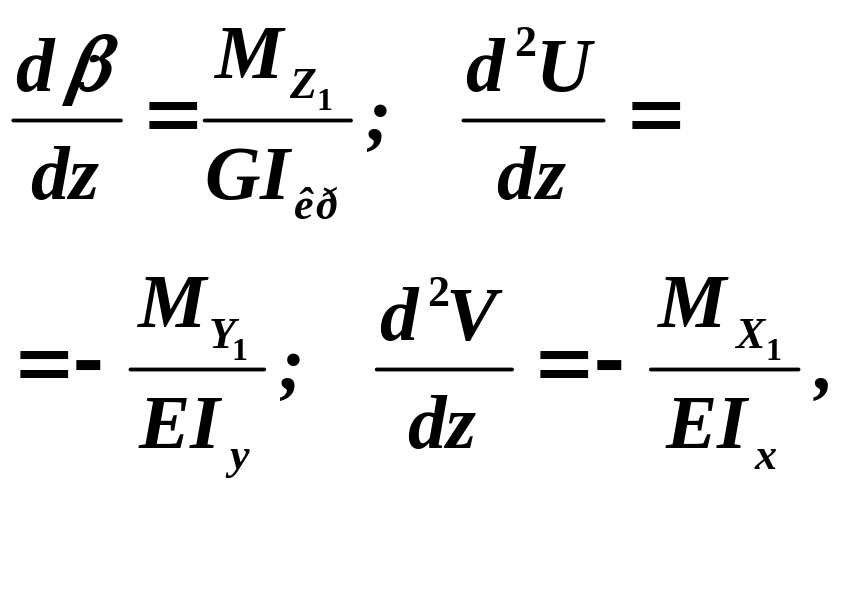
где
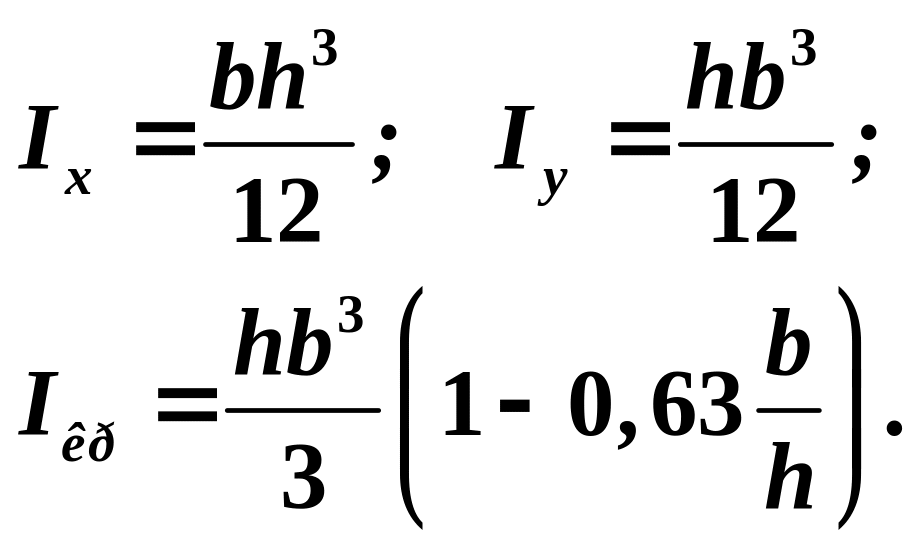
С учетом малости
углов
и
,
получим: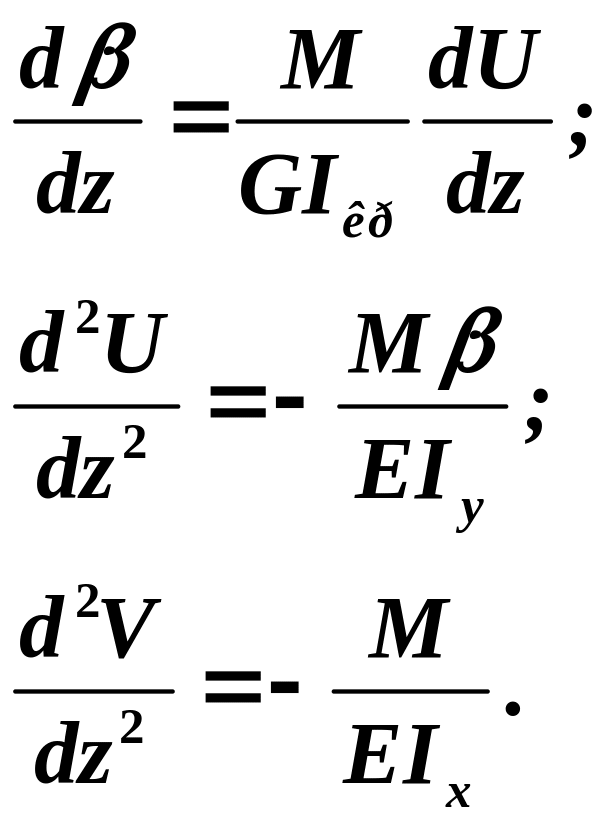
Дифференцируя
первое уравнение по
:
и учитывая второе
(
),
получим:
где
Решение полученного
дифференциального уравнения:
Из граничных условий найдем постоянные и :
– при
и
– при
и
Так как при
не произойдет выпучивания стенки балки,
то нас интересует случай, когда
:
или
,
откуда:
Нас интересует,
естественно, наименьший критический
момент (
):
Если концы балки
защемлены, то, упуская промежуточные
выкладки, получим:
42 Динамич нагр.Св-ва классиф. Степень динамич свободы.
Динамическими нагрузками называются такие, которые во время действия сообщают массам сооружения ускорения, вызывая тем самым инерционные силы.
Виды динамических нагрузок
Динамические нагрузки по своей природе многообразны и в основном сводятся к следующим:
1. Периодическая нагрузка – повторная нагрузка, для которой существует один и тот же период повторения при большом числе циклов.
Наиболее простая периодическая нагрузка – синусоидальная (рис. 1.1), называемая простой гармоникой. Такие нагрузки характерны для вибрационных машин с неуравновешенными массами.
Другие виды периодических нагрузок более сложные, например, гидродинамическое давление от винтов корабля (рис. 1.2). Однако с помощью разложения в ряды Фурье любая периодическая нагрузка может быть представлена в виде суммы простых гармонических составляющих.
2. Кратковременная нагрузка (импульсы) характерна быстрым развитием и быстрым исчезновением, т.е. почти мгновенным действием. Такую нагрузку создают взрывы (рис. 1.3).
3. Ударная нагрузка – удары в определенном месте сооружения. Характерна резким изменением скорости ударяемого тела в малый промежуток времени. Такая нагрузка может быть и периодической. Ее создают падающие тела, всевозможные копры, молоты и т.п.
4. Подвижная нагрузка постоянного или переменного значения, изменяющая свое положение, например, подвижный транспорт.
5. Сейсмическая нагрузка (рис. 1.4). Характерна беспорядочным движением почвы, толчками, ударами и колебаниями при землетрясении.
Динамический расчет сооружений отличается от статического двумя важными моментами.
Основными методами динамического расчета являются статический и энергетический.
Статический метод основан на применении уравнений динамического равновесия, которые отличаются от уравнений статического равновесия наличием дополнительных сил инерции.
Энергетический метод основан на законе сохранения энергии: сумма потенциальной и кинетической энергии упругой системы является величиной постоянной в любой рассматриваемый момент времени.
Трудоемкость динамического расчета сооружений зависит, в первую очередь, от числа степеней свободы.
Числом степеней свободы сооружения называется число независимых геометрических параметров, определяющих его положение в любой момент времени.
Реальные сооружения обладают бесконечным числом степеней свободы.