20 Методы устранения лишних связей.

Основная система должна быть такой, чтобы:

Обеспечивалась простота построения эпюр Mi и MP.

Объем вычислений был минимален при определении коэффициентов ij и iP.

Часть или все побочные коэффициенты канонических уравнений равнялись нулю: ij = 0 (i ≠ j), что существенно упростит решение системы канонических уравнений.

Основная система метода сил, удовлетворяющая всем или части перечисленных требований (при невозможности другого), называется рациональной основной системой.

Рассмотрим некоторые приемы, позволяющие упростить выбор рациональной основной системе метода сил.

1. Способ замкнутых сечений

Степень статической неопре­делимости будет:

W = 3K – Ш = 3∙3 – 0 = 9, или

W = 2∙Ш + Со – 3∙Д = 12 – 3 = 9

Если принять за основную сис­тему статически определимую раму, полученную путем замены «лишних» связей в виде опорных реакций (рис. 2.2 а), то все коэффициенты ij ≠ 0 и придется решать

полную систему алгебраических уравнений.

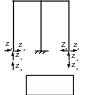
Иная картина будет, если применить способ замкнутых сечений, в основе которого лежит рассечение системы на отдельные самостоятельные части (рис. 2.2 б). В этом случае «лишними» усилиями являются внутренние усилия и часть коэффициентов d_ij = 0, а именно:

₁₇ = ₇₁ = 0; ₁₈ = ₈₁ = 0; ₁₉ = ₉₁ = 0;

₂₇ = ₇₂ =0; ₂₈ = ₈₂ = 0; ₂₉ = ₉₂ = 0;

₃₇ = ₇₃ = 0; ₃₈ = ₈₃ = 0; ₃₉ = ₉₃ = 0.

Естественно, при выборе такой основной системы упроститься построение эпюр, уменьшится объем вычислений и легче будет решить систему канонических уравнений.

Способ группировки неизвестных

Е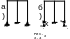 сли статически неопределимая рама симметрична, но не все опоры являются жесткими (рис. 2.4 а), то применить для выбора основной системы способ замкнутых сечений невозможно. В любом случае в качестве неизвестных усилий войдут опорные реакции (рис. 2.4.б). Основную систему можно выбрать симметричной, но только в отношении геометрии. еизвестные усилия не будут симметричны и, конечно, все коэффициенты канонических уравнений d_ij будут отличны от нуля. Проблема: а нельзя ли представить неизвестные усилия каким-то образом симметричными и кососимметричными в нашем конкретном случае? Оказывается можно однозначно решить данную задачу. Действительно, перейдем к другим неизвестным усилиям путем разложения неизвестных х_i на симметричные и кососимметричные (рис. 2.5). Правомочность разложения следует из однозначности определения новых неизвестных z_i из решения следующих систем алгебраических уравнений:

,

.

Из новых неизвестных z_i осесимметричны z₁ и z₃, а кососимметричны z₂ и z₄. Так как

, то

.

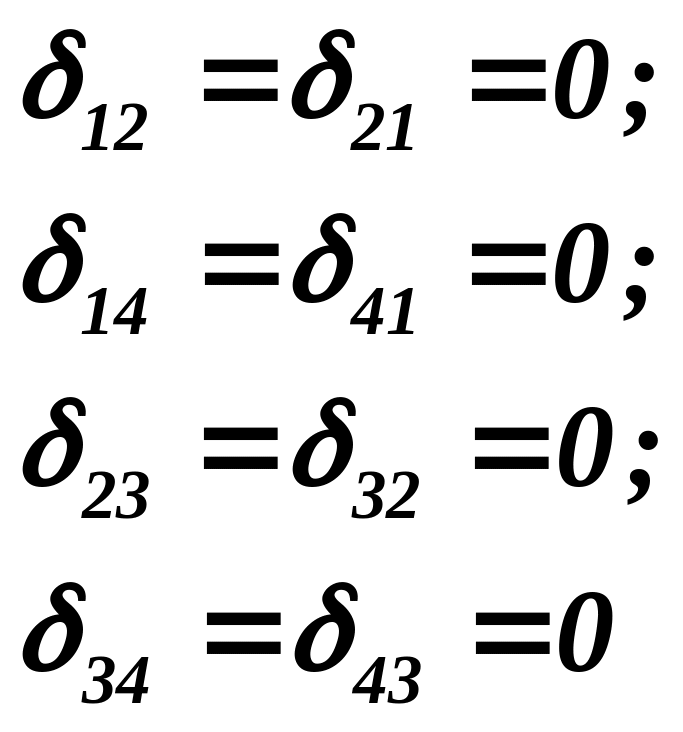Система канонических уравнений распадется на две – с симметричными и кососимметричными неизвестными:

,

.

Таким образом, группировка неизвестных не только сокращает объем вычислений, но и упрощает систему канонических уравнений – она распадается на две, что упрощает решение.

Способ разложения внешней нагрузки на симметричную и кососимметричную

Способ группировки особенно эффективен при одновременном разложении по тому же принципу внешней нагрузки на симметричную и кососимметричную.

Разложение нагрузки на симметричную и кососимметричную упростит построение эпюр и вычисление свободных членов _iP. Принцип разложения внешней нагрузки легко понять из рис

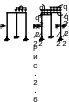К сожалению, способы, упрощающие вычисление коэффициентов и решение канонических уравнений метода сил относятся в большей мере к симметричным рамам. В отношении несимметричных рам можно посоветовать следующее – стремитесь выбрать, а для этого надо иметь не одну, основную систему, в которой общее количество участков в эпюрах от единичных неизвестных было минимальным, что упростит вычисления.