Тема 1 «Метод прямоугольного треугольника»

Задачи по теме 1 выдаются на первой неделе. Знаний, полученных при прослушивании лекции 1 и усвоенных на практическом занятии 1, достаточно для решения задач. Из теоретического материала необходимо освоить метод нахождения натуральной величины отрезка методом прямоугольного треугольника [1, 2, 3].

1.1 Теория к выполнению индивидуального задания «Определение угла наклона прямой общего положения к плоскостям проекций. Истинная величина отрезка»

Угол между прямой и плоскостью проекций ‑ это угол между прямой и ее проекцией на эту плоскость.

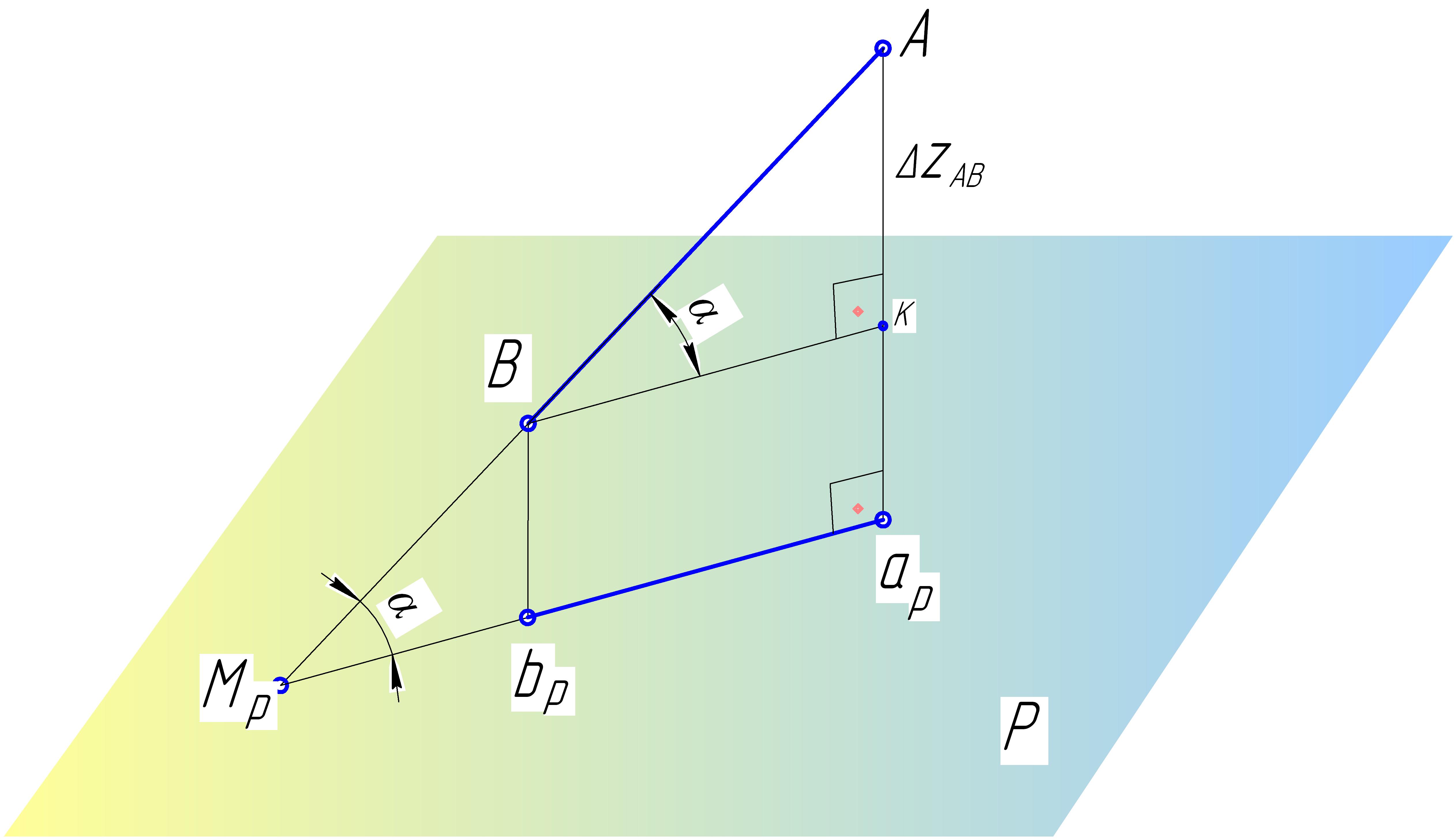
Рисунок 1 ‑ Положение прямой АВ относительно плоскости Р

На рисунке 1 изображена в пространстве некоторая плоскость проекций Р и отрезок прямой АВ:

а_рв_р ‑ проекция отрезка АВ на плоскость Р;

 ‑ угол между отрезком АВ и плоскостью проекций Р.

Проведя ВК параллельно а_рв_р, видим, что угол  может быть определен из прямоугольного треугольника, одним катетом которого является проекция прямой на эту плоскость, а другим ‑ разность расстояний концов отрезка (ВК = Аа_р ‑ Вb_р) до данной плоскости проекций (ΔΖ).

Следовательно, для того чтобы определить на эпюре угол между прямой и плоскостью проекций Н (угол ), надо на горизонтальной проекции a₁b₁ этой прямой, как на катете (рисунок 2), построить прямоугольный треугольник. Вторым катетом будет отрезок b₁Во, равный разности расстояний концов отрезка АВ от плоскости Н (ΔΖ). При этом гипотенуза а₁В_0, построенного треугольника, равна истинной величине отрезка АВ. Прямоугольный треугольник можно размещать в любом месте поля чертежа.

Рисунок 2 ‑ Определение натуральной величины отрезка АВ

и угла его наклона к плоскости Н

Аналогично, для нахождения угла между прямой и плоскостью проекций V (угла ) на фронтальной проекции прямой, как на катете (рисунок 3), построить прямоугольный треугольник, вторым катетом которого будет разность расстояний концов отрезка от плоскости V (ΔΥ).

Гипотенуза a₂B₀ построенного треугольника ‑ истинная величина отрезка АВ.

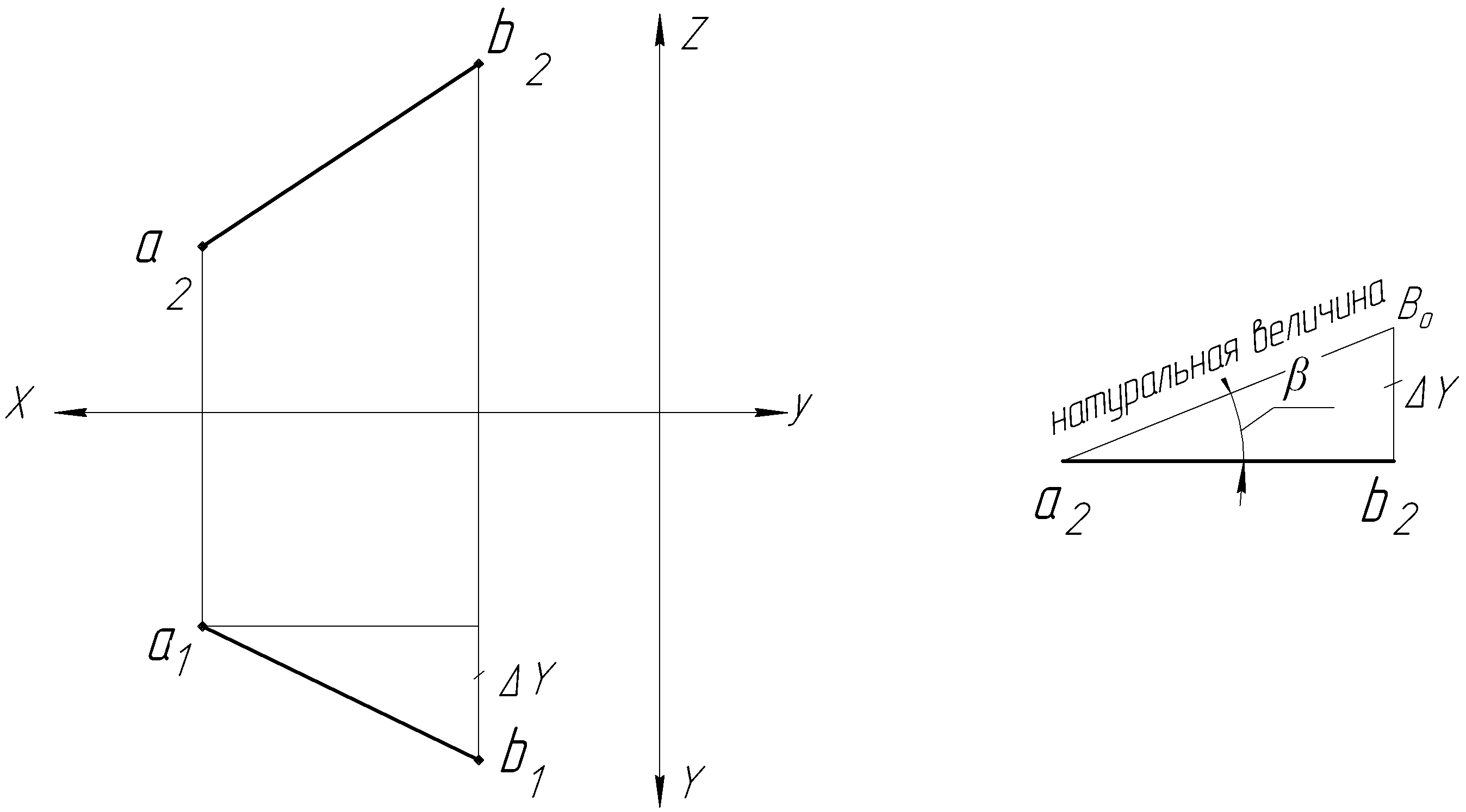
Рисунок 3 ‑ Определение натуральной величины отрезка АВ

и угла его наклона к плоскости V

Чтобы найти угол γ (угол наклона отрезка к профильной плоскости W), используйте профильную проекцию а₃в₃ и разность координат ΔΧ (рисунок 4).

1.2 Оформление задачи на формате

Чертеж оформляется на формате А4. Вычерчивается рамка и место для основной надписи стилем линий Основная.

Постройте по координатам отрезок АВ (три проекции). Обозначьте горизонтальную, фронтальную и профильную проекции отрезка соответствующими буквами и индексами. Отметьте значения ΔΖ, ΔΧ и ΔΥ.

Используйте их при построении прямоугольных треугольников.

Заполните основную надпись чертежным шрифтом № 5.

Рисунок 4 ‑ Пример оформления на формате А4 задачи 1 по теме1

Тема 2 «Прямые и точки, принадлежащие плоскости»

Задачи по теме 2 выдаются на второй неделе, после проведения практического занятия 2, с учетом знаний, полученных на лекции 1 [1, 2, 3, 4, 5].

Для решения задач необходимо усвоить следующий теоретический материал:

а) частное и общее положение прямых;

б) частное и общее положение плоскостей;

в) условия принадлежности точки и прямой плоскости;

г) условия параллельности прямой и плоскости.