8.1.4 Построение развертки прямого конуса

Рассмотрим построение развертки конуса. Несмотря на то, что конические поверхности являются развертывающимися и, следовательно, имеют теоретически точные развертки, практически строят их приближенные развертки, пользуясь способом треугольников. Для этого заменяют коническую поверхность вписанной в нее поверхностью пирамиды.

Построим развертку прямого конуса с отсеченной вершиной (рисунок 55).

Необходимо предварительно построить развертку боковой поверхности конуса. Этой разверткой является круговой сектор, радиус которого равен натуральной величине образующей конуса, а длина дуги равна длине окружности основания конуса. Практически дугу сектора определяют при помощи ее хорд, которые принимают равными хордам, стягивающим дуги основания конуса. Иначе говоря, поверхность конуса заменяется поверхностью вписанной пирамиды.

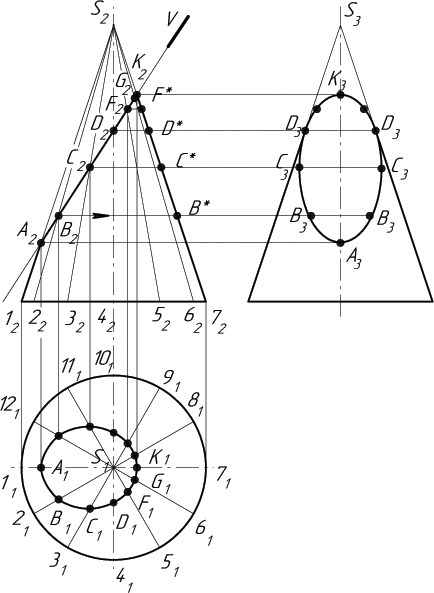
Рисунок 55 – Сечение конуса фронтально проецирующей плоскостью

Чтобы на развертку (рисунок 56) нанести точки фигуры сечения (А,В,С,D,F,G,K), нужно предварительно определить их натуральные расстояния от вершины S, для чего следует перенести точки А₂, В₂, С₂, D₂, F₂, G₂, K₂ на соответствующие натуральные величины образующих конуса. Так как в прямом конусе все образующие равны, то достаточно перенести проекции точек сечения на крайние образующие S₂1₂ и S₂7₂. Таким образом, отрезки S₂A*, S₂B*, S₂D*, S₂F*, S₂G*, S₂K* являются искомыми, т.е. равными натуральной величине расстояния от S до точек сечения.

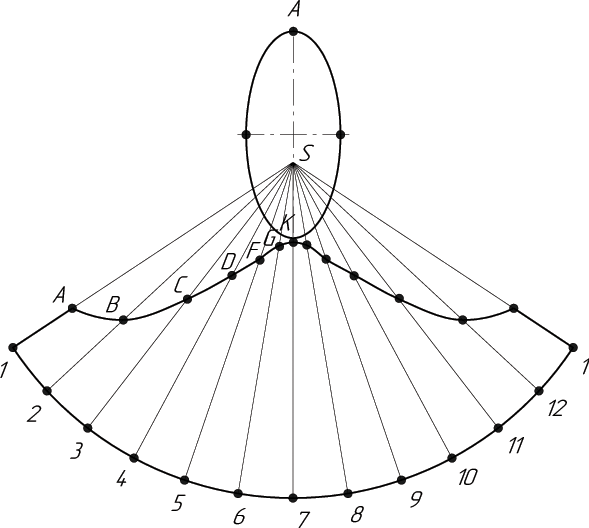
Рисунок 56 – Развертка прямого конуса

8.1.5 Сечение прямого кругового конуса плоскостями общего положения

При решении задачи сделайте преобразование чертежа, превратив плоскость Р в проецирующую (рисунок 57). Новую ось X₁ проведите перпендикулярно горизонтальному следу Рн. Произвольную точку на фронтальном следе Рv спроецируйте на новую плоскость проекций. На новой плоскости проекций обозначьте след плоскости Р как след Р_V1. Плоскость Р стала проецирующей, и фигура сечения заключена между проекциями точек 1₄-2₄-3₄-4₄-5₄-6₄. По линиям связи перенесите точки фигуры сечения на горизонтальную и фронтальную плоскости проекций. Найденные точки 1 и 2 являются высшей и низшей точками сечения и большой осью эллипса. Крайние точки видимости для фронтальной проекции (левую и правую точки 4 и 3) находим по построению: построим образующие, на которых они находятся на третьей проекции. Обозначим их 3₄-4₄ и перенесем по линиям связи на горизонтальную проекцию 3₁-4₁. Затем находим по линиям связи их положение на фронтальной проекции. Точки 5 и 6 лежат на окружности, проведенной через середину отрезка 1₄-2₄, на плоскости проекций Т₄ и являются малой осью эллипса. Все найденные точки сечения являются опорными, т.е. обязательными к построению.

Чтобы нанести точки фигуры сечения на развертку, обязательно найдите натуральную величину их положения на образующих. Для этого спроецируйте каждую точку на крайнюю образующую конуса (например, как точка 5^х).

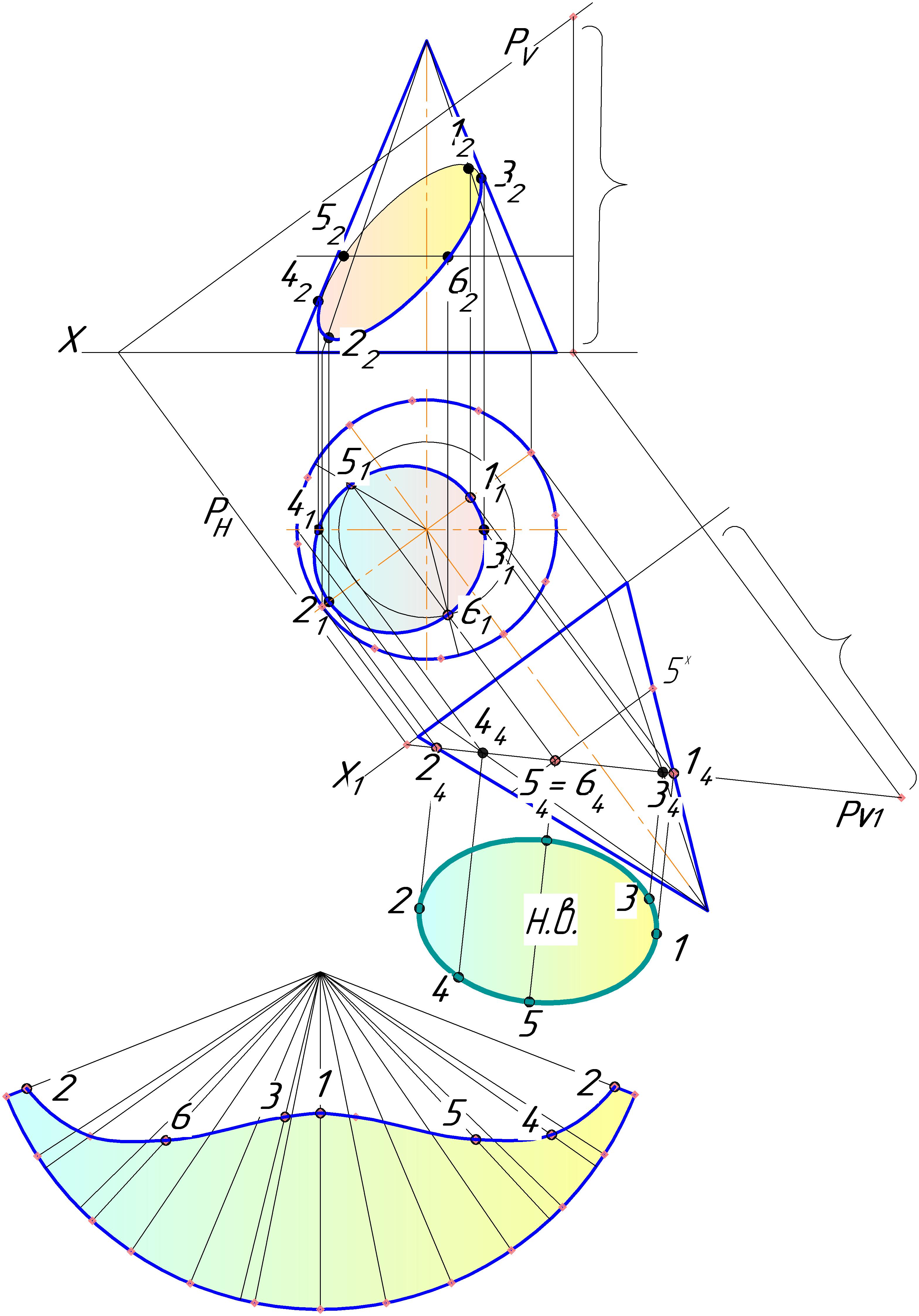
Рисунок 57 ‑ Сечение прямого кругового конуса плоскостью