Вказівки по виконанню типових завдань поточного та підсумкового контролю знань студентів з розділу «математична статистика»

1. Записати емпіричну функцію розподілу для вибірки, яка представлена статистичним рядом:

хі	-2	0	1	3
nі	8	12	10	4

Розв’язання: Емпіричною функцією розподілу називається функція, яка має вигляд ,

де n- обсяг вибірки, n_х- число значень випадкової величини Х у вибірці, які менші за х. Тоді запишемо емпіричну функцію розподілу

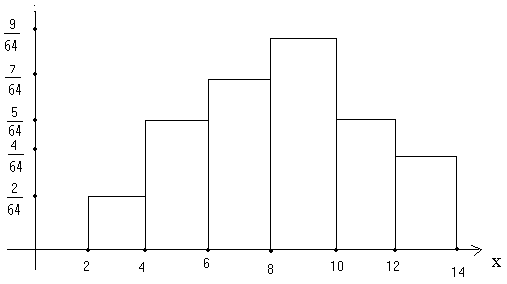
2. Побудувати гістограму частот для інтервального статистичного ряду

Х	2 - 4	4 - 6	6 - 8	8 - 10	10 - 12	12 - 14
nі	2	5	7	9	5	4

Розв’язання: Знайдемо суму частот вибірки: .

Нижче, на рисунку зображена гістограма. При цьому, основа кожного прямокутника дорівнює довжині інтервалу , а висота дорівнює .

3. Протягом 10 днів в банку фіксували кількість підписаних договорів за один день. Отримали наступну вибірку: 15, 20, 14, 17, 15, 22, 18, 17, 20, 21. Знайти вибіркове середнє, вибіркову дисперсію та незміщену вибіркову дисперсію для кількості підписаних договорів за один день.

Розв’язання: Для знаходження вибіркового середнього скористаємось формулою (2):

Вибіркову дисперсію знайдемо за формулою (4):

=

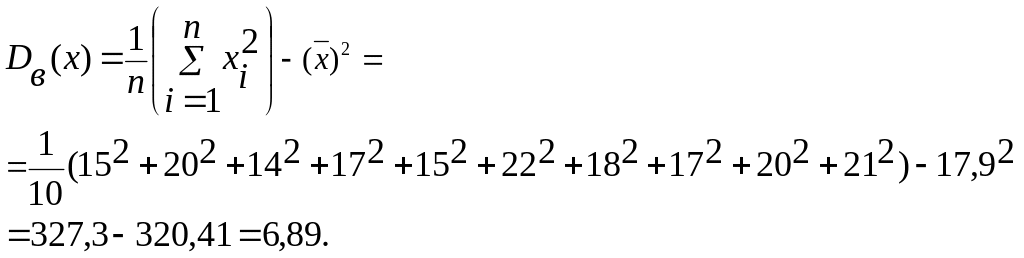Незміщена (виправлена) вибіркова дисперсія:

.

4. Із сукупності, що розподілена за нормальним законом зроблена вибірка об’єму . З надійністю знайти довірчий інтервал для математичного сподівання а, якщо дисперсія дорівнює а) , б) . Як зміниться довірчий інтервал, якщо об’єм вибірки збільшиться. Розв’язати задачу для випадку .

Розв’язання: За формулою (9) знайдемо t

. Тоді з таблиці 2 знайдемо число t=1,96.

З нерівності (8) отримаємо такий довірчий інтервал:

для випадку а):

для випадку б):

Отже, при збільшенні дисперсії довірчий інтервал збільшується, а отже точність оцінки зменшується.

У випадку отримаємо наступні довірчі інтервали:

а)

б)

5. Для даного інтервального статистичного ряду перевірити гіпотезу про нормальний закон розподілу при рівні значущості = 0.05.

Х	3,0-3,6	3,6-4,2	4,2-4,8	4,8-5,4	5,4-6,0	6,0-6,6	6,6-7,2
	2	8	35	43	22	15	5

Розв’язання: Перевіримо цю гіпотезу, скориставшись критерієм Пірсона. Нормальний закон розподілу залежить від двох параметрів: та . Замінимо ці параметри їх відповідними точковими оцінками . Для цього знайдемо вибіркове середнє та вибіркову дисперсію, причому за представника кожного інтервалу візьмемо його середину:

Отже .

Для нормального закону розподілу ймовірність попадання випадкової величини Х на інтервал знаходять за формулою:

,

де - функція Лапласа (див. Таблицю 2). Знайдемо значення теоретичних частот для кожного інтервалу. Покажемо як це робиться на прикладі третього інтервалу:

Потім складаємо порівняльну таблицю чисел: статистичних частот і відповідних їм значень ( ).

інтервали	3,0-3,6	3,6-4,2	4,2-4,8	4,8-5,4	5,4-6,0	6,0-6,6	6,6-7,2
	2	8	35	43	22	15	5
	2,48	11,23	28,46	39,60	30,92	13,45	3,25

За формулою (13) визначаємо міру відхилення емпіричних частот від теоретичних: .

Визначимо за формулою (14) число степенів свободи: k=7-2-1=4. За таблицею 3 знайдемо критичне значення критерію при рівні значущості : .

Відповідь: оскільки спостережене значення критерію менше ніж критичне, то гіпотеза про нормальний закон розподілу приймається.

6. В таблиці представлені статистичні дані про капітальні вкладення Х (в тис. грн..) і чистий дохід У (в тис. грн..). Знайти рівняння лінії регресії.

Х=хі	1	2	3	4	5	6	7
У=уі	3,0	3,5	4,0	4,2	4,6	5,0	5,2

Розв’язання: Спочатку знайдемо числові характеристики (вибіркове середнє, дисперсію, середнє квадратичне відхилення) окремо для випадкової величини Х та У.

,

,

,

.

Тоді відповідні середньоквадратичні відхилення будуть

, .

Оскільки так як дані таблиці не повторюються, то для обчислення кореляційного моменту скористаємось формулою (15). В даному випадку будемо мати: . Тоді вибірковий коефіцієнт кореляції знайдемо за формулою (17):

.

Підставимо знайдені значення в рівняння (18) і отримаємо:

.

Отже, рівняння лінії регресії має вигляд .

КИЇВСЬКИЙ НАЦІОНАЛЬНИЙ ЕКОНОМІЧНИЙ УНІВЕРСИТЕТ (денна форма)

Кафедра вищої математики

Навчальний предмет теорія ймовірностей та математична статистика

Спеціальність Семестр 2