31. Закон больших чисел

Закон больших чисел(с док-вом) Пусть S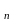 - число успехов в серии из n независимых испытаний в схеме Бернулли с вероятностью успеха p, 0<p<1. Тогда при любом t>0 справедливо равенство Доказательство Как отмечалось ранее, MS = np, DS =npq. Имеем . Применим неравенство Чебышева, положив в нем Х=S и 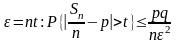что и т.д. Закон больших чисел утверждает,что при больших n и при сколь угодно малых ε разность между частотой успеха S_n /n и вероятностью успеха в каждом испытании p по модулю меньше ε с вероятностью, близкой к 1.

Пример В большом городе в год рождается 20000 детей. Считая вероятность рождения мальчика p=0,5 найти такое число t, чтобы с вероятностью 0,99 можно было утверждать,что число рожденных мальчиков превышает число девочек не более чем на t.

Решение. Решаем задачу по схеме Бернулли с n=20000,p=0,5.Пусть S -число рождений мальчиков, тогда (n- S )-число рождений девочек; разность между ними равна(2 S_n - n).Найдем такое t, чтобы P{|2 S -n |>t}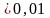 . Воспользуемся неравенством Чебышева: . Выбираем t из условия

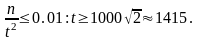
32. Функция распределения случайной величины

Ф-я распред-я случ. величины X – ф-я F(x), выражающая для каждого х

в ер-сть того, что случ. величина X примет значение, меньшее х. F(x) также называют интегральной ф-ей распределения. Пример: Ф-я распределения есть разрывная ступенчатая ф-я, скачки которой происходят в точках, соответствующих возможным значениям случ. величины и равны вер-стям этих значений. Сумма всех скачков F(x) = 1. Свойства F(x):

1) 0≤F(x)≤1 – следует из того, что F(x) - это вероятность.

2) F(x) - неубывающая ф-я на всей числовой оси.

3) F(-∞)=lim F(x)=0 (x→ - ∞) – вер-сть невозможного соб-я, F(+∞)=lim F(x)=1 (x→ +∞) – вер-сть достоверного соб.

4)Вер-сть попадания Х в интервал: P(x1≤X≤x2)=F(x2)-F(x1).

33. Непрерывные случайные величины. Плотность вероятности

Непрерывной называют величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины бесконечно.

Плотность вероятности.

Плотностью распределения вероятностей непрерывной случайной величины X называется функция - первую производную от функции распределения

.

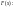
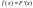Функция распределения является первообразной для плотности распределения.

Свойства плотности распределения.

Свойство 1: Плотность распределения – неотрицательная функция .

Доказательство: Функция распределения – неубывающая функция, следовательно, её производная 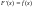- функция неотрицательная. Геометрически это означает, что точки, принадлежащие графику плотности распределения, расположены либо над осью Ox, либо на этой оси. График плотности распределения называют кривой распределения.

Свойство 2: Несобственный интеграл от плотности распределения в переделах от 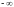до равен 1.

Доказательство: Несобственный интеграл выражает вероятность события, состоящего в том, что случайная величина примет значение, принадлежащее интервалу ( , ). Очевидно, такое событие достоверно, следовательно, вероятность его равна 1.

Теорема: Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (a,b), равна определенному интегралу от плотности распределения, взятому в пределах от a до b:

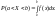
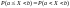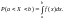Доказательство: Используем соотношение то, что Таким образом, Так как , то окончательно получим => Вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (a,b), равна площади криволинейной трапеции, ограниченной осью Ox, кривой распределения и прямыми x=a и x=b.