- •1)События и их виды
- •2)Классическое определение вероятности .Примеры
- •3)Относительная частота. Теорема бернулли
- •4) Теоремы сложения вероятностей
- •5)Теоремы умножения вероятностейпроизведение событий. Теорема умножения
- •6) Многократные испытания. Формула бернулли. Вероятнейшее число появлений события
- •7) Формы задания закона распределения дискретных случайных величин
- •2.1 Виды случайных величин
- •2.2 Формы задания закона распределения дискретных случайных величин
- •8) Формы задания закона распределения для непрерывных случайных величин формы задания закона распределения для непрерывных случайных величин
- •9) Вероятность попадания случайной величины на заданный интервал
- •10) Математическое ожидание и его свойства
- •11)Моменты.
- •12)Дисперсия.
- •13)Нормальный закон распределения
- •3.1 Нормальный закон и его основные параметры
- •14) Понятие о центральной предельной теореме
- •15) Вероятность попадания нормально распределённой случайной величины на заданный интервал вероятность попадания нормально распределённой случайной величины на заданный интервал
- •16)Интеграл вероятностей
- •17)Вероятное отклонение и его связь со средним квадратическим отклонением при нормальном законе распределения
- •18Среднее отклонение и его связь со средним квадратическим отклонением при нормальном законе распределения
- •19)Основные понятия математической статистики
- •21) Понятие о наилучших оценках
- •22) Понятие о доверительных интервалах доверительные интервалы и доверительная вероятность
- •23)Коэффициент корреляции и его свойства
- •5.1 Понятие о статистических связях
- •5.2 Коэффициент корреляции
- •24) Уравнение регрессии.Его достоинства уравнение регрессии
- •3. Составим уравнение регрессии на d:
- •25) Основные задачи теории ошибок
- •26)Классификация ошибок измерений
- •27) Критерии точности измерений критерии точности измерений
- •28)Свойства случайных ошибок измерений
- •29) Исследование ряда истинных ошибок на нормальное распределение
- •30) Средняя квадратическая ошибка функции
- •32) Общие сведения о весах
- •Обратный вес функции общего вида
- •33)Вывод формулы среднего арифметического - доброкачественной оценки неизвестного истинного значения
- •34) Уклонения ср-его арифм-ого и их св-ва
- •37) Вывод формулы Среднего Весового
- •Двойные неравноточные измерения
11)Моменты.
В теории вероятностей для характеристики основных свойств распределения часто применяют моменты.
Начальным моментом k‑го порядка случайной величины Х называют математическое ожидание k‑й степени этой случайной величины
|
|
Для дискретной случайной величины начальные моменты k-го порядка вычисляют по формуле
|
|
для непрерывной величины — по формуле
|
|
При
имеем
![]() ,
т.е. приходим к основной характеристике
положения: математическому ожиданию
случайной величины Х.
,
т.е. приходим к основной характеристике
положения: математическому ожиданию
случайной величины Х.
Центральным
моментом порядка k
случайной величины Х называют
математическое ожидание k‑й степени
соответствующей центрированной случайной
величины ![]()
|
|
Центральные моменты дискретной случайной величины вычисляют по формуле
|
|
для непрерывной величины — по формуле
|
|
Особое значение
имеет центральный момент второго
порядка, называемый дисперсией.
Применяют обозначения:
![]() и
и
![]() .
.
|
|
12)Дисперсия.
Дисперсия характеризует степень разброса значений случайной величины относительно математического ожидания (центра распределения).
Особое значение имеет центральный момент второго порядка, называемый дисперсией. Применяют обозначения: и .
, |
|
Свойства дисперсии:
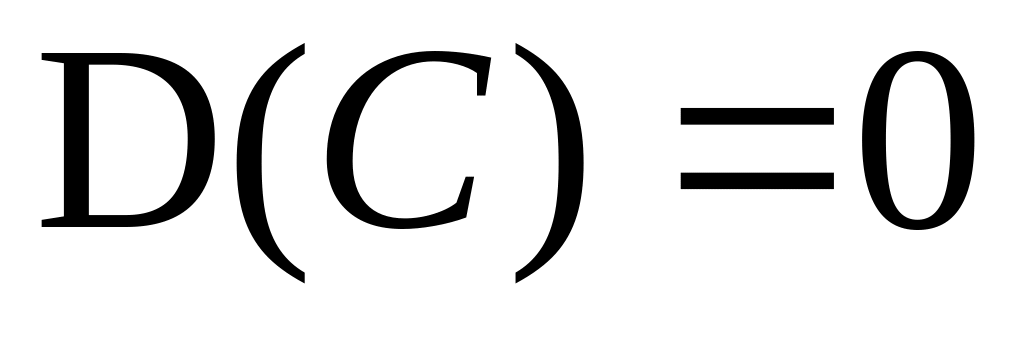 ;
;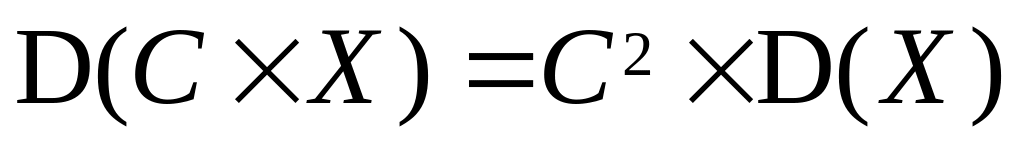 ;
;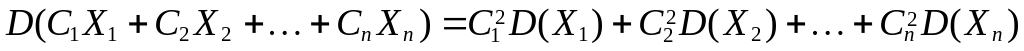 ,
если
—
независимые случайные величины.
,
если
—
независимые случайные величины.
Дисперсия имеет размерность квадрата случайной величины. Для наглядной характеристики рассеивания удобнее пользоваться средним квадратическим отклонением (СКО, положительной величиной корня квадратного из дисперсии):
|
|
Задача 2.4. Случайная величина Х задана рядом распределения:
x |
0 |
1 |
2 |
3 |
p |
0,34 |
0,44 |
0,19 |
0,03 |
Найти
её основные параметры:
,
,
![]() .
.
Решение: применяя формулы , и , имеем
![]() ;
;
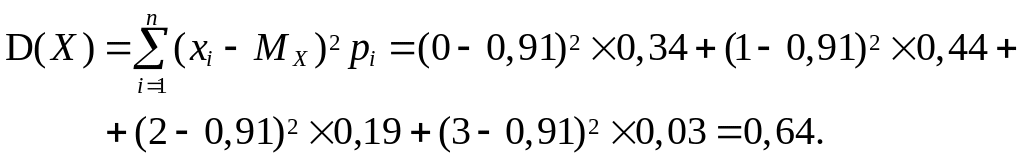
Дисперсию можно найти и по формуле связи центральных и начальных моментов:
|
|
![]() ;
;
![]() ;
;
![]() .
.
Находим
СКО:
![]() .
.
Задача 2.5. Найти основные параметры непрерывной случайной величины Х, закон распределения которой задан в условии задачи 2.3.
Решение: находим
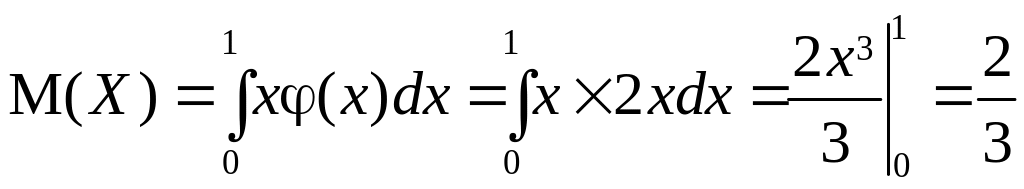 .
.
![]() ;
;
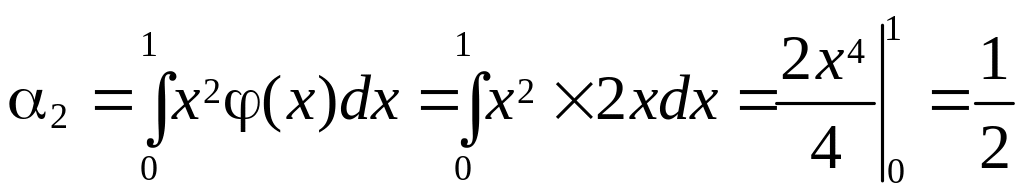 .
.
![]() ;
;
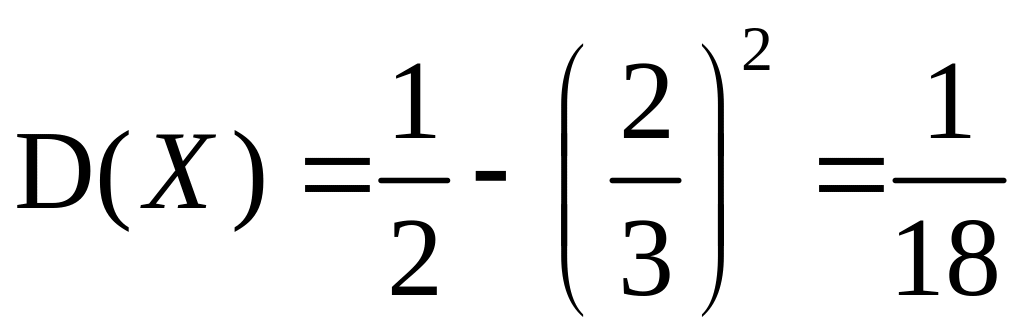 ,
тогда
,
тогда
![]() .
.
13)Нормальный закон распределения
Случайная величина X с плотностью распределения вида
|
|
и графиком плотности, представленным на рис. 3.1, считается распределённой по нормальному закону.
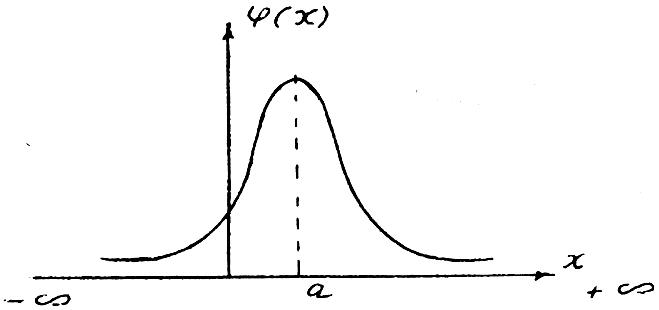
Рис. 3.1 — Кривая плотности нормального закона
3.1 Нормальный закон и его основные параметры
Кривая распределения по нормальному закону имеет симметричный колоколообразный вид.
Применяя формулы ,
и , можно
показать, что величины а и 2,
входящие в выражение ,
являются основными параметрами нормально
распределённой случайной величины X:
![]() ,
,
![]() .
.
При изменении
параметра a кривая
,
не изменяя своей формы, перемещается
вдоль оси абсцисс. При изменении
параметра ![]() форма кривой изменяется (если
форма кривой изменяется (если
![]() ,
то параметру
,
то параметру ![]() соответствует более узкая в направлении
оси ординат кривая, то есть меньший
разброс значений xi
относительно параметра
,
и более высокое положение вершины
кривой).
соответствует более узкая в направлении
оси ординат кривая, то есть меньший
разброс значений xi
относительно параметра
,
и более высокое положение вершины
кривой).

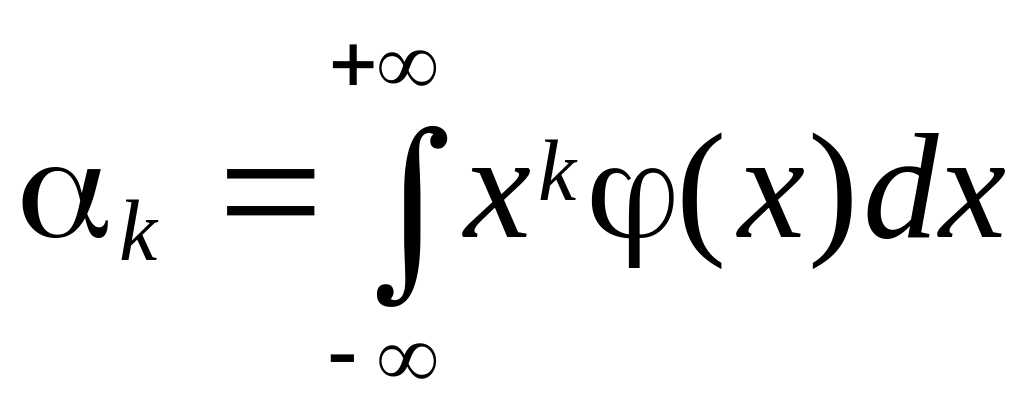 .
.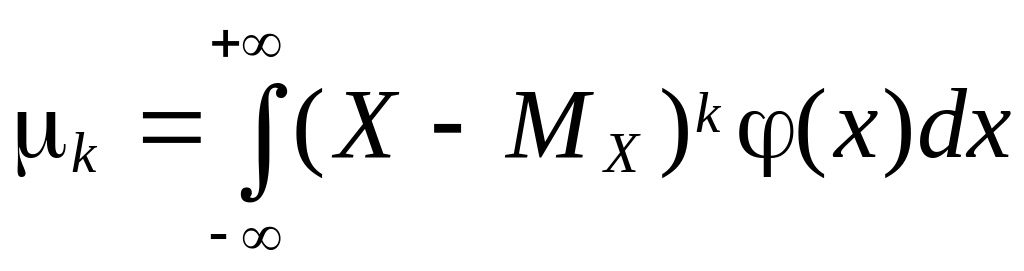 ,
,