Обратный вес функции общего вида

Пусть дана функция   , где  — независимо измеренные величины. Известны их веса .

Используя формулы  и , получаем следующую формулу для вычисления обратного веса функции:

.

Если величины коррелированы, т.е. коэффициенты попарной корреляционной связи отличны от нуля, , то обратный вес функции вычисляется по формуле:

.

Задача 4.2. Найти веса следующих функций

1. ;

2.  

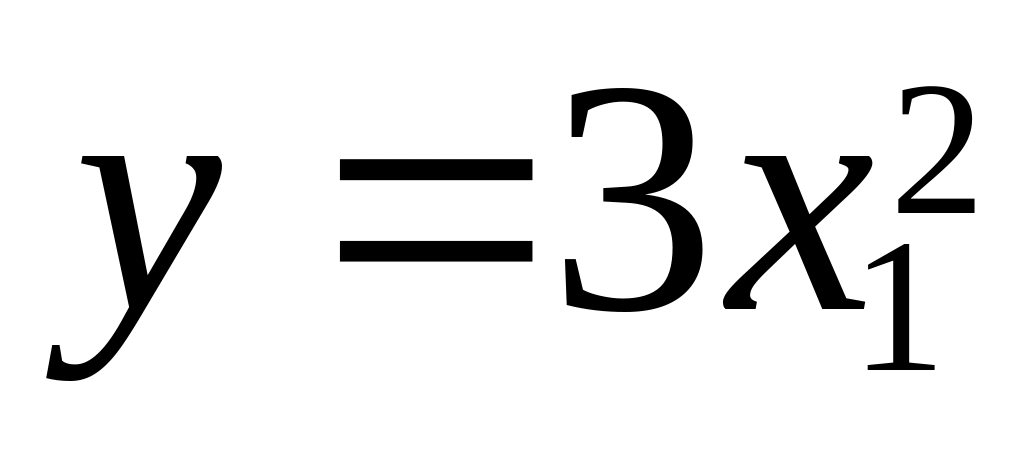
если ; ; ; , .

Решение:

1. ; ;

2. ; .

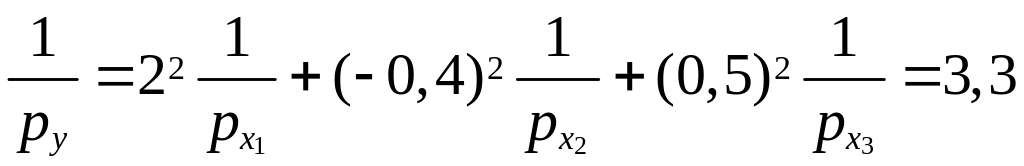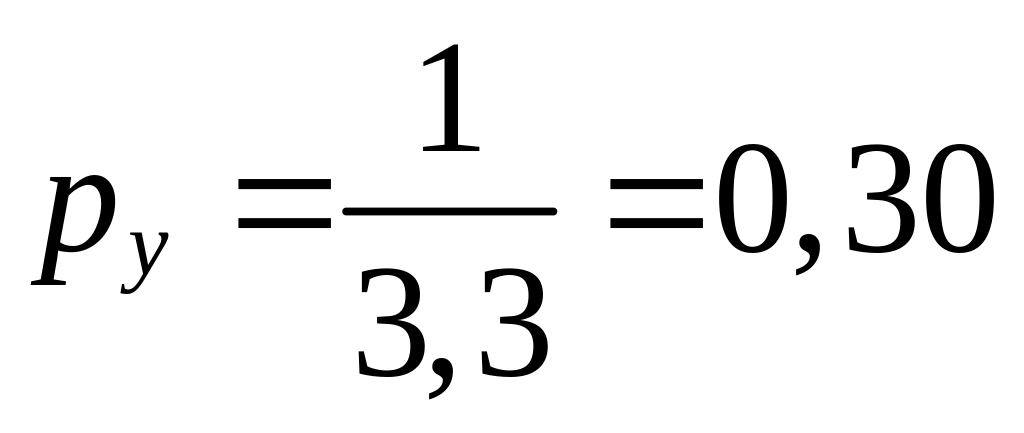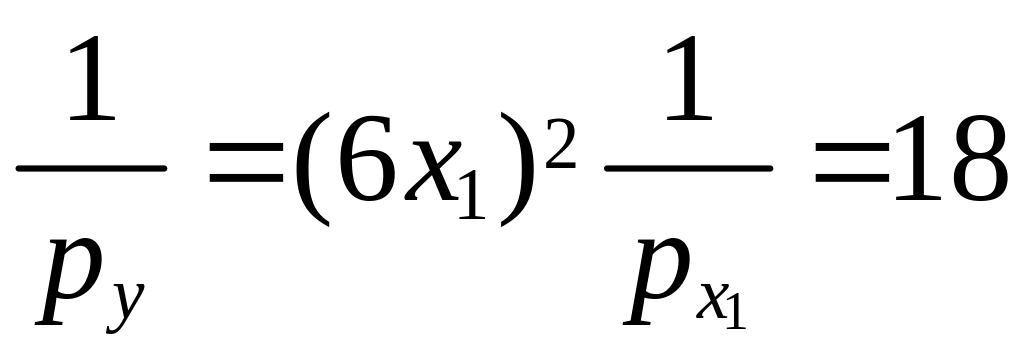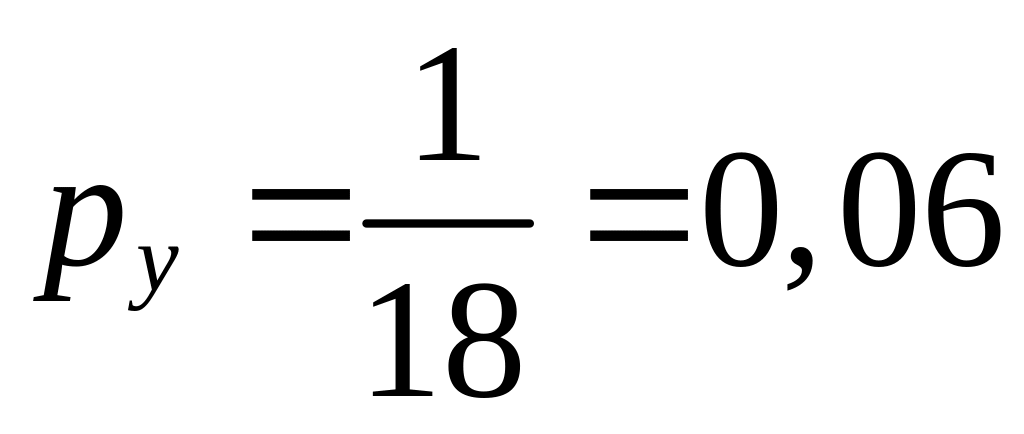33)Вывод формулы среднего арифметического - доброкачественной оценки неизвестного истинного значения

34) Уклонения ср-его арифм-ого и их св-ва

36) Ср-яя кв-ая ош-ка срелнего арифм-ого (наиб.надежного значения)

3. Определение средней квадратической ошибки наиболее надёжного значения измеряемой величины:

.

37) Вывод формулы Среднего Весового

Пусть имеется ряд многократных неравноточных измерений одной и той же величины: , истинное значение Х которой неизвестно. Известны веса результатов измерений: .

Под математической обработкой ряда неравноточных измерений понимают:

1. Определение наиболее надёжного значения измеряемой величины — среднего весового, или общей арифметической средины (наилучшей оценки неизвестного истинного значения):

,

где x₀ — наименьшее значение из ряда , а .

38) Свойства уклонений от среднего весового

2. Определение по формуле Бесселя средней квадратической ошибки измерения с весом, равным единице (оценки параметра  ):

,

где  — уклонения от среднего весового, которые обладают свойствами:

1. ,

2. 

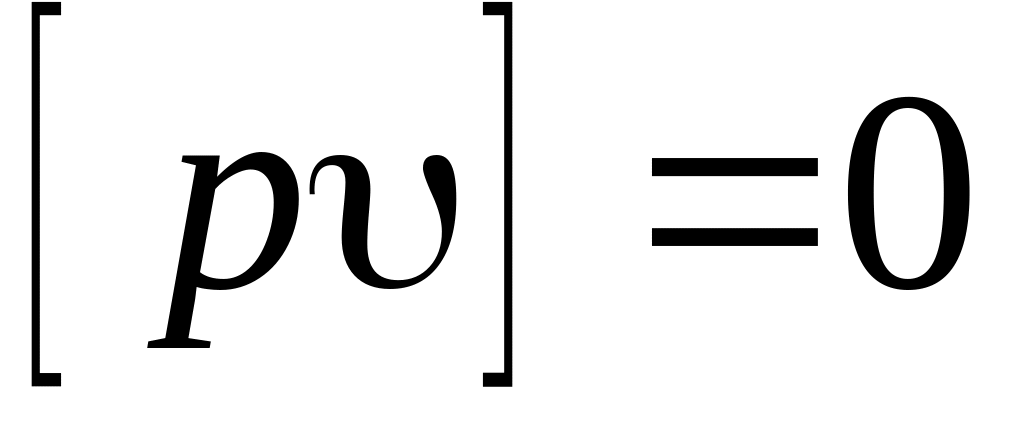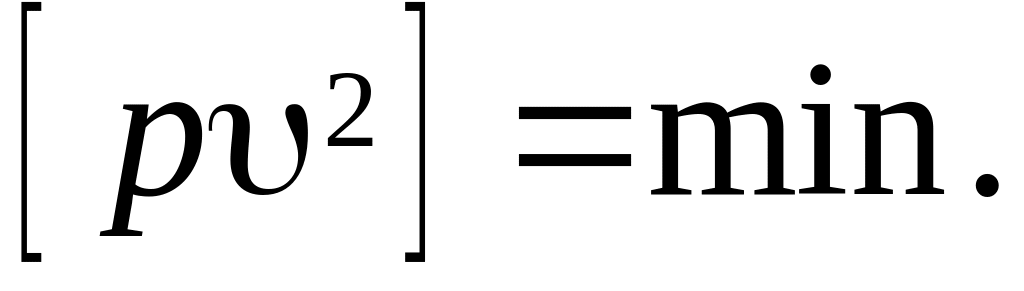
39)Вывод формулы Бесселя по ряду неравноточных измерений одной величины

Определение по формуле Бесселя средней квадратической ошибки измерения с весом, равным единице (оценки параметра  ):

,

где  — уклонения от среднего весового

40) Ср-яя кв-ая ош-ка среднего весового

41) Доверительный интервал для мат. Ожидания

42) Доверительный интервал для ср.кв.отклонения отдельного результата

43) Оценка точности по разностям двойных измерений. Критерий обнаружения систематических ошибок.

ДВОЙНЫЕ РАВНОТОЧНЫЕ ИЗМЕРЕНИЯ

Пусть однородные величины измерены равноточно дважды и получены результаты измерений:

Составим разности по формуле

.

Наиболее надёжные значения определяемых величин находим по формуле:

.

Для оценки точности используем разности .

1. При отсутствии систематических ошибок разности d_i можно рассматривать как истинные ошибки самих разностей, так как истинное значение разностей равно нулю ( ).

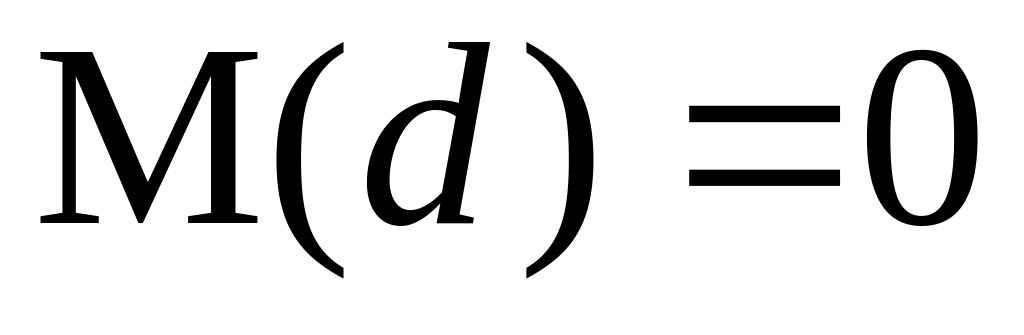Применяя к ряду  формулу Гаусса , находим:

.

Тогда средняя квадратическая ошибка отдельного результата измерений будет определяться по формуле:

.

Оценка точности наиболее надёжных значений определяется по формуле:

.

2. Если в результатах измерений присутствуют систематические ошибки, то величина

существенно отличается от нуля.

В этом случае из каждой разности необходимо исключить остаточное влияние систематических ошибок, т. е. получить разности

.

Рассматривая разности  как уклонения от среднего  , применяя формулу Бесселя, находим

.

Средние квадратические ошибки отдельного результата измерений и наиболее надёжных значений измеряемых величин находим по формулам:

,
.

Заметим, что в этом случае необходимо выполнить контроль вычислений по формулам

, где ; .

Для определения значимости отклонения от нуля применяют неравенство

,

где выбирают из таблиц Стьюдента по заданной вероятности и числу степеней свободы  , а при  коэффициент t выбирают из таблиц интеграла вероятностей по заданной вероятности  . Так, для  , и неравенство  принимает вид:

.

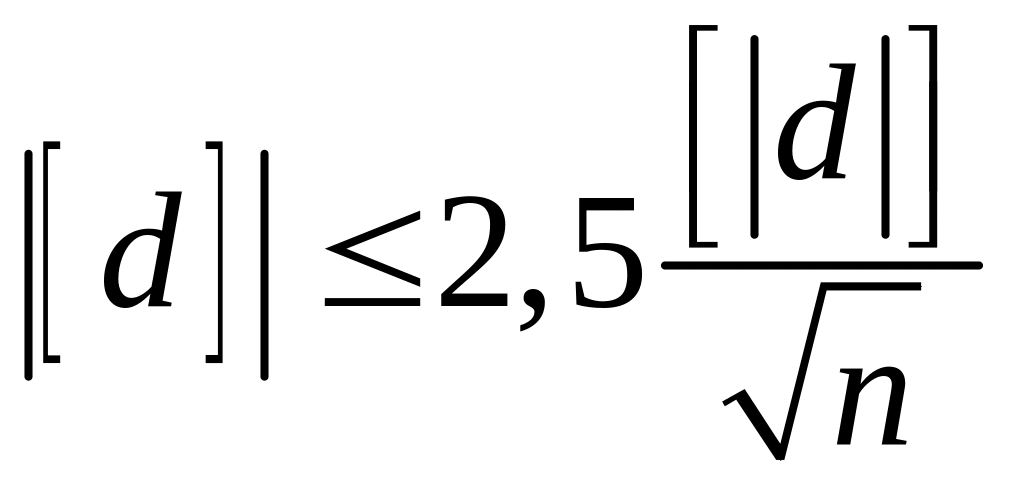Иногда применяют более жёсткий критерий обнаружения систематических ошибок

,

который получен, исходя из требования .

Оценку точности начинают с проверки условия  или . Если, например, неравенство  выполняется, то делают вывод о том, что систематическими ошибками можно пренебречь и оценку точности следует выполнять по формулам (5.4–5.5).

Если неравенство  не выполняется, делают заключение о том, что систематическими ошибками пренебрегать нельзя, необходимо обработку вести по формулам (5.7, 5.9, 5.10).
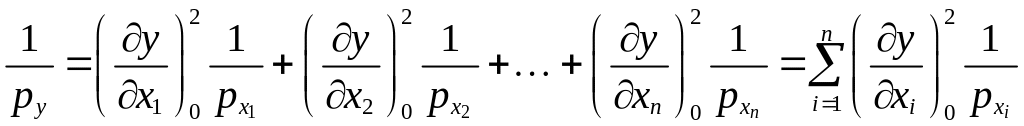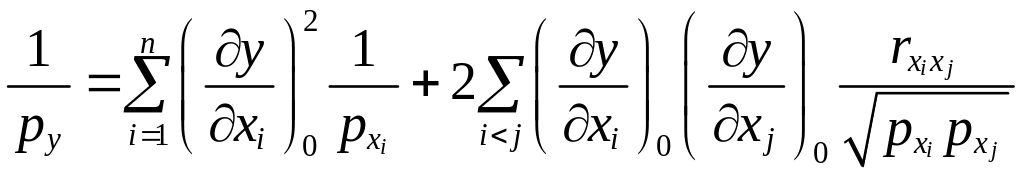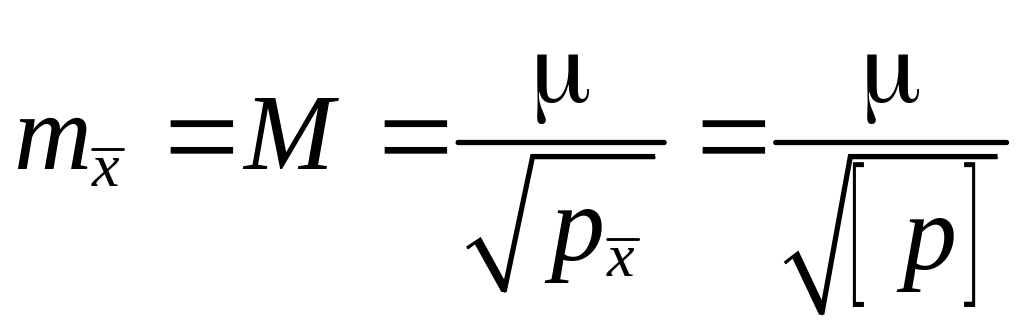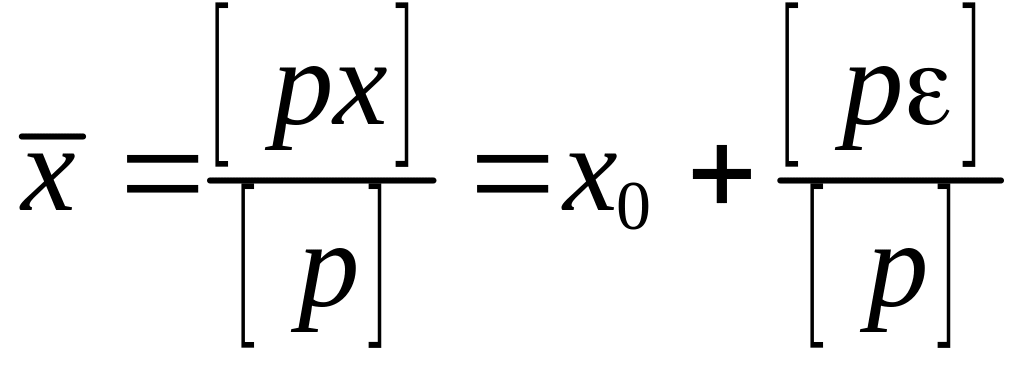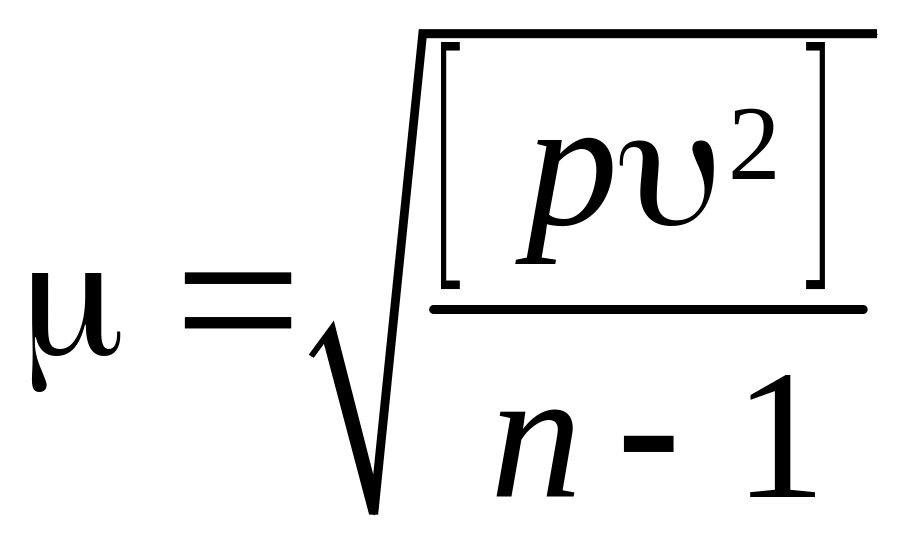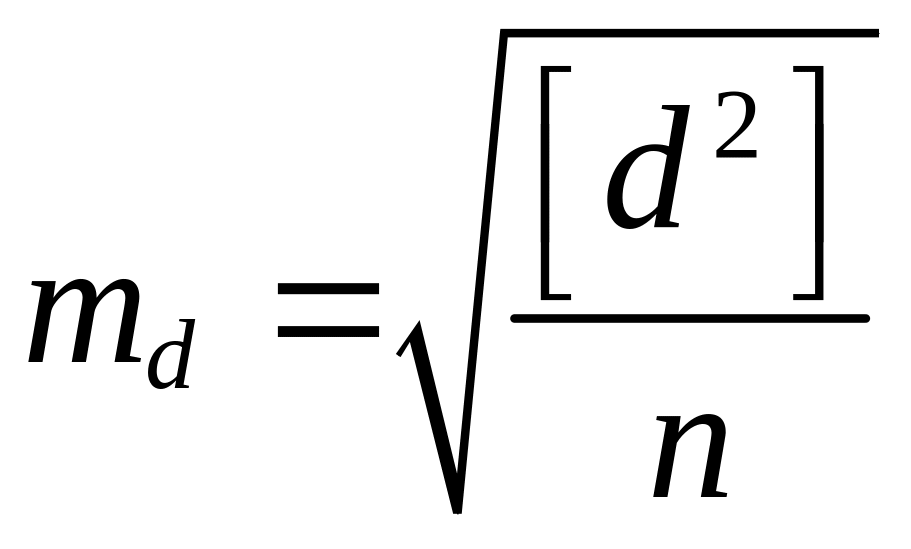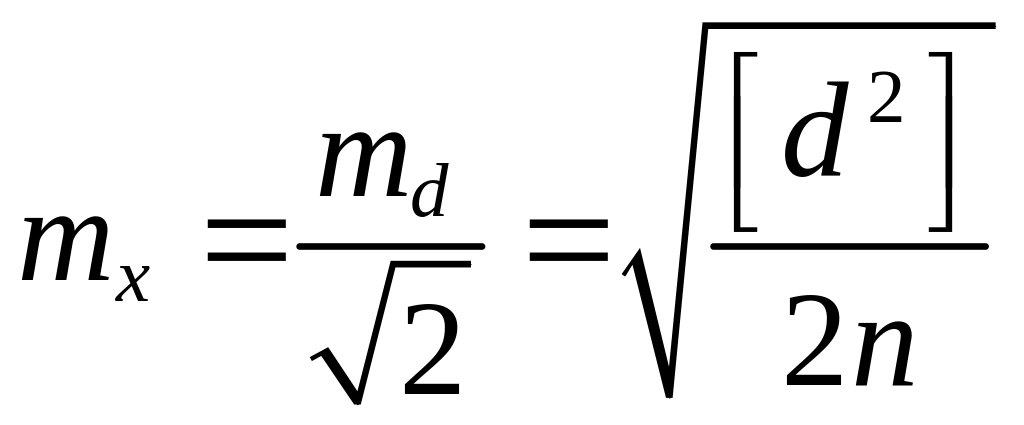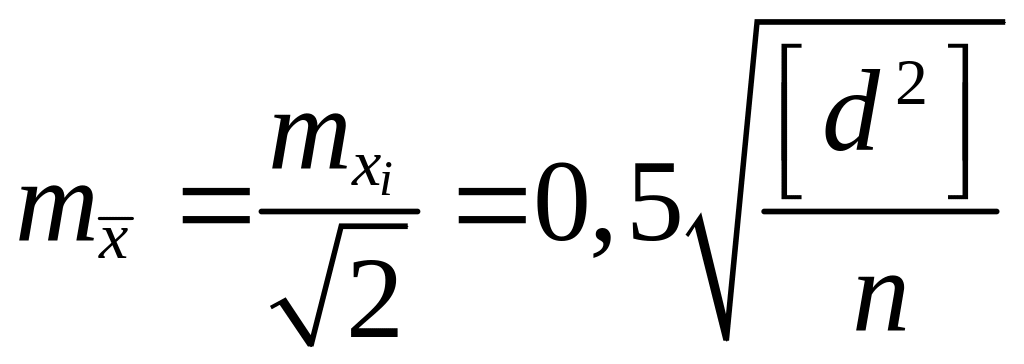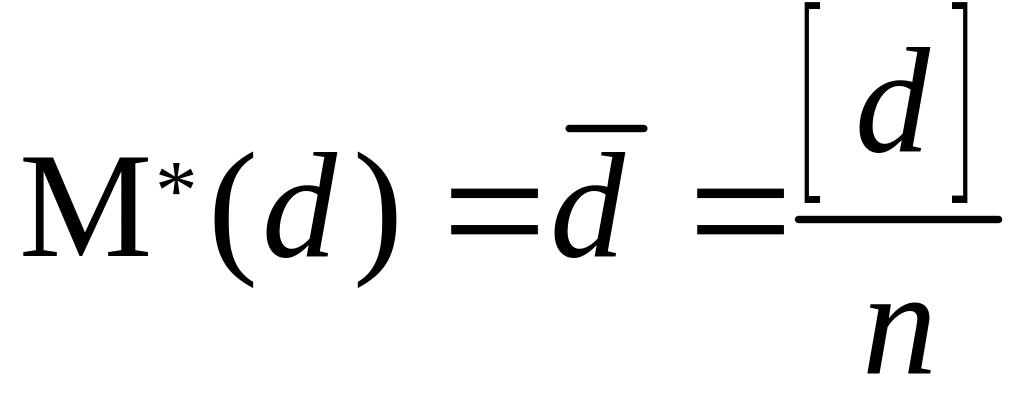
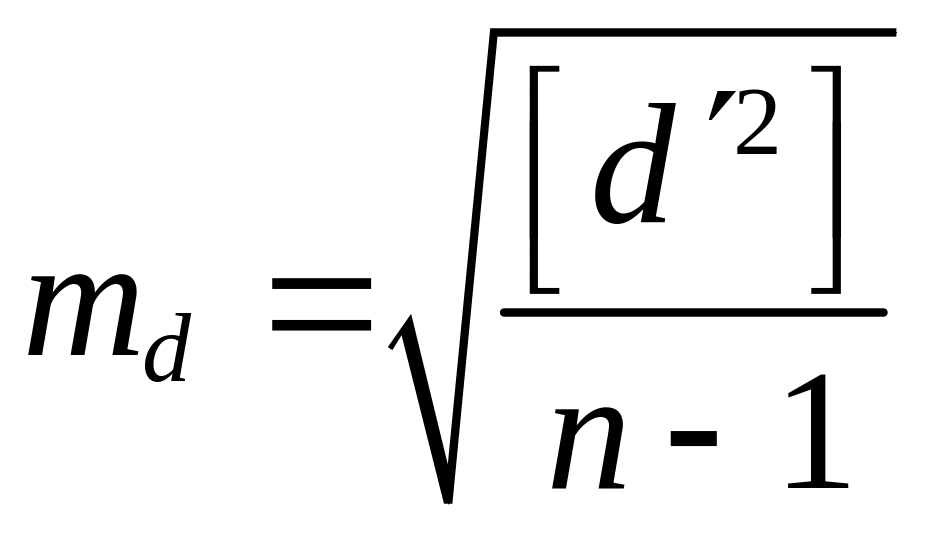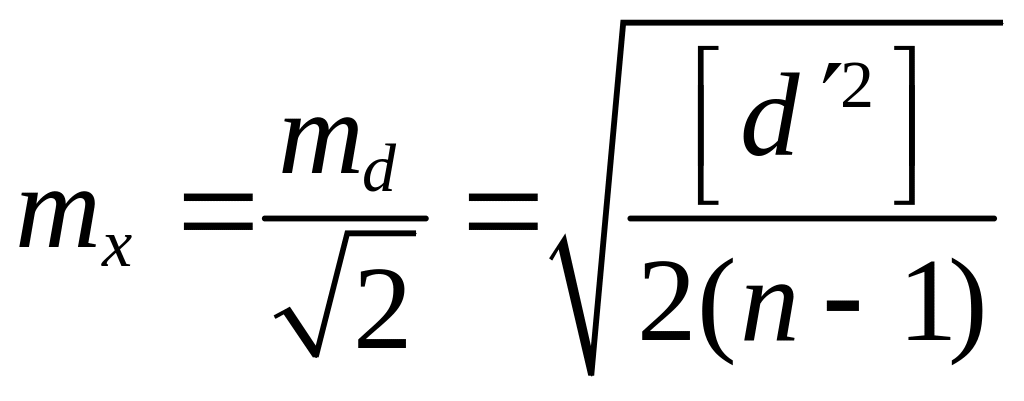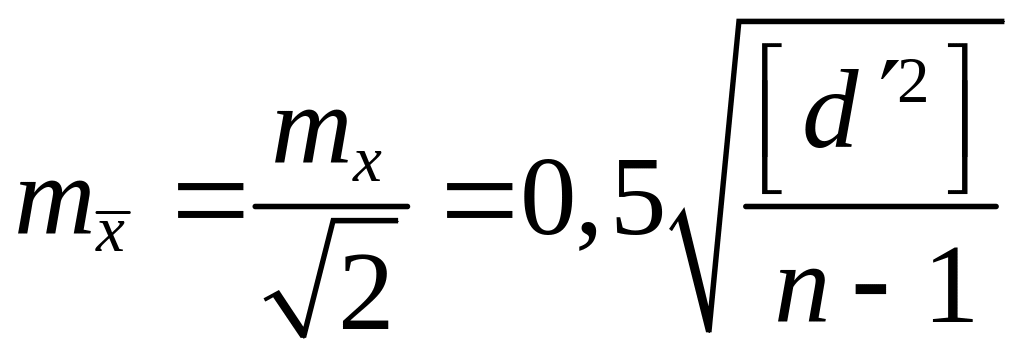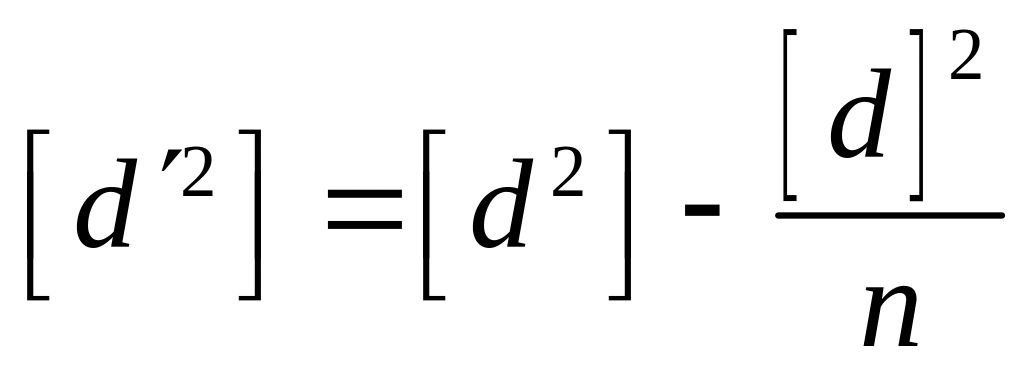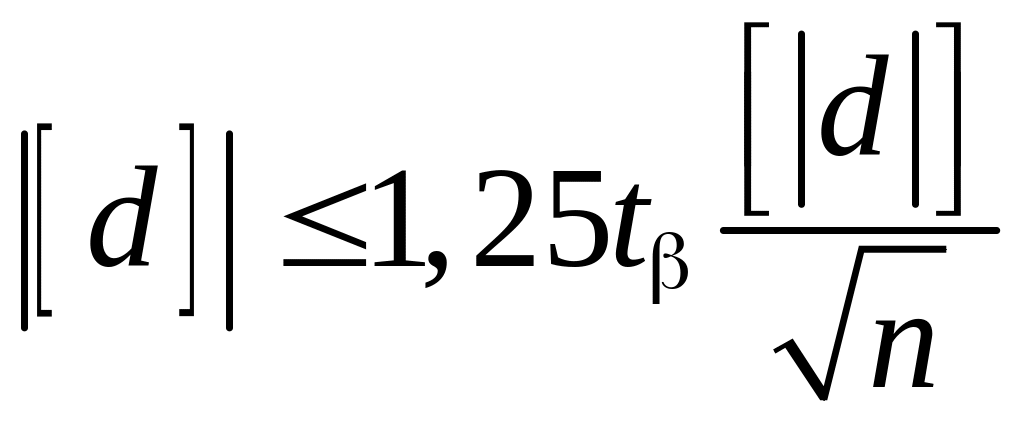