1. Двойные неравноточные измерения

Пусть каждая из однородных величин Х_i ( ) измерена дважды и независимо, причём измерения в каждой паре равноточны, а пары между собой неравноточны. Известны веса р_i результатов измерений. Получены разности d_i с весами .

Наиболее надёжные значения измеряемых величин находит по формуле .

Критерий обнаружения систематических ошибок имеет вид:

.

Если неравенство выполняется, то делают заключение о том, что систематическими ошибками можно пренебречь. Затем находят:

1. Среднюю квадратическую ошибку измерения с весом, равным единице,

   .

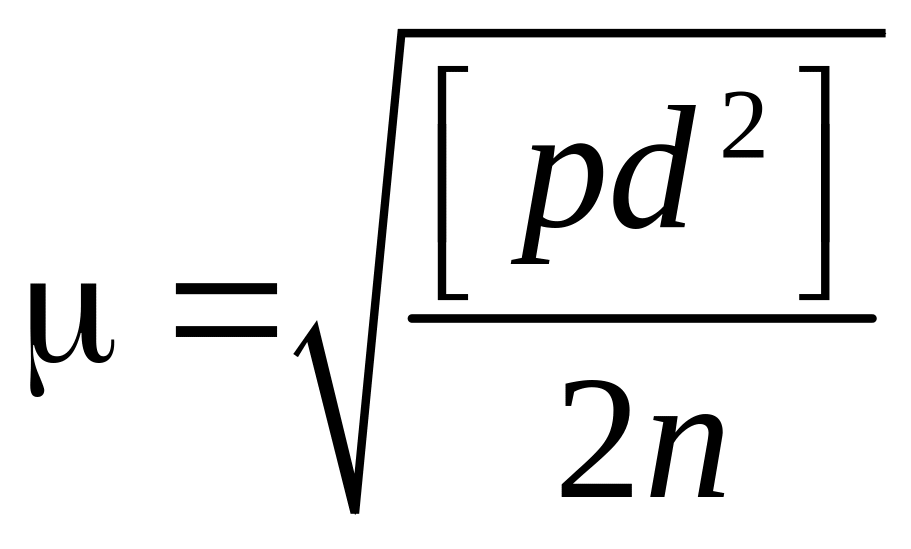2. Средние квадратические ошибки наиболее надёжных значений

.

Если условие  не выполняется, то необходимо найти остаточное влияние систематических ошибок

и исключить его из каждой разности. Получают разности, свободные от влияния систематических ошибок

.

Оценка точности выполняется следующим образом:

1. Определяется средняя квадратическая ошибка измерения с весом, равным единице

   .

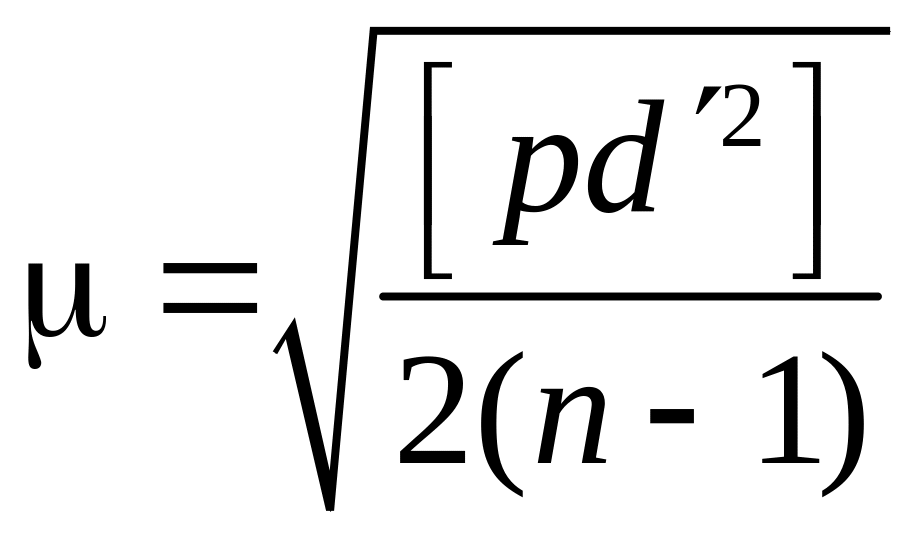2. Вычисляются средние квадратические ошибки наиболее надёжных значений

.

1 Так при из таблиц Приложения B получаем , т.е. с вероятностью, близкой к единице, можно утверждать, что случайные ошибки не превзойдут предела, равного "3m".

⁾ Критерий обнаружения постоянной систематической ошибки имеет вид [1, стр.95]

,

где t выбирается из таблиц Приложения B (при ) по вероятности .

Находим для : и .

Как видно из результатов вычислений, критерий выполняется, так как

,

следовательно, с вероятностью 0,95 постоянной систематической ошибкой можно пренебречь и считать, что .

⁾ Для того чтобы оба слагаемых в этом выражении имели одинаковую размерность (в м²), необходимо во втором слагаемом величину  разделить на ² (т.е. выразить в радианной мере).
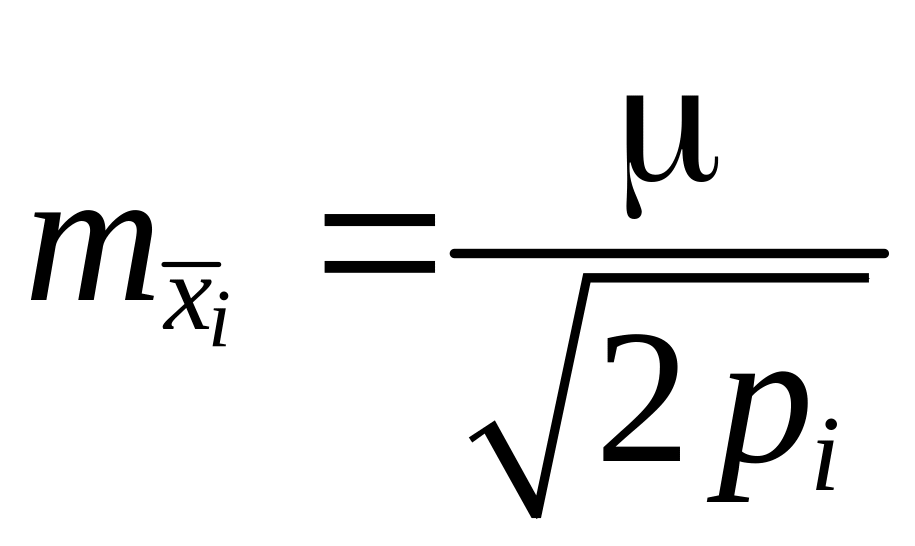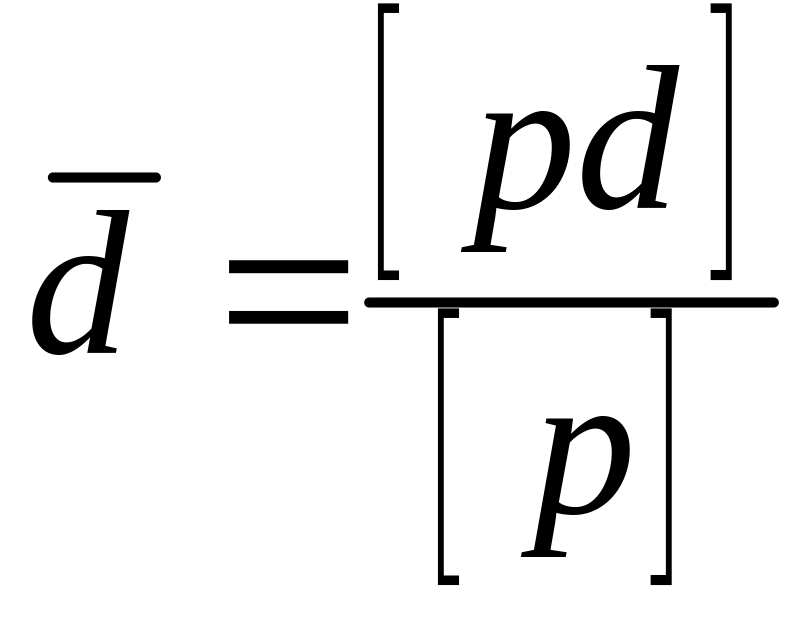
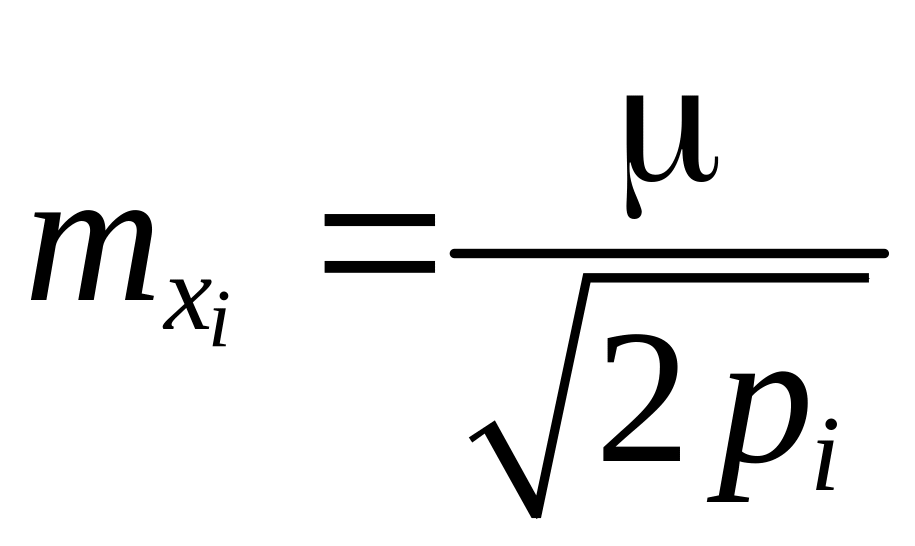