
- •1)События и их виды
- •2)Классическое определение вероятности .Примеры
- •3)Относительная частота. Теорема бернулли
- •4) Теоремы сложения вероятностей
- •5)Теоремы умножения вероятностейпроизведение событий. Теорема умножения
- •6) Многократные испытания. Формула бернулли. Вероятнейшее число появлений события
- •7) Формы задания закона распределения дискретных случайных величин
- •2.1 Виды случайных величин
- •2.2 Формы задания закона распределения дискретных случайных величин
- •8) Формы задания закона распределения для непрерывных случайных величин формы задания закона распределения для непрерывных случайных величин
- •9) Вероятность попадания случайной величины на заданный интервал
- •10) Математическое ожидание и его свойства
- •11)Моменты.
- •12)Дисперсия.
- •13)Нормальный закон распределения
- •3.1 Нормальный закон и его основные параметры
- •14) Понятие о центральной предельной теореме
- •15) Вероятность попадания нормально распределённой случайной величины на заданный интервал вероятность попадания нормально распределённой случайной величины на заданный интервал
- •16)Интеграл вероятностей
- •17)Вероятное отклонение и его связь со средним квадратическим отклонением при нормальном законе распределения
- •18Среднее отклонение и его связь со средним квадратическим отклонением при нормальном законе распределения
- •19)Основные понятия математической статистики
- •21) Понятие о наилучших оценках
- •22) Понятие о доверительных интервалах доверительные интервалы и доверительная вероятность
- •23)Коэффициент корреляции и его свойства
- •5.1 Понятие о статистических связях
- •5.2 Коэффициент корреляции
- •24) Уравнение регрессии.Его достоинства уравнение регрессии
- •3. Составим уравнение регрессии на d:
- •25) Основные задачи теории ошибок
- •26)Классификация ошибок измерений
- •27) Критерии точности измерений критерии точности измерений
- •28)Свойства случайных ошибок измерений
- •29) Исследование ряда истинных ошибок на нормальное распределение
- •30) Средняя квадратическая ошибка функции
- •32) Общие сведения о весах
- •Обратный вес функции общего вида
- •33)Вывод формулы среднего арифметического - доброкачественной оценки неизвестного истинного значения
- •34) Уклонения ср-его арифм-ого и их св-ва
- •37) Вывод формулы Среднего Весового
- •Двойные неравноточные измерения
8) Формы задания закона распределения для непрерывных случайных величин формы задания закона распределения для непрерывных случайных величин
Функция распределения.
Для непрерывной случайной величины график функции распределения (рис. 2.3) имеет форму плавной кривой.
Свойства функции распределения:
;
;
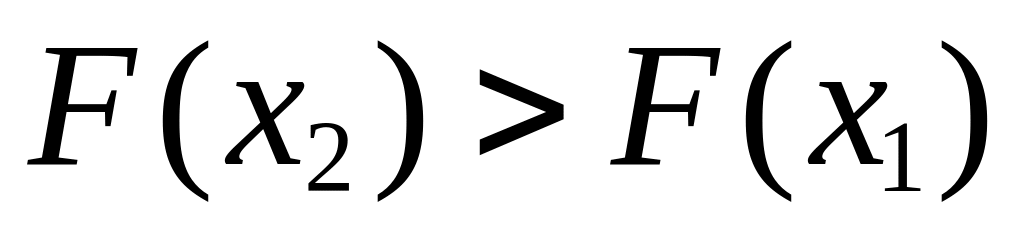 ,
если
.
,
если
.
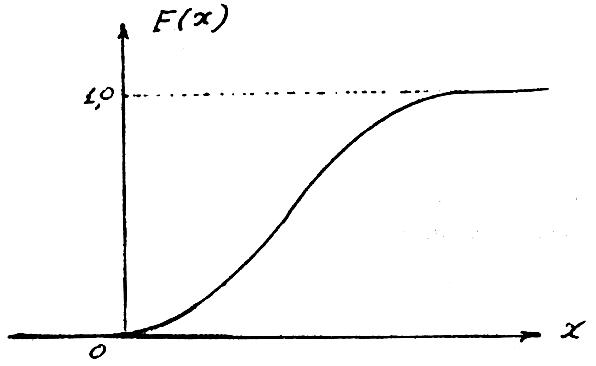
Рис. 2.3 — Функция распределения непрерывной величины
Плотность распределения определяется как производная от функции распределения, т.е.
|
|
Кривая, изображающая плотность распределения случайной величины, называется кривой распределения (рис. 2.4).
Свойства плотности:
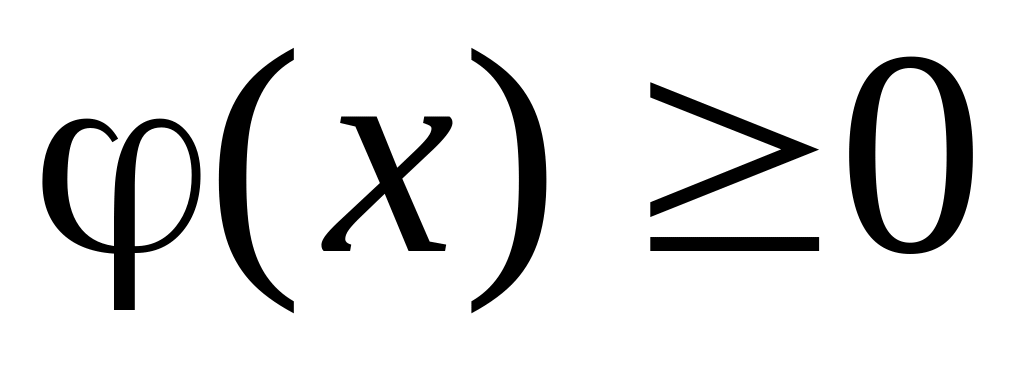 ,
т.е. плотность есть неотрицательная
функция;
,
т.е. плотность есть неотрицательная
функция;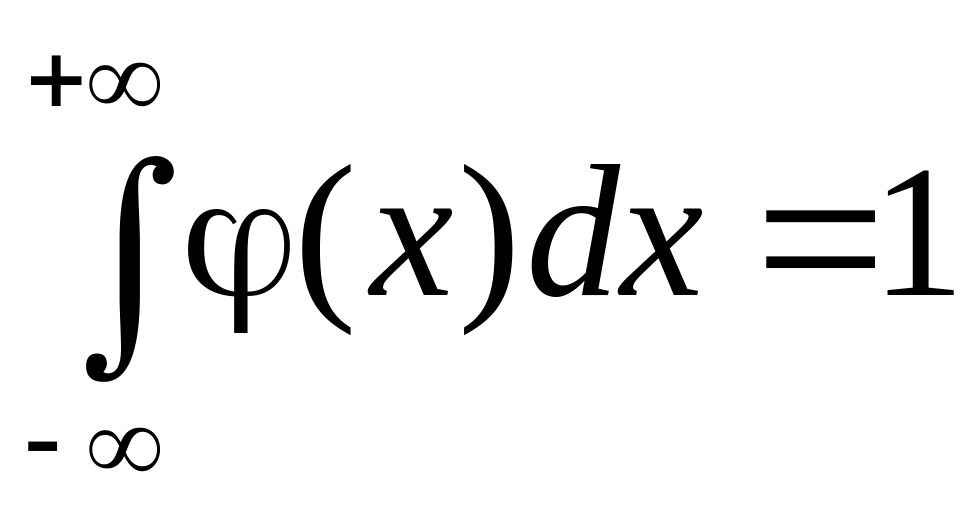 ,
т.е. площадь, ограниченная кривой
распределения и осью абсцисс,
всегда равна 1.
,
т.е. площадь, ограниченная кривой
распределения и осью абсцисс,
всегда равна 1.
Если все возможные значения случайной величины Х заключены в пределах от a до b, то второе свойство плотности примет вид:
 .
.
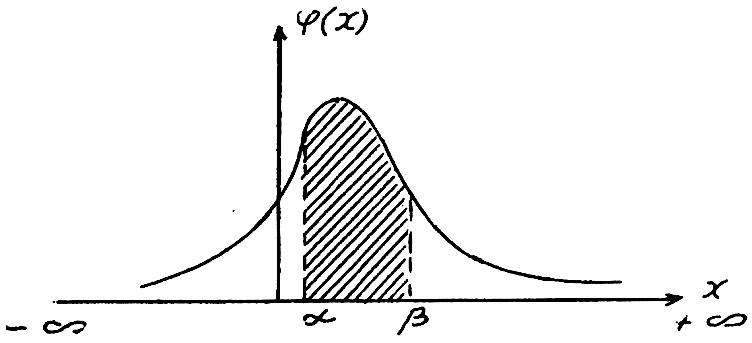
Рис. 2.4 — Кривая распределения
9) Вероятность попадания случайной величины на заданный интервал
На практике часто оказывается необходимым знать вероятность того, что случайная величина Х примет значение, заключённое в некоторых пределах, например, от до . Искомая вероятность для дискретной случайной величины Х определяется по формуле
|
|
при
этом условились левую границу
включать в участок ![]() ,
а правую β — не включать.
,
а правую β — не включать.
Для непрерывной случайной величины Х формула примет вид:
|
|
так
как вероятность любого отдельного
значения непрерывной случайной величины
равна нулю:
![]() .
.
Вероятность попадания непрерывной случайной величины Х на интервал (,) определяется также выражением:
|
|
Эта вероятность численно равна заштрихованной площади на рис. 2.4.
Выразим функцию
распределения
через плотность ![]() .
Функция распределения определяется
выражением , а, учитывая , получаем
формулу для вычисления функции
распределения непрерывной случайной
величины
.
Функция распределения определяется
выражением , а, учитывая , получаем
формулу для вычисления функции
распределения непрерывной случайной
величины
|
|
где х в верхнем пределе интегрирования представляет собой конкретное значение аргумента.
Задача 2.2. В условиях задачи 2.1 найти вероятность того, что число попаданий в мишень будет находиться в пределах от 1 до 3 (т.е. будет равно или 1, или 2).
Решение. На основании имеем
![]() .
.
Действительно,
![]() .
.
Задача 2.3. Случайная величина Х задана функцией распределения
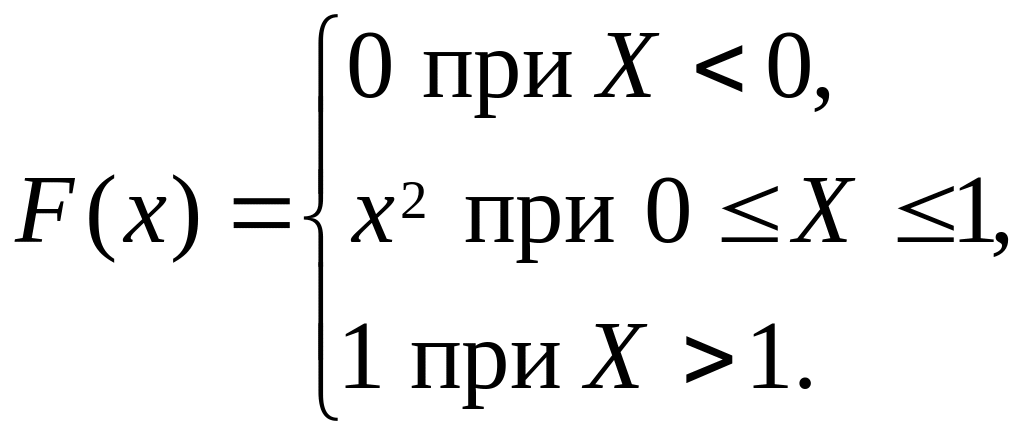
Найти
плотность
,
а также вероятность того, что в результате
испытания случайная величина Х
примет значение, заключённое в интервале ![]() .
.
Решение:
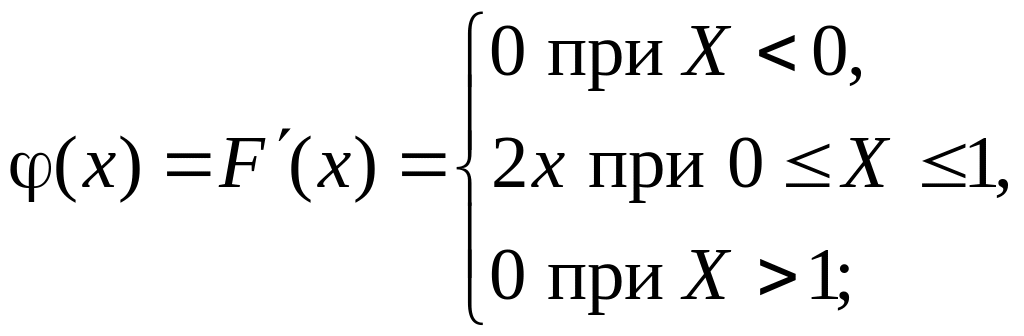
Вероятность попадания случайной величины Х в интервал определяем по формуле . Принимая
 и
и
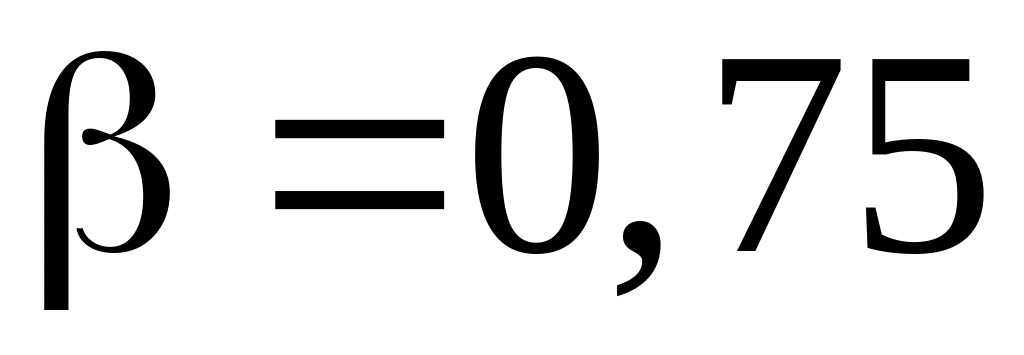 ,
находим
,
находим
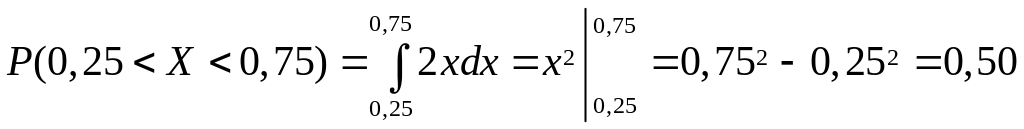
или по формуле
![]() .
.
10) Математическое ожидание и его свойства
Закон распределения характеризует полностью случайную величину с вероятностной точки зрения. Однако при решении ряда задач достаточно бывает указать только отдельные числовые параметры, характеризующие основные черты распределения; например, какое-то среднее значение (центр распределения), около которого группируются возможные значения случайной величины, или, например, число, характеризующее степень разброса этих значений относительно среднего, и т.д.
Математическое
ожидание служит характеристикой
центра распределения случайной величины.
Применяют обозначения:
![]() или
или
![]() .
.
Математическим ожиданием дискретной случайной величины Х называют сумму произведений всех её возможных значений на их вероятности
|
|
Математическое ожидание непрерывной случайной величины Х определяется по формуле
|
|
Свойства математического ожидания:
 ,
где С — постоянная величина;
,
где С — постоянная величина;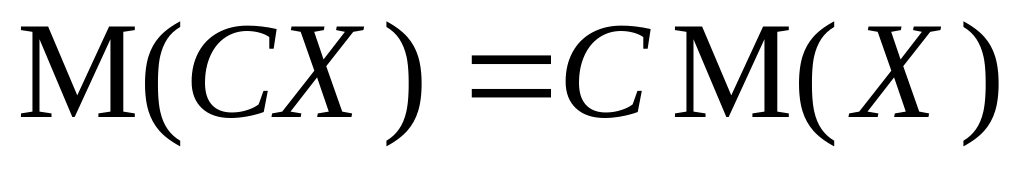
 ;
; ,
если
,
если
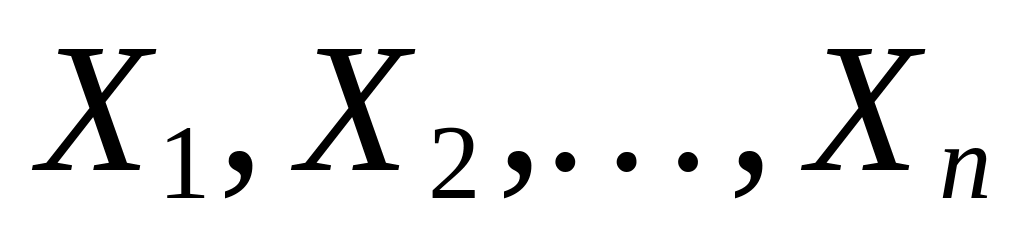 —
взаимно независимые случайные величины.
—
взаимно независимые случайные величины.

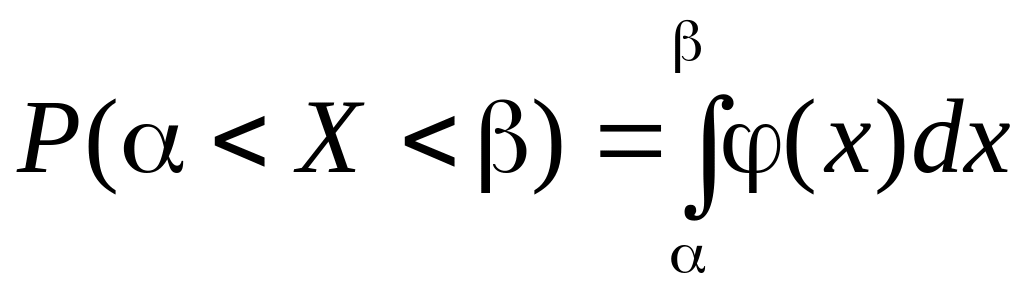 .
.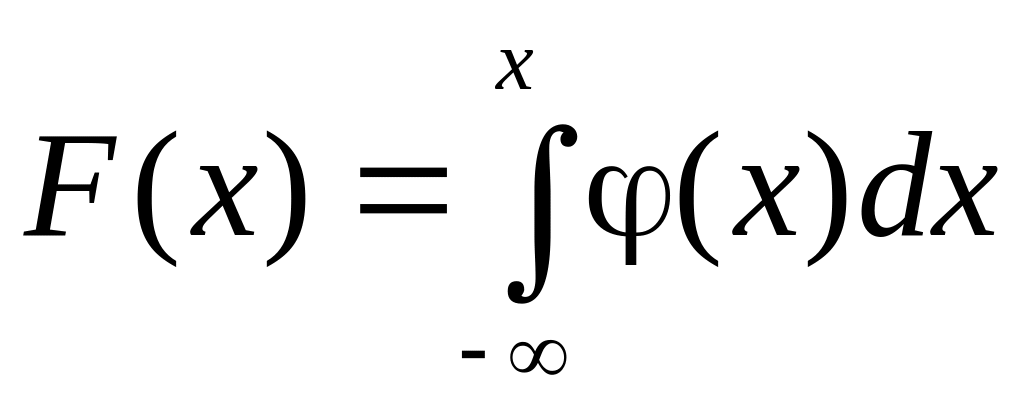 ,
,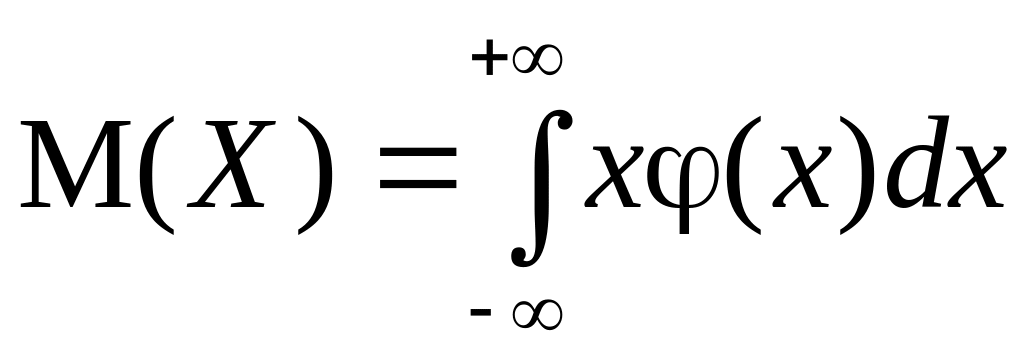 .
.