
- •2.4. Вопросы для самоконтроля 34
- •3.3. Вопросы для самоконтроля 48
- •4.3. Вопросы для самоконтроля 55
- •6.4. Вопросы для самоконтроля 89
- •Л екция 1. Вынужденные колебания стрелы мостового крана
- •1.1. Постановка задачи. Описание модели
- •1.2. Уравнения движения
- •1.3. Уравнения малых колебаний
- •1.4. Нормализация. Переход к безразмерным переменным
- •1.5. Решение уравнений вынужденных колебаний
- •1 .5.1. Случай резонанса
- •Случае ( )
- •Случае ( )
- •1.5.2. Нерезонансный случай
- •От частоты вынуждающей силы
- •1 .5.3. Биения
- •1.6. Вопросы для самоконтроля
- •Лекция 2. Линейные динамические системы
- •2.1. .Весовая матрица. Решение систем линейных дифференциальных уравнений. Теорема Коши
- •2.2. Матричная экспонента. Теорема Гамильтона-Кэли
- •2.3. Пример решения линейной системы дифференциальных уравнений
- •2.4. Вопросы для самоконтроля
- •Лекция 3. Управляемые линейные системы. Критерий управляемости калмана
- •3.1. Представление решения линейной управляемой системы с помощью матричной экспоненты. Матрица управляемости Калмана
- •3.2. Доказательство критерия управляемости Калмана
- •3.3. Критерий управляемости Калмана для систем со скалярным управлением
- •3.3. Вопросы для самоконтроля
- •Лекция 4. Управляемые линейные системы. Критерий управляемости хаутуса
- •4.1. Критерий управляемости Хаутуса
- •4.2. Критерий управляемости для линейных систем второго порядка
- •4.3. Вопросы для самоконтроля
- •Лекция 5. Задача одновременного управления двумя маятниками
- •5.1. Уравнения движения системы двух маятников
- •5.2. Анализ управляемости системы по критерию Калмана
- •5.3. Анализ управляемости системы по критерию Хаутуса
- •Лекция 6. Синтез управления в задаче о стабилизации маятника в верхнем положении равновесия
- •6.1. Фазовая плоскость. Типы особых точек линейного дифференциального уравнения второго порядка
- •6.1.1. Центр
- •6.1.2. Устойчивый фокус
- •6.1.3. Неустойчивый фокус
- •6.1.4. Седло
- •6.1.5. Устойчивый узел
- •6.2 Задача управления колебаниями маятника около верхнего положения равновесия. Синтез управления при наличии ограничения на управление. Построение области управляемости
- •6.3. Синтез управления при наличии ограничения на управление. Метод выделения неустойчивой координаты
- •6.4. Вопросы для самоконтроля
1 .5.1. Случай резонанса
Так,
если
собственная
частота
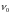 колебаний груза совпадает с частотой
колебаний груза совпадает с частотой
 изменения внешней силы, то есть, если
изменения внешней силы, то есть, если
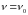 ,
имеет
место внешний резонанс.
,
имеет
место внешний резонанс.
В этом случае интеграл 124 будет равен
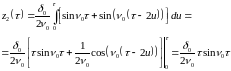 25125\* MERGEFORMAT (.)
25125\* MERGEFORMAT (.)
Очевидно, что амплитуда колебаний груза в резонансном случае линейно возрастает со временем.
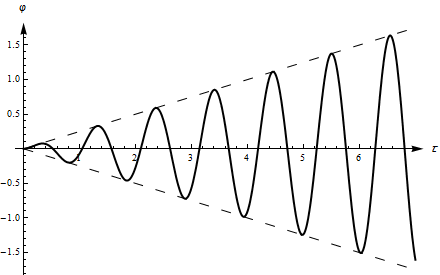
Рис.2 Изменение угла отклонения стрелы в резонансном
Случае ( )
Оглавление
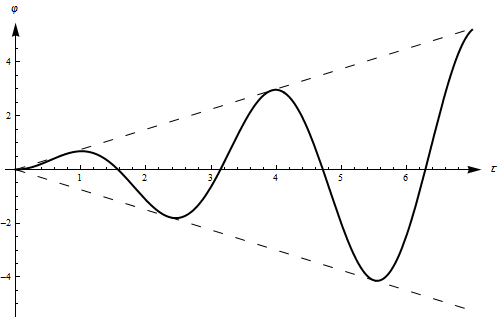
Рис.3 Изменение угла отклонения стрелы в резонансном
Случае ( )
Графики
зависимости колебаний стрелы в резонансном
случае представлены на рис. 2, 3. График
на рисунке 2 построен для значений
и
частота 120
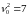 ,
на рисунке 3, соответственно,
и
,
на рисунке 3, соответственно,
и
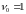 .
.
1.5.2. Нерезонансный случай
Если собственная частота и частота изменения внешней силы не совпадают, то вычисление интеграла 124 дает
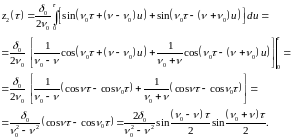 26126\* MERGEFORMAT (.)
26126\* MERGEFORMAT (.)
Оглавление
Таким образом, вынужденные колебания стрелы мостового крана в нерезонансном случае происходят по закону
 27127\* MERGEFORMAT (.)
27127\* MERGEFORMAT (.)
Полученное
решение уравнений вынужденных колебаний
представляет собой сумму частного
решения уравнения собственных колебаний
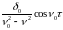 и частного решения уравнения вынужденных
колебаний
и частного решения уравнения вынужденных
колебаний
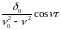 .
Такая сумма уже не будет не только
гармоническим колебанием, но и, вообще
говоря, при произвольных значениях
и
периодической функцией. Графики решения
для различных значений частот
.
Такая сумма уже не будет не только
гармоническим колебанием, но и, вообще
говоря, при произвольных значениях
и
периодической функцией. Графики решения
для различных значений частот
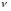 и
приведены на рисунках 4, 5.
и
приведены на рисунках 4, 5.
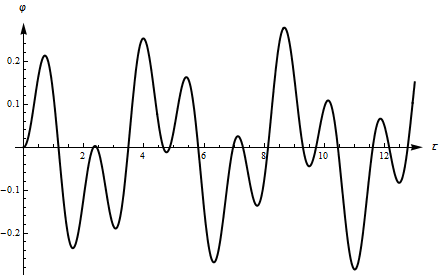
Рис.4
Изменение угла
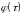 в нерезонансном случае
в нерезонансном случае
Оглавление
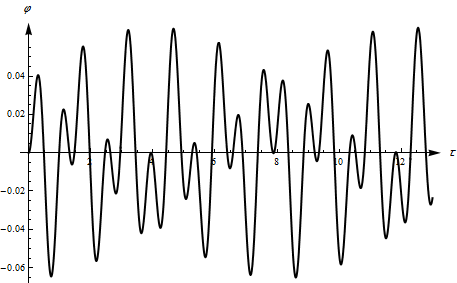
Рис.5 Изменение угла в нерезонансном случае
Амплитуда
вынужденных колебаний, как это видно
из 127, обратно пропорциональна разности
 ,
то есть, тем больше, чем ближе значения
собственной частоты и частоты вынуждающей
силы. График зависимости модуля амплитуды
вынужденных колебаний от частоты
вынуждающей силы (АЧХ) приведен на
рисунке 6.
,
то есть, тем больше, чем ближе значения
собственной частоты и частоты вынуждающей
силы. График зависимости модуля амплитуды
вынужденных колебаний от частоты
вынуждающей силы (АЧХ) приведен на
рисунке 6.
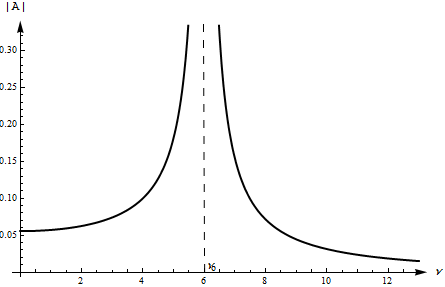
Рис.6 Зависимость модуля амплитуды вынужденных колебаний
От частоты вынуждающей силы
Оглавление
1 .5.3. Биения
Характерный вид имеет решение 127 уравнений вынужденных колебаний в случае, когда собственная частота и частота изменения внешней силы имеют близкие значения.
Как это видно из формулы 126
 28128\* MERGEFORMAT (.)
28128\* MERGEFORMAT (.)
Зависимость
может быть представлена в виде произведения
двух гармонических функций с существенно
различающимися частотами
 и
и
 .
Малая частота
.
Малая частота
 называется несущей частотой. Большая
частота
называется несущей частотой. Большая
частота
 называется частой модуляции. Соответствующие
периоды равны
называется частой модуляции. Соответствующие
периоды равны
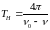 ,
,
 .
.
При
малых значениях параметра
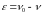 ,
справедливы приближённые соотношения
,
справедливы приближённые соотношения
 29129\* MERGEFORMAT (.)
29129\* MERGEFORMAT (.)
Графики изменения переменной при близких значениях собственной и вынуждающей частот приведены на рисунках 7, 8. Такой вид колебаний называется биениями. Аналогичные режимы наблюдаются также в системах со многими степенями свободы в случае близких значений собственных частот.
Оглавление
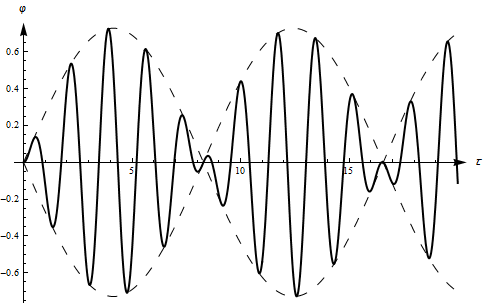
Рис.7
Биения

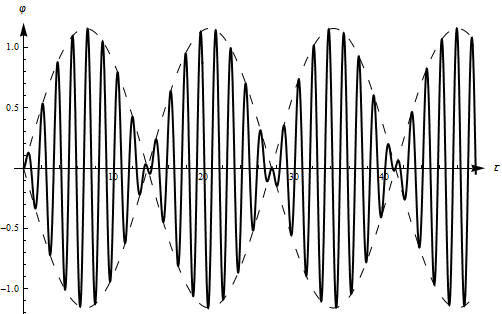
Рис.8
Биения

1.6. Вопросы для самоконтроля
Какие уравнения описывают вынужденные, а какие уравнения описывают свободные колебания механической системы?
Что такое характеристическое уравнение линейного дифференциального уравнения?
Дайте определение весовой функции линейного дифференциального уравнения. Каким начальным условиям удовлетворяет весовая функция?
Оглавление
Сформулируйте теорему Коши о частном решении неоднородного линейного дифференциального уравнения.
Какой вид имеет общее решение линейного неоднородного дифференциального уравнения?
Сформулируйте условие возникновения резонансных режимов колебаний. Какой вид имеет решение линейного дифференциального уравнения второго порядка в случае резонанса?
Являются ли вынужденные колебания при произвольных начальных условиях гармоническими?
Когда в линейной системе с одной степенью свободы возникают биения?
302Equation Section (Next)
Оглавление
