7.3.6 Построение эпюры арматуры для изгибаемых железобетонных элементов

Эпюрой арматуры условно принято называть диаграмму распределения площадей поперечных сечений продольной арматуры элемента по его длине с учетом обрыва некоторых стержней для экономии материала. Эта эпюра позволяет дать, количественную оценку превышения величины изгибающего момента, соответствующего принятой площади сечения арматуры, по отношению к теоретическому значению расчетной величины изгибающего момента. Поскольку превышение фактически означает установку излишней арматуры, то это превышение необходимо свести к минимуму. Практически излишнюю арматуры обрывают в пролете в сечениях так называемого теоретического обрыва арматуры.

Порядок определения положения сечений теоретического обрыва заключается в следующем (рис.1.35):

- выполняют построение эпюры расчетных изгибающих моментов от внешней расчетной нагрузки;

- выполняют построение эпюр площадей поперечных сечений продольной рабочей арматуры, которую обрывают в пролете и доводят до торца элемента не менее двух стержней и не менее 50% от общего числа стержней в пролете;

- выполняют построение эпюры огибающих предельных моментов, вычисляя предельный изгибающий момент для каждого из двух участков пролета элемента, используя формулу

,

откуда , (1.107)

где A_si – площади поперечных сечений продольной арматуры на расчетном участке;

z_i – плечо момента, создаваемого усилием продольной арматуры относительно горизонтальной центральной оси для сжатой от внешних нагрузок зоне поперечного сечения;

- находят координаты точек пересечения эпюры огибающих предельных моментов (M_ui) с эпюрой расчетных изгибающих моментов, то есть определяют положение сечений теоретического обрыва арматуры;

- обрываемые арматурные стержни заводят за сечения теоретического обрыва на длину, определяемую по эмпирической формуле вида:

, (1.108)

где Q – поперечная сила в нормальном сечении теоретического обрыва стержней;

q_sw – погонное усилие от хомутов, определяемое на длине шага S_w по формуле (1.95);

A_s,inc – общая площадь отгибов арматуры в наиболее нагруженном сечении;

θ – угол наклона отгибов к оси элемента;

d_s – диаметр обрываемого стержня рабочей продольной арматуры.

Если отгибы отсутствуют (т.е. A_s,inc =0), то формула (1.108) принимает вид

, (1.108а)

Если отсутствует и поперечная арматура, то следует принять руководствуясь нормативными требованиями.

С учетом сказанного, примерная схема эпюры материала приведена на рис.1.35.

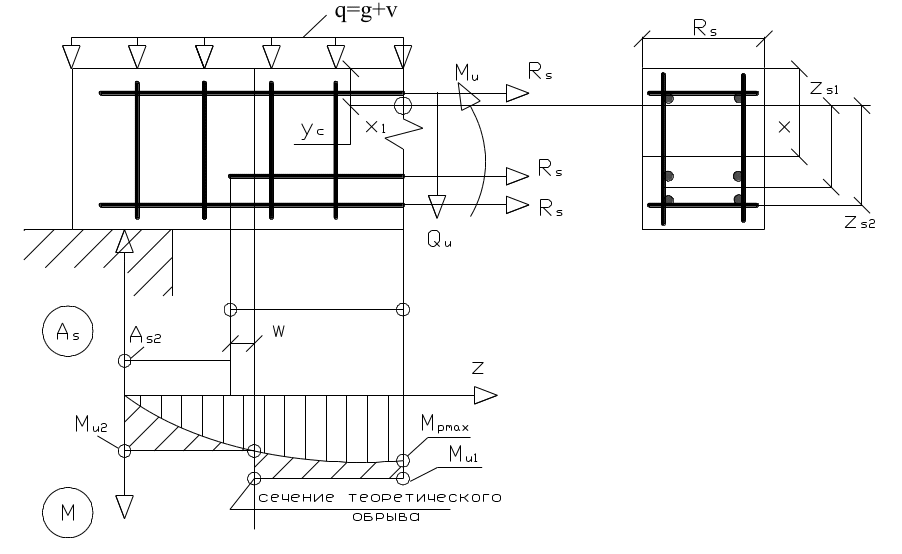
Рис.1.35. Схема построения эпюры материла

Чем меньше площадь фигуры, определяющей превышение эпюры М_u над эпюрой М_р, тем меньше расход материала при одинаковой несущей способности элемента. Поэтому в растянутой зоне изгибаемого элемента рекомендовано нормами устанавливать не менее четырех стержней, чтобы два из них можно было оборвать в пролете, тем самым более полно использовать несущую способность установленной арматуры.

7.4 Расчет на прочность внецентренно сжатых элементов

7.4.1 Основные положения расчета

Внецентренно сжатыми считают элементы (колонны, перегородки и стенка зданий, элементы ферм и арок), на которые расчетные продольные сжимающие силы (N) действуют с начальным эксцентриситетом (е₀) по отношению к геометрической оси элемента. К этой же категории относят элементы, на которые действуют одновременно осевая продольная сжимающая сила (N) и изгибающий момент (М) (см.рис.1.36)

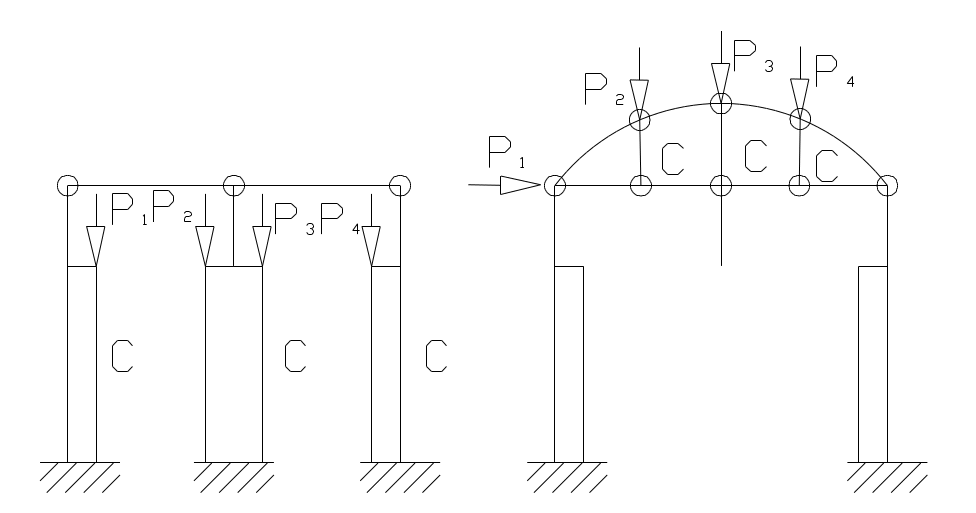
Рис.1.36. Примеры элементов конструкций, работающих на сжатие

с – сжатый элемент

Так называемое центральное сжатие встречается весьма редко. Его трудно реализовать даже в лабораторных условиях, поэтому в расчетах всегда принимают величину так называемого случайного эксцентриситета (е₀), обусловленного наличием случайных факторов (неоднородность бетона, допуски формы и размеров и т.д.).

Нормативно (см.п. 4.2.6 СП52-101-2003) установлена величина случайного эксцентриситета в виде большего из трех значений:

, (1.109)

где L – длина рассчитываемого элемента (или части элемента между ближайшими закрепленными сечениями);

h – высота поперечного сечения элемента.

Для статически определимых конструкций при одновременном действии расчетной сжимающей осевой силы и расчетного изгибающего момента вводят понятие начального эксцентриситета (е₀), определяемого по схеме рис.1.37.

Рис.1.37. Расчетная схема для определения начального эксцентриситета (е₀)

Тогда для статически определимых систем общий эксцентриситет определяют в виде:

, (1.110)

по значению которого и выполняют расчет.

При расчете статически неопределимых систем из значений (е_а) и (е₀) принимают большее (см.п. 4.2.6. СП 52-101-2003).