1.6. Сложная функция

Пусть задана функция c множеством определения и множеством значений , и функция y=f(u), областью определения которой является , а множеством значений E(f). Тогда на множестве определена сложная функция (или суперпозиция функций, или функция от функции) с множеством значений E(f). Записывается сложная функция . Переменная называется промежуточным (или внутренним) аргументом функции.

Например: - синус квадрата.

1.7. Обратная функция

Пусть задана функция y=f(x) c областью определения D(f), множеством значений E(f). Если каждому значению соответствует единственное значение , то определена обратная функция (которая иногда обозначается ) с областью определения E и множеством значений D. Про такие функции y=f(x) и говорят, что они взаимно обратные. Для того, чтобы найти функцию , достаточно разрешить уравнение y=f(x) относительно переменной x.

Строго монотонная функция имеет обратную, причем если сама функция возрастает ( убывает), то и обратная так же возрастает( убывает).

Графики функций y=f(x) и изображаются одной и той же кривой. Если же в обратной функции независимую переменную назвать х , а зависимую у, то графики двух взаимно обратных функций y=f(x) и симметричны относительно биссектрисы 1-3 координатных углов.

Пример: Графики двух взаимно- обратных функций -синий и - зеленый.

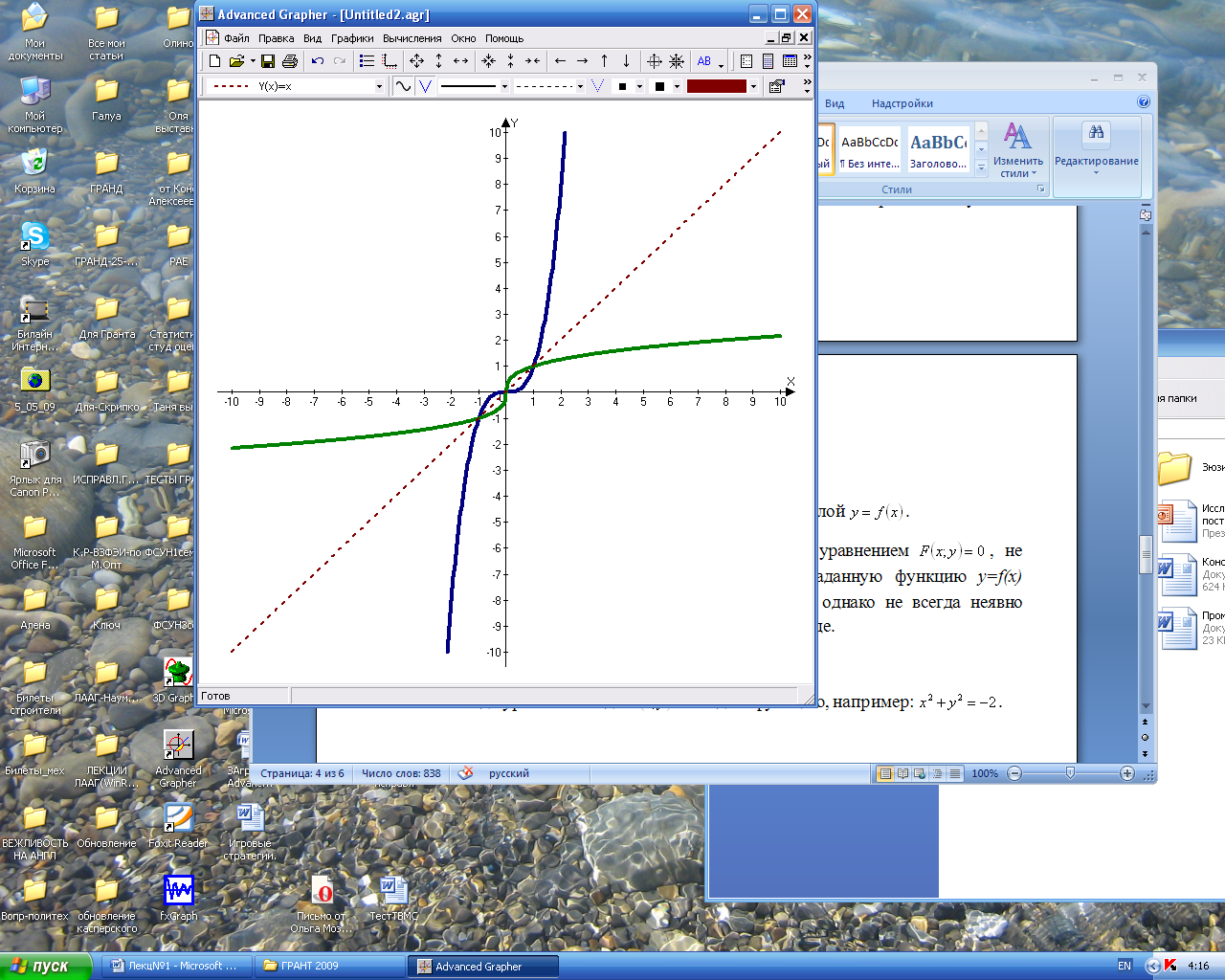
1.8. Неявная функция

Функция называется явной, если она задана формулой .

Функция называется неявной, если она задана уравнением , не разрешенным относительно . Любую явно заданную функцию y=f(x) можно представить в неявном виде: y-f(x)=0 , однако не всегда неявно заданную функцию можно представить в явном виде.

Пример неявно заданной функции: .

Примеры:

1. Найти область определения функции:

2. Найти множество значений функции:

3. Писать четные функции из данных:

4. Выписать периодические функции:

5. Даны две функции: составить сложные функции:f(g(x)) и g(f(x)).

6. Найти обратную функцию для данной:

Ответы:

1. (D(f)=(

2. (E(f)= )

3. 

4. (

5. (f(g(x))= и g(f(x))= .)

6. (

Лекция № 2 Последовательность. Предел числовой последовательности

2.1. Бесконечная числовая последовательность

Опредедение.1 Бесконечной числовой последовательностью называется числовая функция, определенная на множестве N натуральных чисел.

Опредедение.2 Последовательность называется возрастающей (убывающей), если каждый ее член, начиная со второго, больше (меньше) предыдущего, т. е. если для любого n выполняется неравенство > ( < ).

Опредедение.3 Последовательность называется невозрастающей (неубывающей), если каждый ее член, начиная со второго, не больше (не меньше) предыдущего, т.е. если для любого п выполняется неравенство .

Убывающие, возрастающие, неубывающие и невозрастающие последовательности называются монотонными.

Опредедение.4 Последовательность называется ограниченной сверху (ограниченной снизу), если можно указать такое число М (число т), что для всех членов этой последовательности выполняется неравенство М ( т). Числа М и т называются соответственно верхней и нижней границами последовательности . Тот факт, что последовательность ограничена сверху числом М (снизу числом т) геометрически означает, что ни одна точка не лежит правее точки М (левее точки т).

Опредедение.5 Последовательность называется ограниченной, если существуют два числа т и М такие, что для всех n выполняется неравенство т М. Тот факт, что последовательность ограничена числами т и М, геометрически означает, что все её члены помещаются в промежутке [т, М].

Опредедение.6 Последовательность называется постоянной, если все ее члены совпадают.

Обычно последовательность задается формулой, выражающей общий член последовательности через n. Иногда указывается правило, по которому можно вычислить n-й член последовательности по ее известным предыдущим членам, такой способ задания последовательности называется индуктивным (или рекуррентным).