
- •1.3. Функции, способы задания, свойства
- •1.Табличный, когда значения аргумента и соответствующие значения функции заданы таблицей.
- •2.Графический, когда соответствие аргумента и функции даны в виде графика;
- •3.Аналитический, когда зависимость дана в виде формулы.
- •1.4. Основные свойства функции:
- •1.5.Основные элементарные функции и их области определения
- •Функция определена на общей области определения функций f(X) и g(X), при условии, что g(X)≠0.
- •1.6. Сложная функция
- •1.7. Обратная функция
- •Пример: Графики двух взаимно- обратных функций -синий и - зеленый.
- •Лекция № 2 Последовательность. Предел числовой последовательности
- •2.1. Бесконечная числовая последовательность
- •2.2.Примеры
- •2. Написать общий член последовательности натуральных чисел, каждое из которых при делении на 3 дает остаток, равный 1.
- •3. Последовательность задана рекуррентным соотношением . Найти первые члены последовательности.
- •5. Доказать, что последовательность ограничена снизу и сверху.
- •2.3. Предел числовой последовательности
- •2.4. Теоремы о пределах
- •2.5. Предельный переход в неравенствах
- •2.6. Бесконечно малые и бесконечно большие последовательности
- •Лекция № 3 Предел функции
- •3.1.Определение предела функции
- •3.6. Связь между функцией, ее пределом и бесконечно малой функцией
- •3.10. Теорема о пределе монотонной функции
- •3.11. Некоторые обозначения
- •Примеры
- •Лекция № 4 Первый и второй замечательные пределы
- •4.1.Теорема (первый замечательный предел)
- •2) Пусть , тогда при .
- •4.2. Примеры
- •4.3. Второй замечательный предел. Число e.
- •4.4. Примеры
- •4.5. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции
- •4.6. Теоремы об эквивалентных бесконечно малых функциях
- •1) Функция f(X) определена в точке х0 и ее окрестности;
- •2) Функция f(X) имеет предел при х→х0 ;
- •3) Предел функции в точке х0 равен значению функции в этой точке.
- •5.2. Непрерывность функции в интервале и на отрезке
- •5.3. Точки разрыва и их классификация
- •2) Если , то х0 называется точкой конечного разрыва, а величину называют скачком функции.
- •5.4. Основные теоремы о непрерывных функциях
- •5.5. Свойства функций, непрерывных на отрезке
- •Вычислить
- •Если , то х найден, иначе идти на пункт 2.
- •6.2. Связь между непрерывностью и дифференцируемостью
- •6.3. Геометрический смысл производной
- •6.4. Основные правила дифференцирования
- •Правила дифференцирования:
- •6.5. Производная обратной функции
- •6.6. Производная неявно заданной функции
- •6.7. Производная показательно- степенной функции
- •6.8. Производная функции, заданной параметрически
- •Лекция № 7 Дифференциал функции
- •7.1. Понятие дифференциала
- •7.2.Геометрический смысл дифференциала
- •3. , Тогда
- •Лекция №8 Теоремы о дифференцируемых функциях
- •8.1. Теорема Ролля.
- •Найдём производную в точке
- •8.2. Теорема Коши
- •8.3. Теорема Лагранжа
- •8.4. Правило Лопиталя
- •Правило Лопиталя раскрытия неопределённостей вида
- •8.5. Правило Лопиталя для раскрытия неопределенности вида
- •Теорема остается справедливой и в том случае, если х ® ±¥ или х®х0±0;
- •Если опять дает неопределенность вида или , то правило Лопиталя следует применить еще раз.
- •Лекция № 9 Исследование функции и построение графика
- •9.1. Возрастание и убывание функции.
- •9.2. Интервалы монотонности функции
- •Теорема (необходимые условия монотонности):
- •Теорема (достаточные условия монотонности):
- •9.3. Экстремумы функции
- •Для исследования функции на экстремум, необходимо:
- •Исследовать знак производной f´(X) слева и справа от критических точек ( или исследовать знак второй производной в этих точках)
- •С помощью теорем о достаточном условии экстремума определить характер экстремума и вычислить его значение.
- •9. 4. Выпуклость графика функции. Точки перегиба.
- •9.5. Асимптоты графика функции.
- •9.6. Общая схема исследования функции и построения графика.
- •4. Найдем асимптоты графика функции.
- •5 . Для нахождения точек возможного экстремума найдем производную функции:
- •6. Для нахождения точек перегиба и интервалов выпуклости, вогнутости найдем вторую производную функции:
6.3. Геометрический смысл производной
К асательной
к данной кривой в данной точке М называется
предельное положение МТ секущей MN,
проходящей через точку М, когда вторая
точка секущей N,
неограниченно приближается по кривой
к точке М.
асательной
к данной кривой в данной точке М называется
предельное положение МТ секущей MN,
проходящей через точку М, когда вторая
точка секущей N,
неограниченно приближается по кривой
к точке М.
Рассмотрим график
непрерывной функции y=f(x).
Пусть в точке
функция имеет невертикальную касательную
(предельное положение секущей). Найдем
угловой коэффициент секущей k=tg
,
где
-
угол наклона касательной к оси ОХ.
Угловой коэффициент секущей ![]()
При ![]() стремящемся к нулю,
стремящемся к нулю,
![]()
![]() .
.
![]() -
угловой коэффициент касательной.
-
угловой коэффициент касательной.
Если функция
y=f(x)
имеет невертикальную касательную в
точке
,
то в этой точке существует производная
![]() ,
равная тангенсу угла наклона касательной
к графику функции в точке
к оси
,
равная тангенсу угла наклона касательной
к графику функции в точке
к оси
![]() .
.
Справедливо и обратное утверждение:
Если функция
![]() имеет производную в точке
,
то график функции имеет невертикальную
касательную, тангенс угла наклона
которой к
равен
.
имеет производную в точке
,
то график функции имеет невертикальную
касательную, тангенс угла наклона
которой к
равен
.
Уравнение
касательной
к графику
функции в точке с абсциссой
,
имеет вид:
![]() .
.
Нормаль-это прямая, проходящая через точку касания и перпендикулярная касательной.
Уравнение нормали:
![]() .
.
Пример:
Составить
уравнения касательной и нормали к
графику кривой у = 2![]() в точке с абсциссой х0
=
в точке с абсциссой х0
=
![]() .
.
Решение:
у/ =
 ((3-х2)/2)/
=
((3-х2)/2)/
=
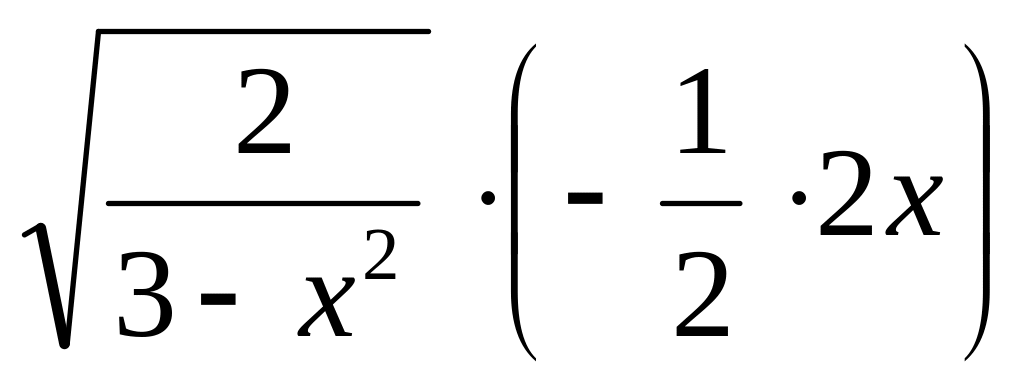 = -
= -
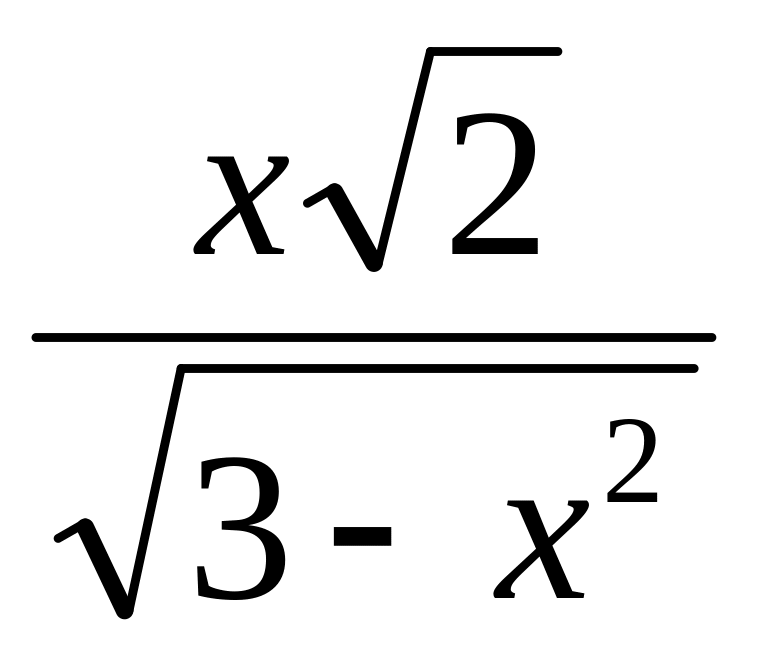 .
.у/(х0) = у/( ) = - 2.
у(х0) = у( ) = .
Тогда уравнения касательной и нормали имеют вид:
у - = - 2(х - ) Þ 2х + у - 3 = 0 – искомое уравнение касательной;
у -
=
![]() (х
-
)
Þ
х – 2у +
= 0 – искомое уравнение нормали.
(х
-
)
Þ
х – 2у +
= 0 – искомое уравнение нормали.
6.4. Основные правила дифференцирования
Производная постоянной величины равна
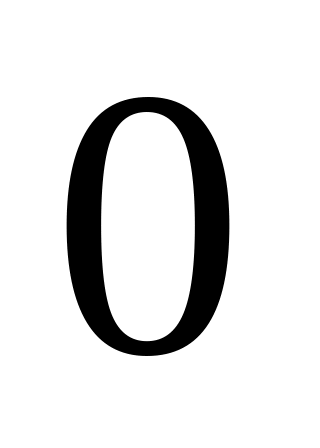 .
.
Доказательство:
Дадим приращение
![]() ,
,
![]() .
.
![]()
![]() .
.
2.Производная суммы двух функций равна сумме производных.
![]() .
.
Доказательство:
![]() ,
если
,
если
![]() и
и
![]() -
дифференцируемые функции, то их
алгебраическая сумма дифференцируема.
-
дифференцируемые функции, то их
алгебраическая сумма дифференцируема.
![]() .
.
![]() По определению
производной:
По определению
производной:
![]() .
.
3. Производная произведения двух функций:
![]() .
.
Пример: Найти производную функции:
у = соsxln2x.
y/ = (cosx)/ ln2x + cosx (ln2x)/ = - sinx ln2x + cosx2lnx(lnx)/ =
- sinxln2x
+cosx2lnx(![]() ).
).
4. Производная частного:
Если
и
-
дифференцируемые и
![]() ,
то
,
то
![]()
Пример: Найти производную функции:
y
=
![]()
y/
=
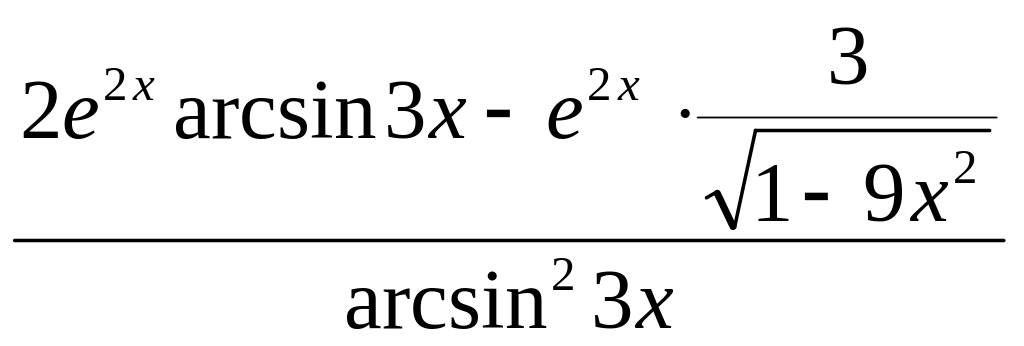
Производная сложной функции:
Если
![]() и
и
![]() -
дифференцируемые функции от своих
аргументов, то производная сложной
функции
-
дифференцируемые функции от своих
аргументов, то производная сложной
функции
![]() существует и равна
существует и равна
![]() .
.
Доказательство:
Дадим
отличное от нуля приращение
![]() ,
тогда
получит приращение
,
тогда
получит приращение
![]() ,
-
приращение
,
-
приращение
![]() .
.
По условию
![]()
![]() .
.
![]() .
Перейдем к пределу
.
Перейдем к пределу
![]()
![]()
![]()
![]()
![]() -
дифференцируема,
-
дифференцируема,
![]() непрерывна в точке
непрерывна в точке
![]()
![]() .
.
Правила дифференцирования:
С/ = 0
(CU)/ = CU
(U±V)/ = U/ ± V/
(UV)/ = U/V + UV/
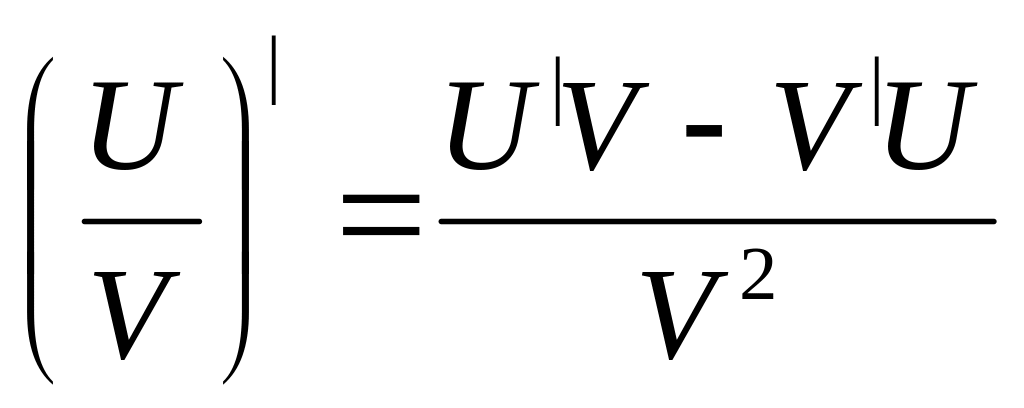 при V¹0.
при V¹0.
Таблица производных
|
(Un)|
= n
|
(au)/ = au ×ln a× U/
|
(eu)/ = eu × U/
|
(sin U)/ = cos U × U/
|
(cos U)/ = -sin U× U/
|
(tg U)/
=
|
(ctg U)/
=
|
(arcsin
U)/
=
|
(arcos
U)/
=
|
(arctg
U)/
=
|
(arcctg
U)/
=
|
(log a
U)/
=
|
(lnU)/
=
|
