36. Уравнение поверхности уровня

Поверхностью уровня называют такую поверхность, во всех точках которой давление одинаково (dP=0)

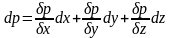
то, с учетом уравнение Эйлера:

для поверхности уровня:

В случае идеальной жидкости:

Пример:

Пусть жидкость покоится в поле тяготения 3емли.

Плоскость 0XY горизонтальна, а ось z направлена вертикально вверх. В этом случае:

Тогда:

т.е. z=const, т.о. поверхности уровня (в частности, свободная поверхность) горизонтальны.

37. Закон паскаля

Жидкость покоится в поле тяготения Земли. В этом случае уравнения Эйлера имеют вид:

(282)

(283)

( 284)

С учетом (282) и (283) последнее уравнение (284) принимает вид:

(285)

откуда:

(286)

где удельный вес жидкости. Интегрируя (286), получаем

(287)

Постоянная интегрирования будет определена, если в точке с координатой z₀ известно давление p₀ . Тогда

Последнее выражение обычно записывают в виде:

(288) т.е. для жидкости, покоящейся в поле тяготения Земли, сумма геометрической (Z) и пьезометрической (p/)) высот для всех точек объема жидкости одинакова. Это и есть закон Паскаля.

38. Сообщающиеся сосуды заполнены однородной жидкостью

Свободные поверхности в левом и правом коленах находятся на уровнях Z₁ и Z₂, а давление на этих поверхностях равно атмосферному Р_a. Сравним свободные поверхности с общей для обоих сосудов частью, уровнем Z₀, на котором давление равно P₀, как показано на рис. 71.

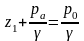
Откуда:

(рис. 71)

Следовательно, свободные поверхности устанавливаются на одном уровне.

39. Закон архимеда Тело погружено в жидкость (рис. 73).

Рис.73.

На его поверхность со стороны жидкости действуют силы давления, выделим в теле объем малого сечения, ось которого вертикальна. На верхнюю и ниж­нюю грани этого объема действу­ют силы давления:

Равнодействующая сил давле­ния в проекции на вертикальную ось равна:

где: dS - проекция dS₁ (или dS₂) на горизонтальную плоскость. Разность давлений по закону Паскаля равна

где: dZ - разность уровней центров граней выделенного объема. Тогда равнодействующая сил давления равна

где dV - величина выделенного объема.

Вертикальная проекция сил давления, действующих на всю смоченную поверхность тела, может быть получена путем интегри­рования предыдущего выражения:

т.е. сила, действующая со стороны жидкости на погруженное в нее тело по величине равна весу жидкости, вытесненной телом.

Формулировка закона: на тело, погруженное в жидкость действует выталкивающая сила, равная весу жидкости в объеме, вытесненном телом , и приложенная в той точке смоченной поверхности тела, в которой вертикаль, проведенная через центр масс вытесненной жидкости, пересекает эту поверхность.

Существенным в формулировке закона Архимеда является правильное указание точки приложения выталкивающей силы. Действительно, поскольку сила Архимеда обусловлена действием рас­пределенных по поверхности сил давления со стороны жидкости, то и равнодействующая сил давления должна быть приложена к смоченной поверхности тела (но не к центру масс вытесненной жидкости, как это часто утверждается). Кроме того, наличие в плавающем теле деформаций можно объяснить только при таком рассмотрении силы Архимеда.