33.1 Гироскопы.

Рассмотрим быстро вращающийся относительно оси симметрии массивный диск (рис.64). При очень быстром вращении диска, как было сказано выше, векторы момента импульса и угловой скорости направлены вдоль оси симметрии.

Если к концам оси вращения приложить пару сил, ее момент будет изменять момент импульса в соответствии с уравнением моментов:

рис. 64)

Через промежуток времени 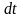момент импульса изменит свое направление и станет равным Соответственно изменится и положение оси симметрии. Как видно, силы пары приложены в горизонтальной плоскости, а ось вращается под действием момента - в вертикальной.

Уравнение моментов в скалярном виде в этом случае представляют следующим образом:

С учетом направлений векторов уравнение моментов для быстро вращающегося тела записывает в векторной форме так:

(273)

Гироскопом называют массивное тело, очень быстро вращающееся вокруг оси симметрии. Наиболее часто применяются гироскопы в кардановых подвесах. В таких подвесах при любом повороте оси вращения центр масс гироскопа остается неподвижным (рис.65) Нa рисунке представлен карданов подвес для гироскопа с двумя степенями свободы.

Рис.65

Для определения угловой скорости прецессии удобно пользоваться следующими соображениями. Масштаб измерения можно выбрать таким, что конец вектора совпадает с концом оси гироскопа (рис. 66).

(рис. 66)

При действии на конец оси (в т. А) силы ее момент вызовет прецессион­ное вращение. По уравнению моментов

Но 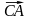можно рассматривать как радиус-вектор т. A относительно центра масс. Тогда, по определению:

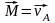(274)

33.2 Прецессия волчка.

Быстро вращающийся симметричный волчок установлен на горизонтальную поверхность (рис. 67). Точка касания неподвижна. Прецессия волчка вызывается моментом силы тяжести так как линия действия реакции проходит через неподвижный центр .

при указанном направлении вращения момент силы тяжести вызывает пре­цессию в направлении, указанном на рисунке. Угловую скорость прецессии

(рис. 67)

можно определить, пользуясь (274):

т.е.

(275)

Следовательно, угловая скорость прецессии тем меньше, чем больше угловая скорость собственного вращения.

34.1Давление покоящейся жидкости.

(рис.68)

Таким образом, коэффициенты Фурье при чётных значениях равны

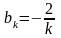(358)

а при нечётных

(359)

С учётом найденных коэффициентов (352),(356),(358), и (359) разложение в тригонометрический ряд Фурье колебаний пилообразной формы записывается в виде

(360)

в) Колебания треугольной формы

Колебания треугольной формы (рис.112) описываются функцией , определённой в промежутке и , определённой в промежутке . Так как 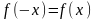, функция является чётной, а для чётной функции по (346)

(361)

Прежде всего определим по (345) значение постоянного члена разложения:

(362)

Определяем далее по (343) коэффициенты :

В этом выражении значения интегралов находим по правилу интегрирования по частям, как в предыдущем случае:

Для чётных значений

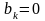
а для нечётных Используя найденные значения коэффициентов , и, записываем разложение Фурье для колебаний треугольной формы в виде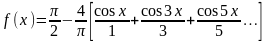

35. УРАВНЕНИЕ ГИДРОСТАТИКИ ЭЙЛЕРА

В покоящейся жидкости выделим малый ее объем dV=dxdydz в фор­ме прямоугольного параллелепипеда (рис. 70).

Известно давление в центре объема p и изменение давления на единицу длины в каждом из координат­ных направлений:

На каждую грань объема действуют силы давления, а на весь объем - объемные (массовые) силы, например, сила тяжести. Поскольку объем покоится, сумма проекции всех сил по каждому из координатных направлений равна нулю.

На заднюю грань действует сила давления:

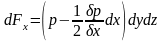
а на переднюю:

Кроме того, в этом направлении действует составляющая мас­совой силы d, которую можно определить по второму закону Ньютона:

где:  - плотность среды, a_x- ускорение, которое способна сообщить массовая сила. Т. к. объем покоится,

т.е.

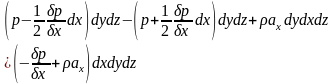
Поскольку :

(277)

Аналогично для других координатных направлений:

(278)

(279)

(277), (278), (279) и представляют собой систему уравне­ний гидростатики Эйлера.