26.1Деформация сдвига

Деформация сдвига возникает при действии на тело касательных усилий (рис. 49). Если к верхней грани образца, имеющего форму параллелепипеда, приложена касательная сила , распределённая по грани площади , грань сдвигается на расстояние , которое называется абсолютной деформацией при сдвиге.

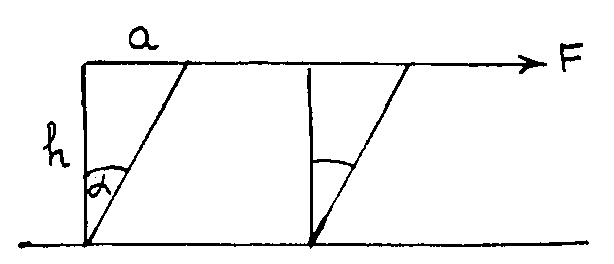(рис 49)

Относительной деформацией называют отношение абсолютной деформации к поперечным размерам . Для сдвига закон Гука принимает форму:

(208)

где 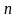-коэффициент сдвига, определяемый свойствами материала образца, величина, обратная , называется модулем сдвига:

Поскольку упругие деформации, для которых формулируется закон Гука, имеют место только при маленьких значениях деформации, закон Гука для сдвига принимает вид:

(209)

26.2Деформация кручения.

Деформации кручения возникают при закручивании одного основания образца

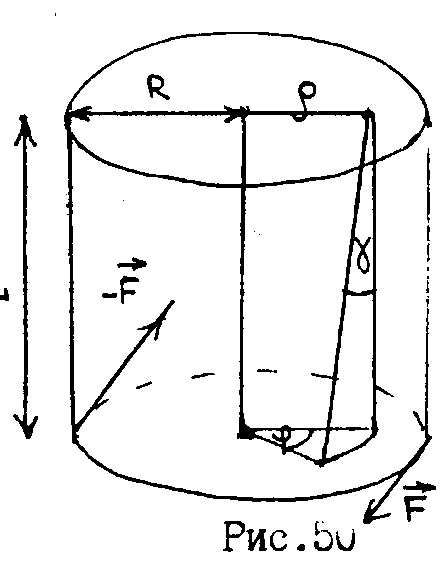
относительно другого .

По закону Гука для этого типа деформации:

(210)

где - угол закручивания, - длинна образца, - момент закручивающих сил, 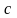- коэффициент кручения.

Величина называется модулем кручения т. е.

(211)

Одновременно с закручиванием образца происходит сдвиг его слоёв. Угол сдвига определяется из закона Гука.

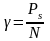(212)

Угол сдвига можно получить и из чисто геометрических соображений:

(213)

Сравнивая (212) и (213), получим

(214)

Момент распределённых сил, приложенных к нижнему основанию образца, получим, используя (214)

Рис.51

Из рис.51 видно, что элементарный момент закручивающих сил, приложенных к элементу основания, равен:

(215)

Полный момент:

(216)

Сравнивая (210) и (216), получаем связь между модулями сдвига и кручения:

27. Закон всемирного тяготения.

Закон всемирного тяготения получен Ньютоном из наблюдений видимого движения планет Солнечной системы, используя законы динамики. В векторной форме закон всемирного тяготения, определяющий силы гравитационного взаимодействия, имеет вид:

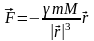(218)

где - масса источника гравитационного поля, - величина пробной массы, 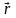-радиус-вектор точечной пробной массы относительно центра масс источника поля, - гравитационная постоянная.

Силовой характер поля источника является сила, действующая на единичную пробную массу, помещённую в данную точку поля. Эта величина называется напряжённостью поля:

(219)

Следует отметить, что закон всемирного тяготения справедлив только для точечных взаимодействующих масс. Кроме того, массы тел, фигурирующие в законе всемирного тяготения, имею другой смысл, нежели в законах динамики. Это –“тяготеющие”,”тяжёлые” или ”гравитационные” массы.