23.2. Силы трения качения.

Трение качения возникает при качении одного твердого тела по поверхности другого. При попытке сдвинуть тело по поверхности другого в плоскости соприкосновения возникает

с ила препятствующая этому (рис. 43).

Положим, что оба тела являются абсолютно твердыми, недеформируемыми, В этом случае нормальная составляющая реакции проходит через точку касания и центр масс катка (считаем его однородным симметричным телом, например, цилиндром). При такой модели любая по величине сила может вызвать качение катка, т.е. сопротивление движению.

не возникает. Более того, сила 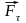должна вызывать угловое ускорение при любой по величине силе , что противоречит опыту.

Сопротивление качению может возникать в том случае, если нормальная реакция смещается относительно вертикального диаметра катка в сторону движения. Это происходит в том случае, если давление катка на поверхность будет не в точке, а по участку поверхности, а интенсивность давления будет больше впереди вертикального диаметра катка, как показано на рис. 44.

Рис.44

Следовательно, поверхность должна деформироваться, причем деформации будут несимметричными относительно вертикального диаметра.

Положим, что сила вызывает равномерное качение катка, т.е.

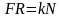
Откуда

(190)

Здесь 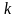(коэффициент трения качения) является размерной величиной. Смысл его- ''плечо'' нормальной составляющей реакции поверхности.

24. 1Вязкое трение

Вязкое трение возникает при относительном движении слоёв жидкости или газа. Основные законы вязкого трения получены опытным путём.

Ньютон установил, что если под действием силы площадка площади движется равномерно со скоростью относительно площадки (рис.45),

Рис.45

На подвижную площадку действуют силы сопротивления движению (силы вязкого трения):

где - расстояние между площадками (слоями), - коэффициент вязкого трения определяемая свойствами вязкой среды, заполняющей промежуток между площадками.

При движении тел в вязкой среде на них действуют силы сопротивления движению.

Стокс получил выражение для этих сил. При малых скоростях.

(192)

где: - стоксова сила сопративления, - плотность среды, - скорость тела, 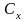-коэффициент, определяемый геометрией тела, - площадь проекции тела на плоскость, перпендикулярную направлению движения.

24.2 Движение тел в сопротивляющейся среде.

При достаточно больших скоростях тел (или если форма тела является плохо обтекаемой) силы Стокса становятся пропорциональны квадрату скорсти:

Положим, что тело начинает падать под действием силы тяжести в сопротивляющейся среде. Пренебрегая силой Архимеда, запишем:

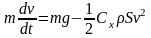
С течением времени скорость тела возрастает, возрастает и сила Стокса. Наконец, силы тяжести и Стокса уравновешиваются, после чего начинается равномерное движение тела с установившейся скоростью . Определим зависимость скорости от проходимого телом пути и значение установившейся скорости. Для этого сначала преобразуем (194):

Обозначим:

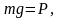
Тогда: Или:

Интегрируя (195), получим:

Константу интегрирования находим из начальных условий (x=0 и =0):

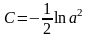
Подставив (197) в (196) получим

Или:

Откуда:

Через достаточно большой промежуток времени ( ) скорость тела перестаёт изменяться. Следовательно, значение установившейся скорости равно

(178) и (179) и дают искомое решение поставленной задачи.