VI. Лабораторные работы.

1. Изучение поступательного движения на машине атвуда

Цель работы: изучить закономерности поступательного движения твердого тела, освоить графический метод определения ускорения и момента силы трения; определить ускорение тела и величину момента силы трения.

Оборудование:

1. машина Атвуда;

2. грузы, связанные нитью;

3. комплект перегрузов;

4. секундомер.

Теоретическая подготовка:по учебникам [1-5] или по конспекту необходимо изучить темы «Кинематика и динамика материальной точки», «Динамика вращательного движения твердого тела». Особое внимание обратить на кинематическое уравнение равноускоренного движения, а также на законы динамики вращательного движения и определение моментов сил.

Сущность лабораторной работы и методика эксперимента.

Описание лабораторной установки:

Машина Атвуда (рис.1.1) состоит из вертикальной стойки с нанесенной на ней шкалой. В верхней части стойки закреплен легкий блок 4 известной массы, вращающийся с небольшим трением. Через блок перекинута легкая нить 3 с грузами 1 и 2 одинаковой массы m. К стойке крепится подвижная платформа 6, с помощью которой регулируется путь, пройденный грузами. К машине Атвуда придан комплект перегрузов, помещая которые на один из грузов, получают равноускоренное движение системы тел, состоящей из двух одинаковых грузов m, перегрузка m₁, и блока.

Часть I. Определение ускорения движения грузов.

При равноускоренном движении путь S, пройденный за время t определяется выражением:

Т.к. начальная скорость движения грузов , то

(1.1)

Если построить график зависимости S от (t²), то получим прямую, в которой будет являться угловым коэффициентом прямой.

Для построения графика определяем время прохождения грузом различных отрезков пути. Определив по графику tga - тангенс угла наклона прямой по отношению к оси абсцисс (t²), находим a= 2tg (см. рис. 1.2).

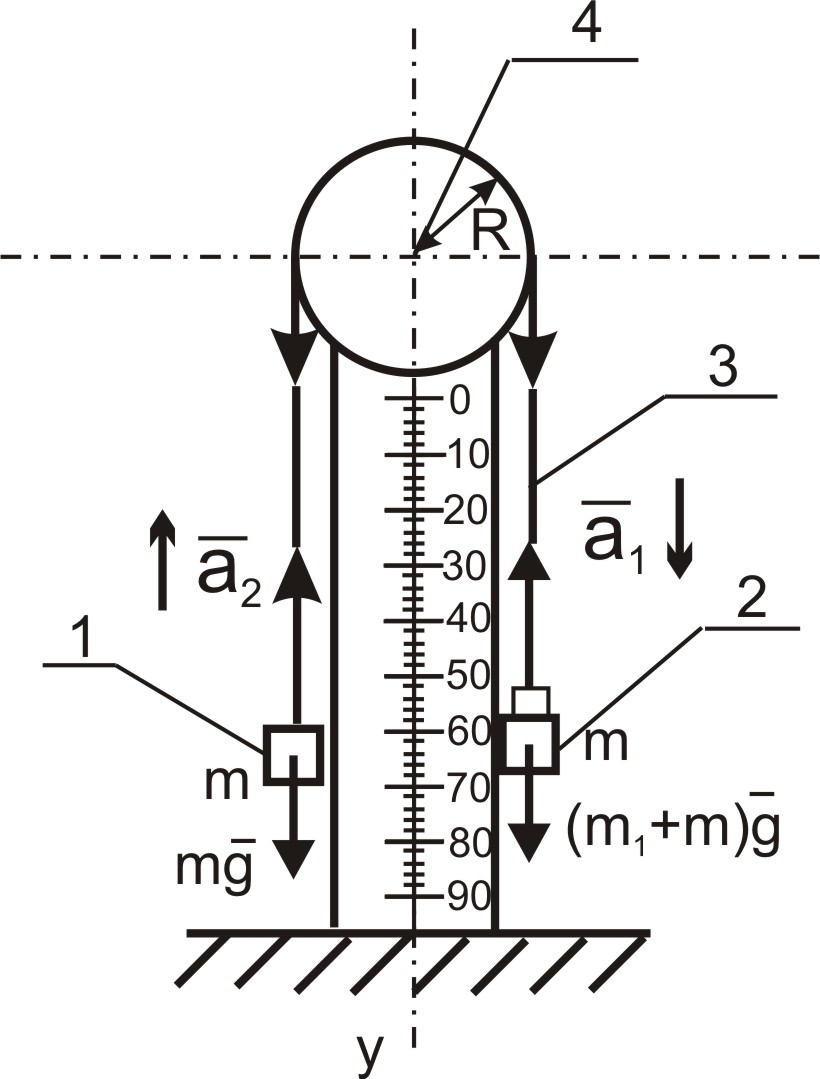
Рисунок 1.1

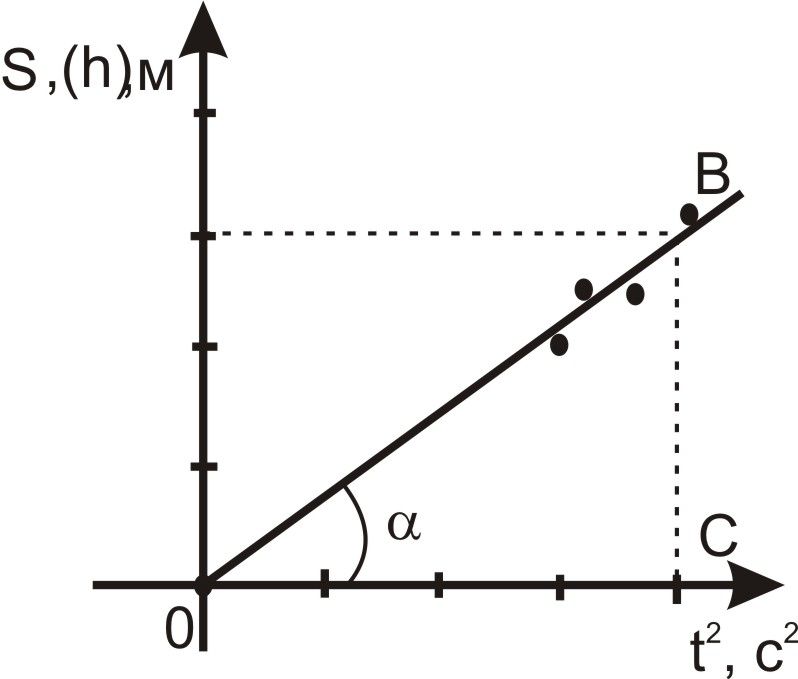
Рисунок 1.2.

Часть II. Определение момента трения в блоке.

Момент трения в оси блока можно определить, зная массу перегрузка m₁, который страгивает блок с грузами. Рассмотрим движение блока и грузов (см. рис. 1.1). Запишем уравнения движения грузов и блока. Для груза с перегрузом в соответствии со вторым законом Ньютона:

Для груза без перегрузка:

В проекциях на ось ОY получим:

Если считать нить не растяжимой, то , кроме этого, рассматривая движения нити и блока, можно записать

,

где e - угловое ускорение блока, R - радиус блока

Уравнение вращательного движения блока:

Так как масса нити мала по сравнению с массами грузов и блока, то и . Таким образом получаем систему уравнений:

;

,

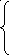из которой следует:

(1.2)

Очевидно, что ускорение зависит от массы перегрузка _1. При некотором ее значении ускорение будет равно нулю. Т.е. система будет неподвижна по причине действия момента силы трения. Из формулы (1.2) видно, что если , то М_тр=.

Необходимое значение находят по графику , (см. рис.1.3). График строят по четырем точкам.

Рисунок 1.3.

Порядок выполнения лабораторной работы: