3 Нормальний розподіл і основні розподіли, пов'язані з ним

1. Нормальний розподіл

Більшість імовірнісних методів базується на тому, що варіювання ознак підлягає визначеному закону розподілу. Ознаки об'єктів природного походження найчастіше розподілені нормально, тобто підлягають нормальному закону розподілу («закону Гаусса»). Головна особливість закону Гаусса полягає в тому, що він є граничним законом, до якого наближаються за певних умов інші закони розподілу. Нормальний закон найбільш часто зустрічається на практиці.

Для нормального закону розподілу щільність розподілу має вигляд

,

де m – математичне сподівання;

σ – середнє квадратичне відхилення ( – дисперсія).

Скорочено записують N (m, ).

Як впливає зміна параметрів m та σ на форму кривої Гаусса? Очевидно, що зміна m не змінює форму нормальної кривої (графіки функції f(x) і f(x -m ) мають однакову форму; графік f(x - m) будують шляхом зсуву графіка функції f(x) на m одиниць праворуч, якщо m > 0, і ліворуч, якщо m < 0).

Зі зміною σ максимальна ордината точки кривої змінюється. Оскільки площа, обмежена кривою розподілу, дорівнює одиниці при будь-якому значенні σ, то із зростанням σ крива Гаусса стає більш пологою, розтягується уздовж осі Ох .

На рис. 3.1 зображені нормальні криві при різних значеннях σ (σ₁ < σ < σ₂) і деякому значенні m (однаковому для всіх трьох кривих).

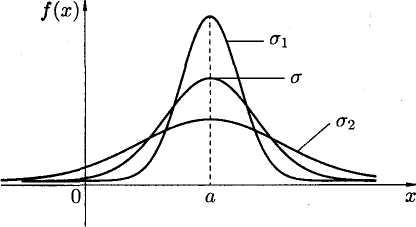
Рисунок 3.1 – Нормальні криві при різних значеннях σ (σ₁ < σ < σ₂).

Нормальному закону підлягають помилки вимірювань, величини зношування деталей у механізмах, ріст людини, помилки пострілів, вага бульб картоплі, величина шуму в радіо-прийомному пристрої, коливання курсу акцій та ін.

Стандартним нормальним розподілом називається розподіл з m=0 і σ =1: ,

– функція розподілу,

де –функція Лапласа. Це таблична функція, її значення протабульовані.

Введемо в розгляд - стандартний нормальний розподіл.

.

Тоді ймовірність попадання випадкової величини X ~ N(m, σ) на заданий проміжок (x₁,x₂) буде дорівнювати

.

3.1.1 Обчислення ймовірності заданого відхилення від математичного сподівання

Часто потрібно обчислити ймовірність того, що відхилення нормально розподіленої випадкової величини Х від математичного сподівання m за абсолютною величиною менше заданого , тобто .

, ,

,

.

Ймовірність того, що випадкова величина X набере значення, що відхиляється від математичного сподівання не більш ніж на задане (), більша в тієї величини, у якої менше. На рис. 3.2 наведено графік для випадку, якщо m = 0, σ₁<σ₂.

Рисунок 3.2 – Графік для випадку, якщо m = 0, σ₁<σ₂

3.1.2 Правило трьох сигм (3σ)

Ймовірність того, що випадкова величина X набере значення, що відхиляється від математичного сподівання не більше ніж на задане (), дорівнює

.

Нехай , тоді

.

Якщо , тоді .

.

Якщо випадкова величина розподілена нормально, то абсолютна величина відхилення від математичного сподівання не перевищує значення 3σ.

На практиці: якщо розподіл випадкової величини невідомий, але правило 3σ виконується, то є підстави припускати, що досліджувана випадкова величина розподілена нормально.

На нормальному законі розподілу базується практично вся параметрична статистика. Це пов'язано з тим, що більшість розподілів, що використовуються для перевірки статистичних гіпотез (Фішера, Стьюдента та ін.), є перетвореннями нормального закону розподілу.

Головна особливість нормального закону полягає в тому, що він є граничним законом, до якого прагнуть (при виконанні деяких вимог) всі інші закони розподілу.

В Excel існує 5 функцій, пов'язаних з обчисленням нормального розподілу.

НОРМСТРАСПР(x) – повертає значення ймовірності стандартного нормального розподілу для x.

НОРМСТОБР (ймовірність) – повертає значення x для стандартного нормального розподілу для заданої ймовірності.

НОРМРАСП(x, математичне сподівання, середнє квадратичне відхилення, ознака) – повертає значення функції щільності розподілу, якщо ознака =0, повертає значення функції розподілу, якщо ознака =1.

НОРМОБР(ймовірність, математичне сподівання, середнє квадратичне відхилення) – повертає значення x функції розподілу.

НОРМАЛИЗАЦИЯ(x, математичне сподівання, середнє квадратичне відхилення) – повертає нормоване значення x.