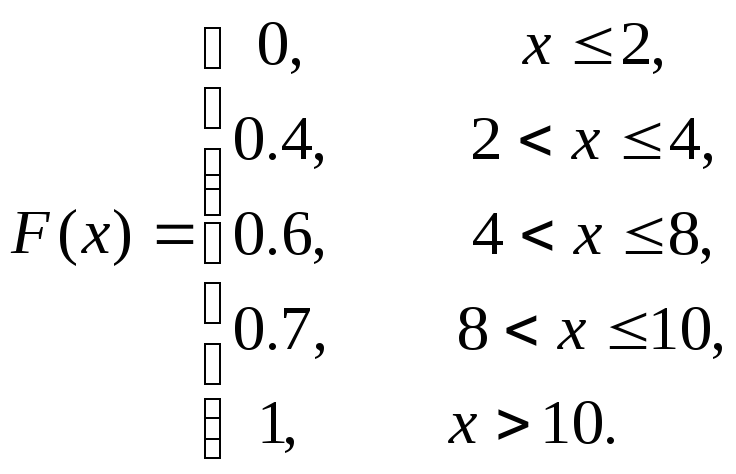- •1 Предмет курсу. Основні задачі
- •1.1 Математична модель. Види моделей
- •1.2 Типи розв'язуваних задач
- •3 Виявлення закономірностей (досліджуємо залежність одних змінних від інших):
- •4 Класифікація, тобто одержання відповіді на одне з питань:
- •1.3 Шкали вимірювання
- •1.4 Види шкал
- •1.5 Зв'язок шкал вимірювань і застосовуваних методів
- •Питання і завдання до розділу 1
- •2 Випадкові величини
- •2.1 Закон розподілу
- •2.1.1 Закон розподілу дискретної випадкової величини
- •2.1.2 Закон розподілу неперервної випадкової величини
- •2.2. Числові характеристики випадкових величин
- •2.2.1 Математичне сподівання
- •2.2.2 Дисперсія випадкової величини
- •2.2.3 Середнє квадратичне відхилення випадкових величин
- •2.2.4 Мода і медіана
- •Графік функції розподілу
- •Питання і завдання до розділу 2
- •Лабораторна робота Тема. Основні характеристики дискретної випадкової величини.
- •3 Нормальний розподіл і основні розподіли, пов'язані з ним
- •Нормальний розподіл
- •3.1.1 Обчислення ймовірності заданого відхилення від математичного сподівання
- •3.1.2 Правило трьох сигм (3σ)
- •3.1.3 Моменти
- •3.1.4 Оцінка відхилення теоретичного розподілу від нормального. Асиметрія та ексцес
- •3.2 Розподіл χ2 (розподіл Пірсона)
- •Функції Excel
- •3.3 Розподіл Стьюдента (t – розподіл)
- •Питання і завдання до розділу 3
- •Лабораторна робота Тема. Нормальний закон розподілу
- •4 Вибірковий метод
- •4.1 Теорема Чебишева
- •4.2 Основні поняття вибіркового методу
- •4.3 Емпіричний закон розподілу
- •4.3.1 Статистичний розподіл у вигляді таблиці
- •4.3.2 Графічне зображення статистичного розподілу
- •4.3.3 Побудова гістограми
- •4.4 Статистичні оцінки параметрів розподілу
- •4.4.1 Міри положення
- •4.4.2 Міри розсіювання
- •4.4.3 Міри форми
- •4.5 Визначення параметрів з використанням ms Excel
- •4.6 Довірчий інтервал
- •4.6.1 Довірчий інтервал для оцінки математичного сподівання нормального розподілу при невідомому
- •4.6.2 Довірчий інтервал для середнього квадратичного відхилення (нормальний розподіл)
- •Питання і завдання до розділу 4
- •Лабораторна робота Тема. Обчислення основних статистичних характеристик вибірки
- •5 Статистична перевірка статистичних гіпотез
- •Помилки першого і другого роду
- •5.1 Перевірка гіпотези про закон розподілу
- •5.1.1 Емпіричні та теоретичні частоти. Безперервний розподіл
- •5.1.2 Критерій згоди Пірсона
- •5.2 Поняття про параметричну, непараметричну і робастну статистику
- •5.3 Порівняння двох дисперсій нормальної генеральної сукупності
- •5.3.1 Критерій Фішера
- •5.4 Порівняння виправленої вибіркової дисперсії з гіпотетичною генеральною дисперсією
- •5.5 Перевірка гіпотез про середні для нормальної генеральної сукупності
- •5.5.2 Перевірка гіпотези про рівність середніх при нерівних дисперсіях (малі вибірки)
- •5.5.4 Перевірка гіпотези про рівність середніх при зв'язаних вибірках
- •5.5.5 Порівняння вибіркової середньої (з генеральної нормальної сукупності) із заданим а
- •Питання і завдання до розділу 5
- •6 Перевірка наявності зв'язку між змінними
- •6.1 Кореляційний аналіз (ка)
- •6.1.1 Властивості коефіцієнта кореляції
- •Зауваження
- •6.1.2 Значущість коефіцієнта кореляції
- •6.2 Поняття про багатовимірний кореляційний аналіз
- •6.2.1 Часткова кореляція
- •6.2.2 Множинний коефіцієнт кореляції
- •Питання і завдання до розділу 6
- •Лабораторна робота Тема. Багатофакторний кореляційний аналіз
2.2.2 Дисперсія випадкової величини
Дисперсія випадкової величини визначається як математичне сподівання квадрата відхилення випадкової величини від її математичного сподівання:
![]() ,
,
![]() - для дискретної випадкової
величини Х,
- для дискретної випадкової
величини Х,
![]() - для неперервної випадкової
величини Х.
- для неперервної випадкової
величини Х.
Дисперсія звичайно розраховується за формулою
![]() .
.
![]() для дискретної
випадкової величини Х,
для дискретної
випадкової величини Х,
![]() ,
для неперервної
випадкової величини Х.
,
для неперервної
випадкової величини Х.
Дисперсія дозволяє оцінити розсіювання можливих значень випадкової величини відносно її середнього значення.
Властивості:
1 Дисперсія постійної дорівнює нулю
D(С) = 0.
2 Постійний множник можна виносити за знак дисперсії, звівши його у квадрат
D(СХ) = С2D(X).
3 Дисперсія суми незалежних випадкових величин дорівнює сумі їх дисперсій
D(X+Y)=D(X)+D(Y).
4 Дисперсія випадкових величин не зміниться, якщо до цієї випадкової величини додати постійну
D(X + С)= D(X).
5 Якщо випадкові величини X і Y незалежні:
D(XY) = MX2 · MY2 - (МХ)2·(МY)2.
2.2.3 Середнє квадратичне відхилення випадкових величин
Дисперсія D(X) має розмірність квадрата випадкової величини X, що є незручним при порівнянні. Коли бажано, щоб оцінка розкиду (розсіювання) мала розмірність випадкової величини, використовують ще одну числову характеристику – середнє квадратичне відхилення.
Середнім квадратичним відхиленням або стандартним відхиленням випадкової величини X називається квадратний корінь із її дисперсії, позначають його через σ(Х) (або σХ). Таким чином, за визначенням
![]() .
.
2.2.4 Мода і медіана
Модою дискретної випадкової величини X називається її значення, набуте з найбільшою ймовірністю в порівнянні з двома сусідніми значеннями, позначається через М0 (Х). Для неперервної випадкової величини M0 (X) - точка максимуму (локального) щільності f(x).
Якщо мода єдина, то розподіл випадкової величини називається унімодальним, у протилежному разі – полімодальним.
Медіаною Ме (Х) неперервної випадкової величини X називається таке її значення хр, для якого
![]()
тобто однаково ймовірно, що випадкова величина X виявиться менше хр або більше хр .
Для дискретної випадкової величини X медіана звичайно не визначається.
 x
x
М0 (Х) хр=Ме (Х) М0 (Х)
Рисунок 2.6 – Мода та медіана для неперервної випадкової величини
Приклад. Дано закон розподілу дискретної випадкової величини Х.
|
Х |
2 |
4 |
8 |
10 |
|
Р |
0,4 |
0,2 |
0,1 |
0,3 |
Побудувати многокутник розподілу, визначити функцію розподілу, математичне сподівання, дисперсію, середнє квадратичне відхилення. Побудувати графік функції розподілу.
Многокутник розподілу

Функція розподілу:
|
Х |
2 |
4 |
8 |
10 |
|
Р |
0,4 |
0,2 |
0,1 |
0,3 |
|
F(x) |
0,4 |
0,6 |
0,7 |
1 |
Аналітичний вигляд функції розподілу: