Уравнение равновесия системы сил, произвольно расположенных на плоскости.

Пара сил – две равные параллельные и противоположно направленные силы.

Момент пары сил – момент, равный произведению одной из этих сил на плечо.

Две пары сил эквивалентны в том случае, если после замены одной пары сил другой, механическое состояние тела не изменится. При этом, изменив величину силы и плеча новой пары необходимо сохранить равенство их моментов. (рис 4). М₁ эквивалентна М_{2 .}

В случае когда в системе пар сил момент результирующей пары равен нулю то можно считать что система находится в равновесии.

Момент силы относительно точки равен произведению модуля силы на длину перпендикуляра, опущенного из этой точки на прямую действия силы (рис.4).

М_А=Р*h

Лемма Пуассо

Действие силы на твердое тело не изменится, если эту силу перенести параллельно своему первоначальному направлению в любую точку , и приложить при этом пару сил с моментом равным произведению силы на расстояние от точки приведения до первоначального положения исходной силы. (рис 6) М= Р*ОК

Б43: Реакции связи и методы их определения.

Статика Понятия и определения

Статика – наука, изучающая равновесие системы сил, действующих на тело.

Различают нагрузки:

Сосредоточенные (когда площадь действия нагрузки стремится к нулю) [Н];

Распределенные (нагрузка может быть распределена: а) по длине [Н/м], б) по площади [Н/м²], в) по объему [Н/м³];

Статические нагрузки, плавно изменяющиеся от нуля до определенной величины;

Динамические (нагрузки, связанные с действием ускорения, могут быть повторно-переменными);

Ударные (нагрузки, с высокими значениями ускорений ).

Аксиомы статики

1. Свободное и абсолютно твердое тело находится в равновесии под действием двух сил тогда, и только тогда, когда действующие на него силы противоположно направлены, действуют по одной прямой и имеют равные модули.

2. Действие данной системы сил на данное тело не изменится, если к нему присоединить (или отнять) систему сил, равнодействующая которой равна нулю.

3. Две силы, приложенные к точке, эквивалентны равнодействующей силе, приложенной к этой точке, определяемой по правилу параллелограмма.

4. Равновесие тела сохранится, если наложенные на него связи заменить реакциями связи.

Связи – материальные тела, ограничивающие перемещение тела. Сила, с которой связь действует на тело, называется реакцией связи.

Связи и реакции связи

В пространстве возможно шесть перемещений (рис. 1) 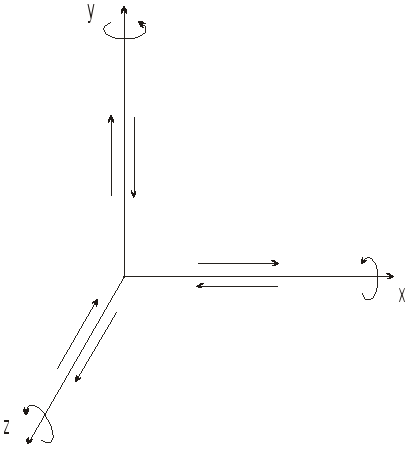, а на плоскости – три (рис.2) .

Реакции связи всегда противоположны тому направлению, по которому связь препятствует движению.

Реакция связи – сила, с которой связь препятствует перемещению.

Примеры реакции связи:

Обозначения:

G – внешняя нагрузка,

N – нормальная составляющая реакции R,

T – касательная составляющая реакции R,

V – вертикальная составляющая реакции R,

H – горизонтальная составляющая реакции R.

Пример поверхности без трения (рис.1) . Реакция связи направлена по нормали к опорной поверхности.

Поверхность с трением (рис.2)

.Полная реакция связи равна геометрической сумме нормальной и касательной составляющих этой реа

Реакция, действующая вдоль гибкой связи (рис.3) , работает на растяжение.

Реакция неподвижного цилиндрического шарнира (рис.4, точка А) лежит в плоскости перпендикулярной его оси, имеет радиальное направление и определяется как:

У шарнирно подвижной опоры (рис.4, точка В) горизонтальной со­ставляющей реакции опоры не будет, т.к. горизонтальная сила компенсиру­ется перемещением вдоль горизонтальной поверхности. Консольная опора (жесткая заделка).

В общем случае будет вертикальная V_A, горизонтальная Н_А состав­ляющие реакции R_A и реактивный момент М_А.

Б46: Основы кинетостатики. Принцип Даламбера.

Основы кинетостатики

Принцип Даламбера

Пусть материальная точка М совершает движение с ускорением. На эту точку действует сила и равнодействующая сил реакции связи R. Добавим силу инерции точки М - Ф.

F=.

Для данной системы запишем условие равновесия, с учетом силы инерции.

Тогда сила инерции определится как:

Принцип: Если к действующим на точку активным силам и реакциям добавить силу инерции, то в каждый момент времени полученная система сил будет уравновешена.

Принцип Даламбера представляет собой формальный математический прием, удобный для решения задач динамики. Этот прием позволяет записывать динамические уравнения движения в форме уравнений равновесия.

Особенности:

При криволинейном движении:

Для системы внешних и внутренних сил, принцип Даламбера может быть представлен в следующем виде:

(1)

где - сумма внешних сил, - сумма внутренних сил, - сумма сил инерции.

Принцип Даламбера может быть записан и для моментов сил:

. (2)

В механике макрообъектов внутренние силы считаются уравновешенными, и с учетом этого можем считать:

Можно принять, что силы и моменты инерции, представляются главным вектором и главным моментом сил инерции:

В проекциях на оси координат получают уравнения, аналогичные уравнениям статики:

Для пространственной системы:

Для плоской системы:

Расчеты при динамических нагрузках.

Если известны действующие силы и силы инерции, возможно использование метода сечений и уравнения равновесия.

Силы инерции вызывают в элементах конструкции дополнительные нагрузки и соответствующие напряжения. Для простоты эти напряжения можно считать статическими, но вызванными силами инерции.

Для решения задач прочности связанными с динамическими нагрузками:

1. Определение ускорения точек;

2. Определение сил инерции;

3. Элемент (конструкция) нагружается силами инерции и внешними силами;

4. Расчеты ведутся по аналогии с расчетом статических систем.

Пример: Требуется определить напряжение в тросе на расстоянии z от его конца. (Рис. 1).

уравнение равновесия

Определение массы поднимаемой системы

Определение силы инерции

Определяем усилия, действующие на тросс

- объемный вес материала троса, А – площадь поперечного сечения троса.

Допускаемое напряжение с учетом зависимости (1) может быть представлено в следующем виде:

Б47: Червячные передачи. Усилия в зацеплении. Основы расчета на прочность.

Червячные передачи.

Червячная передача относится к числу так называемых зубча­то-винтовых, т. е. имеющих признаки, характерные и для зубча­тых, и для винтовых передач.

Основные достоинства червячной передачи, обусловившие ее широкое распространение в различных отраслях машиностроения:

1. Плавность и бесшумность работы;

2. Возможность получения больших передаточных чисел при сравнительно небольших габаритах передачи. Червячные пере­дачи применяются с передаточными числами от u = 5 до u = 500. Диапазон передаточных чисел, применяемых в силовых передачах, u = 10-80 (в редких случаях до 120).

3. Компактность.

Недостатки червячной передачи:

1. Сравнительно невысокий к. п. д.

2. Сильный нагрев передачи вследствие перехода потерь на трение в тепловую энергию. Для уменьшения нагрева в червячной передаче применяют масляные резервуары с ребристыми стенками с целью более интенсивной теплоотдачи в окружающий воздух, обдув корпуса и другие способы охлаждения.

3. Небольшие передаваемые мощности.

Червячные передачи различают по числу заходов червяка — одно-, двух-, трех- и многозаходные; по расположению вала чер­вяка — относительно червячного колеса с верхним, нижним и боковым расположениями.

Усилия, действующие в зацеплении

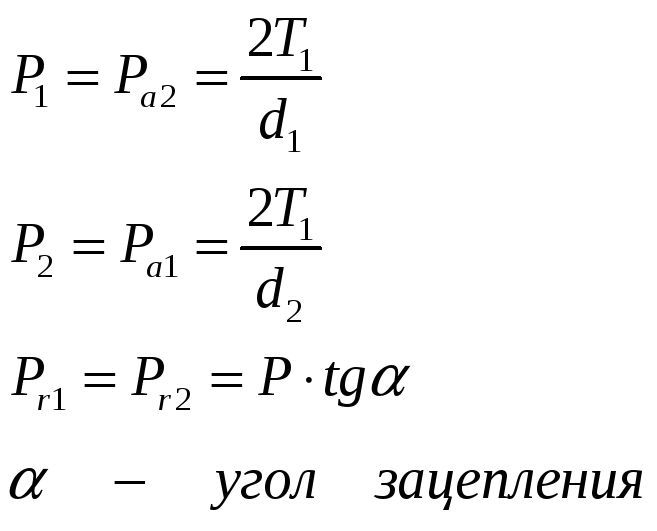
d₁,d₂ – делительные диаметры червяка и колеса соответственно.

Особенности расчета червячных передач

Проектный расчет на контактную прочность строится на основе определения межосевого расстояния

Проверочный расчет на изгиб

1,2 – коэффициент упрочнения зуба за счет его длины и дугообразности.

у – коэффициент формы зуба.

Б48: Кинематический анализ рычажных механизмов.

Рычажные механизмы

Кинематический анализ рычажных механизмов предусматривает определение положения звеньев и построение траектории движения отдельных точек механизма. Определение линейных скоростей точек и угловых скоростей звеньев механизма, ускорений точек и угловых ускорений звеньев механизма.

1. Определение положения звеньев.

Рис. 1

Используя начальные условия определяем положение точки С

2. Определение скоростей.

Дифференцируя любой угол по , получаем безразмерную скорость /или ее аналог/. Связь между действительной угловой скоростью и ее аналогом можно записать в следующем виде:

Аналогично и для линейной скорости:

Дифференцируя по систему (1) и умножая на угловую скорость 1 звена, получим систему 2:

Первое уравнение из системы (2) определяет линейную скорость точки С, а из второго уравнения можно определить угловую скорость второго звена:

Вводя аналог ускорения аналогичным образом определяется ускорение точки С и угловое ускорение второго звена:

В системе 2 переменными являются не только φ₂, но и w₂

Из второго уравнения третьей системы можно найти угловое уравнение третьего звена .

Б50: Главный вектор и главный момент. Приведение системы сил к простейшему виду.

Главный вектор и главный момент

Пусть к телу в точке А, В и С приложена плоская система сил (Р1,Р2,Р3) (Рис 7) при параллельном переносе этих сил в точку О получается новая плоская система сил (Р1’,Р2’,Р3’) а также система пар сил Р₁ Р’’₁ ; Р₂ Р’’₂ ; Р₃ Р’’₃ ; эти пары сил можно определить в следующих зависимостях М (Р₁)= Р₁*а, М (Р₂)= Р₂*b, М (Р₃)= Р₃*c.

Главный вектор новой системы сил равен геометрической сумме векторов системы приведенных с к точке 0.

Главный момент системы относительно заданной точки О, равен сумме моментов сил, относительно той же точки.

Произвольная плоская система сил (Р1,Р2,Р3) эквивалентна силе приложенной в точке О и равна главному вектору , а так же паре сил с моментом (главный момент системы).

Приведение плоской системы к простому виду.

1. Выбрать систему координат

2. Выбрать центр приведения

3. Вычислить проекции главного вектора на координатные оси (V_x ,V_y)

4. Вычислить модуль главного вектора

5. Вычислить главный момент.

Возможны следующие виды при приведении к простому виду

1. V и М₀ не равны 0, в этом случае равнодействующая равнаV который отстоит от равнодействующей на величину h где h= М₀ /V

2. V не равна 0, М₀ равна 0 система приводится к равнодействующей при этом R=V и совпадает с линией вектора

3. V равна 0, М₀ не равна 0 – система приводится к паре сил с иоиентом равному главному моменту

4. V =М₀ = 0 – в этом случае система находится в равновесии для уравнения равновесия сил произвольно расположенных на плоскости V и М₀ должны быть равны 0, в связи с этим реализуется несколько форм равновесия

а) б)