Основы динамики точки и тела. Динамика механизмов.

1. Понятия и определения.

Основными задачами динамики являются:

1. По известному закону движения определить действующие силы.

2. Зная действующие силы и начальные условия, определить закон движения (тела, точки, механизма).

Аксиомы динамики

1. Всякая свободная от внешнего воздействия материальная точка сохраняет свое состояние покоя или равномерного движения, до тех пор, пока к этой точке или телу не будет приложена сила.

2. Модуль силы, действующей на материальную точку, равен произведению массы этой точки, на модуль ускорения. Направление действия силы, совпадает с направлением ускорения.

3. Две материальные точки действуют друг на друга с силами равными по модулю и противоположными по направлению, вдоль прямой, соединяющей их центры.

4. Если на материальную точку действует одновременно несколько сил, то каждая из них сообщает точке ускорение, модуль которого равен модулю этой силы, деленному на массу этой точки.

Тогда для системы сил, ускорение будет определяться суммой сил, деленных на массу этой точки:

.

Работа. Мощность. Кинетическая энергия.

На прямолинейном участке .

Для криволинейного участка , где α – угол между направлениями перемещения и силы.()

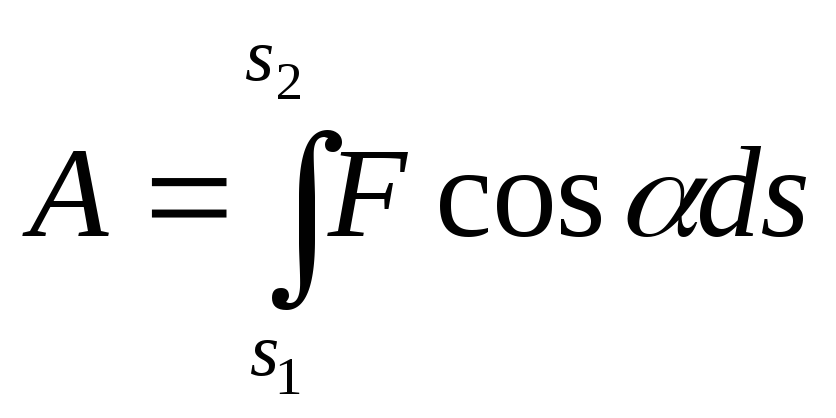
Выражение для работы по перемещению тела под действием силы, на конечном криволинейном участке, с учетом криволинейной траектории, в декартовой системе координат может быть записано следующим образом:

.

Выражение для мощности при поступательном движении имеет следующий вид:

, при вращательном движении , где Т_с – сила сопротивления.

Кинетическая энергия поступательного движения определится по формуле:

Если имеется система точек, то их общая энергия:

, где М – масса тела, состоящего из нескольких точек, а V_C – скорость центра масс.

Энергия системы точек при вращательном движении может быть определена по формуле:

w- угловая скорость точек относительно центра масс.

Т. К. то

Для различных тел различны моменты инерции.

Так для диска , а для кольца .

2.

Теорема об изменении кинетической энергии.

Изменение кинетической энергии материальной точки за некоторый промежуток времени равен работе, приложенных к этой точке сил, затраченной на перемещение этой точки за этот промежуток времени.

(1)

Проектируем вектор силы на вектор скорости:

(2)

Интегрируя последнее выражение в пределах от V₀ до V, получим:

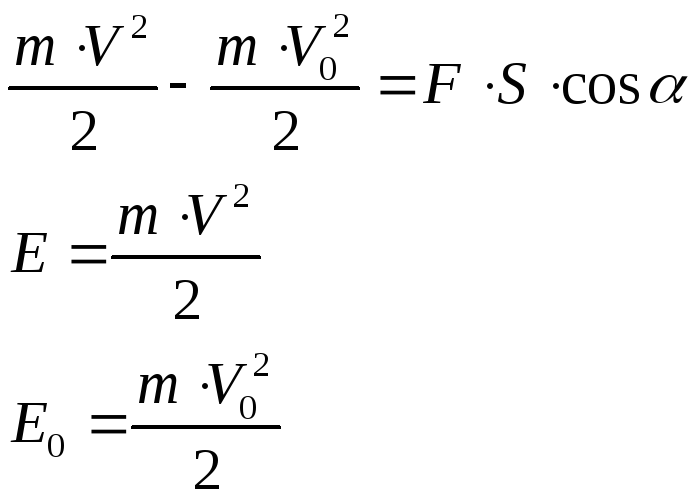Изменение кинетической энергии:

.

Теорема об изменении кинетической энергии показывает, что эффект действия силы, выражающийся в изменении кинетической энергии материальной точки, измеряется работой этой силы.

Для системы, состоящей из n точек, эта теорема может быть записана следующим образом:

.

Для системы точек вводится понятие центра масс. Так в декартовой системе координат, координаты центра масс можно записать в следующем виде:

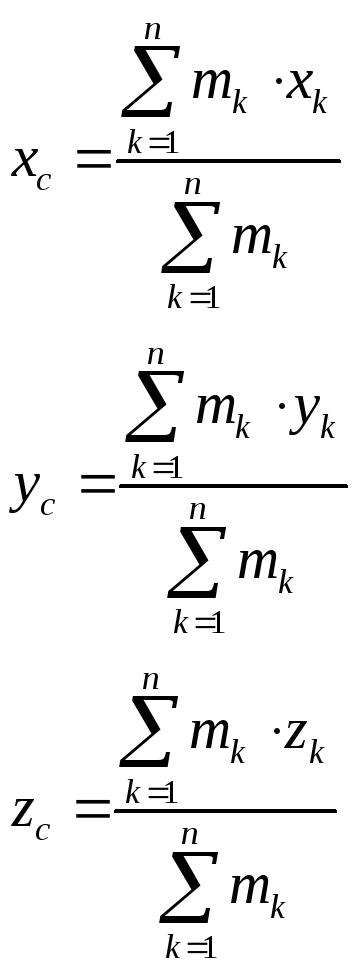
Цилиндрические косозубые и шевронные колеса.

Особенности геометрии.

Зубья прямозубого колеса входят в зацепление сразу по всей длине, вызывая удары из-за неточности изготовления.

При окружных скоростях V>6 м/с рекомендуется переходить на косозубые и шевронные колеса.

С – смещение зуба;

P_s – торцевой шаг;

P_n – нормальный шаг;

β – угол наклона зубьев (10˚…20˚);

b – ширина венца колеса;

b₁ – длина зуба.

Учитывая пропорциональность шага и модуля зацепления, торцевой модель будет определяться исходя из зависимости:

.При проектировании косозубых передач в качестве стандартного модуля выбирают нормальный модуль и угол зацепления в нормальном сечении равным 20˚.

В косозубых передачах с внешним зацеплением одно колесо делается с правым наклоном зуба, другое – с левым.

В передачах с внутренним зацеплением углы наклона зубьев совпадают по направлению.

d – начальный (делительный) диаметр.

z – количество зубьев.

.

Диаметр окружности выступов:

Диаметр окружности впадин:

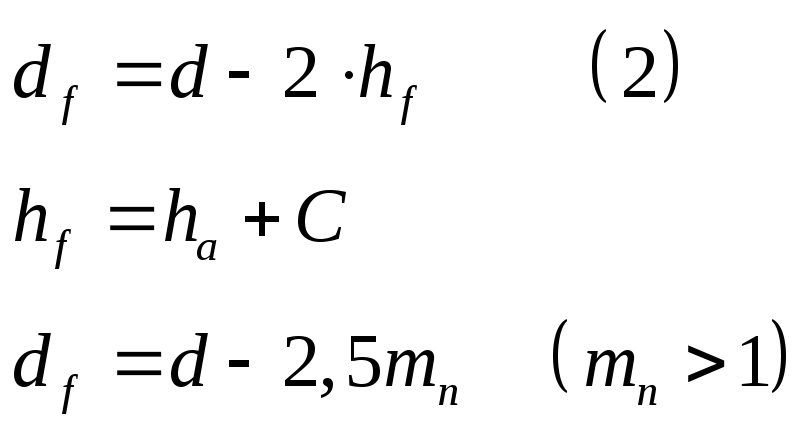
Под условием отсутствия подрезания принимаем минимальное количество зубьев:

- коэффициент торцевого перекрытия.

Усилия, действующие в зацеплении.

P_1A, Р_2A – осевые силы, возникающие из-за наклона зубьев, для их устранения применяют шевронные колеса со встречным наклоном зубьев.

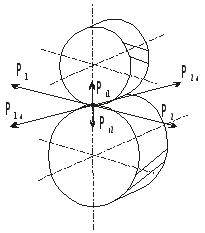
Для косозубых передач осевые усилия можно найти по формуле:

.

Формула для нахождения радиальных усилий имеет вид:

Где α – угол зацепления, β – угол наклона зуба.

В косозубых передачах появляется осевая составляющая сил зацепления

Для устранения осевых усилий применяют шевронные колеса.

Особенности расчета косозубых передач.

При расчете на контактную прочность косозубых передач используются основные зависимости для расчета прямозубых передач, с учетом снижения нагрузки на зуб, за счет увеличения длины зуба.

В качестве коэффициента снижения нагрузки используется коэффициент θ=1.15.

Тоже самое делают при расчете на изгиб.

По сравнению с прямозубыми цилиндрическими передачами у косозубых передач межосевое расстояние и модуль зацепления (при прочих равных условиях) несколько меньше.