Растяжение и сжатие.

Механические характеристики материалов

По механическим характеристикам материалы можно условно разделить на пластичные и хрупкие.

По механическим характеристикам материалов, к которым относятся: предельные напряжения, ударная вязкость, твердость и т.д., определяется работоспособность механических деталей машин и приборов.

Теоретически рассчитать механические свойства материалов затруднительно, поэтому эти свойства изучают экспериментально. Наиболее общий способ испытаний – растяжение и сжатие. При этом все материалы делятся на пластичные (например стали) и хрупкие (например чугун).

Эти испытания проводятся в специальных машинах и прессах.

Пластичные материалы могут деформироваться до 300% (фторопласт). Сталь может деформироваться без разрушения примерно на 5%.

Диаграмма в координатах называется машинной и зависит от размеров образца, поэтому ее заменяют условной диаграммой в координатах , в которой нет этой зависимости.

I – участок пропорциональности (участок, на котором выполняется закон Гука;

II – на отрезке АВ сохраняется упругость материала; на ВС появляются пластические (необратимые) деформации;

на СD – реализуется текучесть материала, которая характеризуется тем, что деформация изменяется, практически вне зависимости от нагрузки;

III – участок упрочнения материала: происходит уплотнение структуры (для пластмасс реализуется ориентация макромолекул);

IV – участок накопления повреждений, который заканчивается разрушением образца.

Используя диаграмму растяжений, рассмотрим предельные характеристики материалов:

- предел пропорциональности;

- предел упругости в точке В;

- предел текучести;

- предел временного сопротивления в точке М.

Для хрупких материалов практически не реализуется закон Гука, и вид диаграммы может быть следующим.

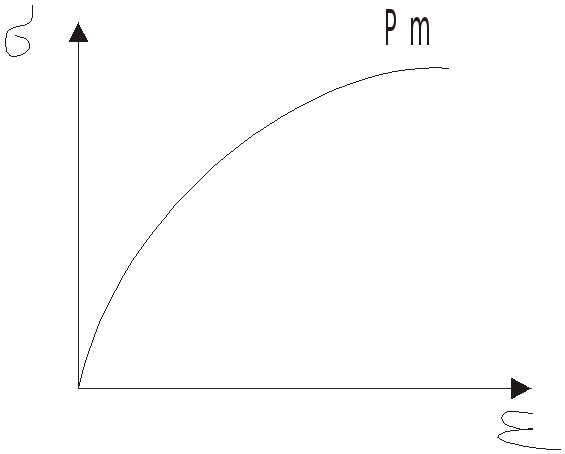
На этой диаграмме выделяют условный предел текучести, который определяют, как 0,2% от деформации образца.

Б6: Напряжения и перемещения при растяжении и сжатии. Закон Гука.

Растяжение и сжатие.

Напряжение и перемещение.

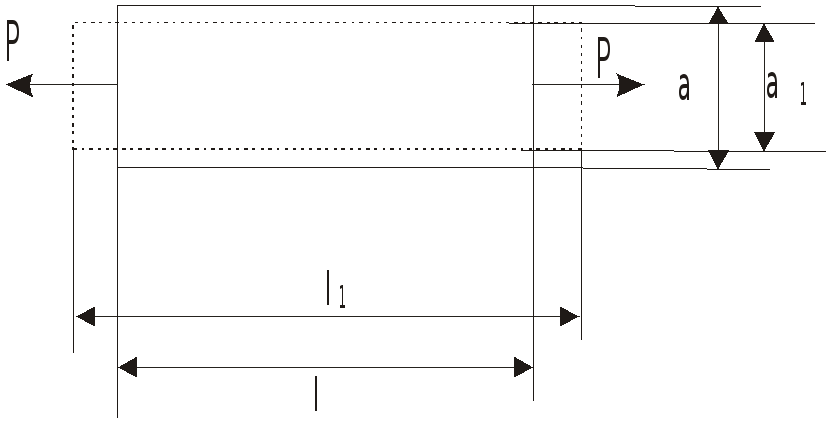
Р – продольная сила;

l – продольный размер бруса;

а – поперечный размер бруса;

- абсолютное удлинение;

- абсолютное сужение бруса.

(1) - относительная продольная деформация (удлинение);

- относительная поперечная деформация;

Для большинства материалов влияние одной деформации на другую ограничено.

Коэффициент Пуассона показывает взаимное влияние продольной и поперечной деформации друг на друга. При этом для большинства материалов .

В случае растяжения, из имеющейся зависимости, можно записать, при А=const, (2).

Экспериментально установлено, что при малых деформациях для большинства твердых тел имеет место прямая пропорциональность между нагрузкой и абсолютной деформацией.

- закон Гука (3)

Е – модуль упругости первого рода (модуль Юнга) характеризует упругие свойства материалов.

Если возьмем зависимости 1 и 2 и подставим в 3, то получим:

Другими словами, абсолютное удлинение прямо пропорционально внутренней силе действующей на отрезке равном l, и обратно пропорционально площади сечения этого бруса и упругим свойствам материала, из которого изготовлен брус.

Б7: Допускаемые напряжения и запасы прочности.

Допускаемые напряжения и запас прочности.

Допускаемые напряжения [] – это такие напряжения, при которых обеспечивается долговечность и прочность конструкции.

При расчетах элементов конструкции и машин механические характеристики материалов и нагрузок, как правило, отличаются от практических.

Многое факторы, действующие на конструкцию, носят случайный характер и не поддаются прогнозированию.

Механические свойства материалов, как правило, не стабильны. Учет всех факторов при расчетах вносит усложнения и неоправданные затраты труда и времени.

Для надежной работы элементов конструкции принимают коэффициент запаса прочности по отношению к экспериментально определенным механическим характеристикам материалов.

n – действительный коэффициент запаса прочности;

[n] – нормативный коэффициент запаса прочности.

Для пластичных материалов

Для хрупких материалов

Нормативный коэффициент запаса прочности определяется как произведение частных коэффициентов запаса прочности

[n]=[n1]*[n2]*…*[nk]

Частные коэффициенты запаса прочности учитывают неоднородность материала, точность расчетной схемы, степень ответственности детали и условия ее работы.

Для нормальной работы деталей машин, различных конструкций и приборов необходимо учитывать условия прочности, жесткости и устойчивости.

В данных условиях можно решать три типа задач на сопротивление материалов:

1. проверочная – когда сравниваются рабочие и допускаемые напряжения и перемещения, которые соответствуют условиям прочности 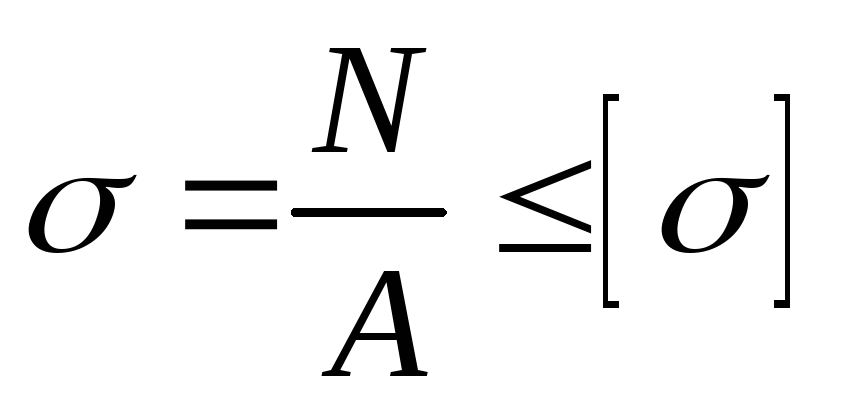и жесткости ;

2. проектная – в задаче определяются размеры конструкции;

3. Задача по определению несущей способности.

Б8: Расчеты на прочность и жесткость статически определимых и стат. неопределимых систем при растяжении и сжатии.

Решение задач на прочность и жесткость

Основой для решения статически определенных задач являются:

Метод сечений, уравнения равновесия, условия

прочности жесткости.

Дано:

Е=2*10⁵МПа

l_AB=l_ВС=l_CD=1м

Р=100кН

А₁=0,5*10³мм²

А₂=2А₁

[]=150 Н/мм²

Найти:N_i,_i,_i.

Определение внутренних сил:

Определение внутренних напряжений:

Условие прочности не выполняются, т.к. на участке ВС рабочее напряжение больше допускаемого.

Определение перемещений:

Особенности построения эпюр

1Скачки значений на эпюре внутренних сил определяются (или равны) внешними силами, приложенными в этой точке.

2Скачки эпюр на эпюре напряжений определяются изменением, как внешних сил, так и изменением размеров сечений.

3Эпюры напряжений, в данном случае, являются производной от эпюр перемещений.

Решение статически неопределимых задач

Если число неизвестных реакций связи оказывается больше числа уравнений равновесия, то такая система является статически неопределимой.

Разница между числом неизвестных реакций и числом уравнений равновесия определяет степень статической неопределенности системы.

При решении статически неопределимых задач составляются недостающие уравнения, которые учитывают совместные перемещения в данной системе.

С учетом известных перемещений предлагаются физические зависимости, например, в виде закона Гука, или в виде линейных температурных деформаций, для раскрытия сущности указанных совместных перемещений и, в дальнейшем, эти полученные уравнения решаются совместно.

Этапы раскрытия статической неопределенности (рассмотрим на примере решения задачи данные по размерам и нагрузкам смотри на предыдущей странице):

Статика – составление уравнений равновесия;

(Данная задача один раз статически неопределима)

Геометрия – составление уравнений совместных перемещений;

(∆ может равняться 0; если ∆≥1,5, то задача статически определимая).

Физика – определение физических соотношений между перемещениями и внутренними силами;

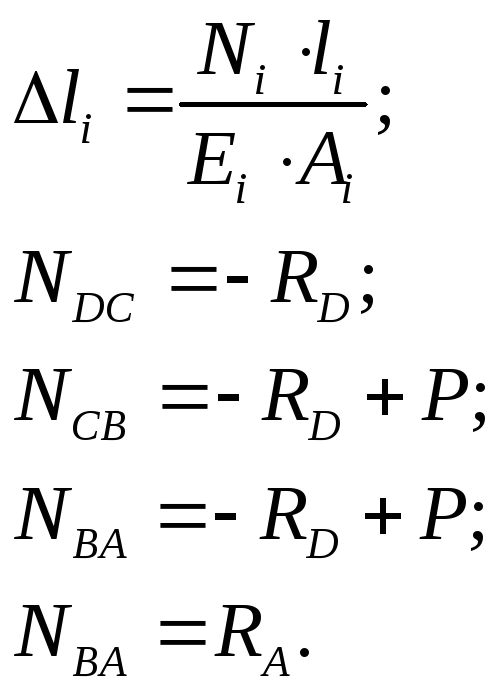
Синтез – совместное решение полученных уравнений.

В уравнение п.2 подставим выражения для ∆l_i по закону Гука.

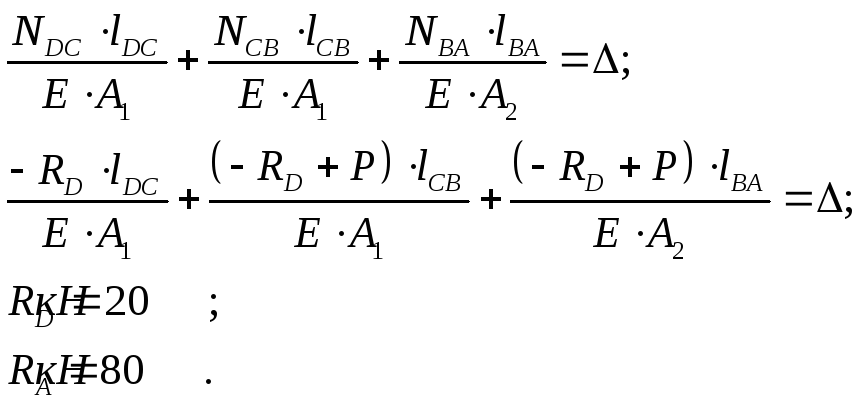Определение внутренних сил:

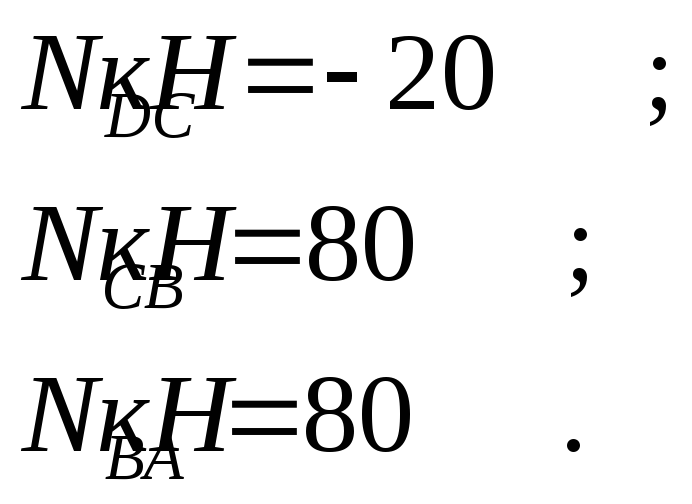
Определение внутренних напряжений:

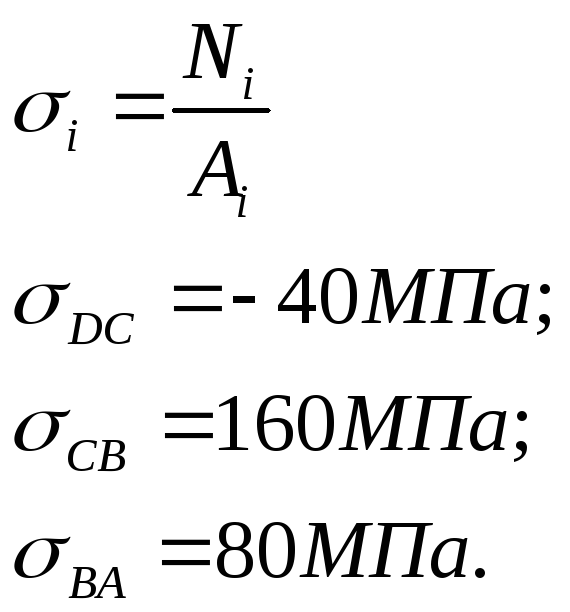
Несмотря на то, что на участке СВ значение напряжений уменьшилось и составило 160МПа, условие прочности все равно не выполняется.

Определение совместных перемещений:

Обобщение:

1В статически неопределимых системах происходит перераспределение внутренних сил, напряжений и перемещений, по сравнению с аналогичными статически определимыми системами.

2Реакции связи а, следовательно, и внутренние силы, в статически неопределимых системах зависят от продольных и поперечных размеров, свойств материала и действия внешних сил.

В статически определенных системах внутренние силы зависят только от внешних сил.

3Меняя жесткость системы подстановкой дополнительных связей, можно добиться рационального распределения внутренних сил при той же величине внешних нагрузок, в связи с этим так же меняются значения напряжений и перемещений.

Б9: Температурные напряжения.

Температурные напряжения

Напряжение в стержне не изменится т.к. при нагревании он изменит свой размер (удлинится).

В стержнях возникает напряжение сжатия.

В статически определимой системе при изменении температуры напряжение не поменяется от действия температуры. Имеет место лишь перенос конструкции (см. рис.1).

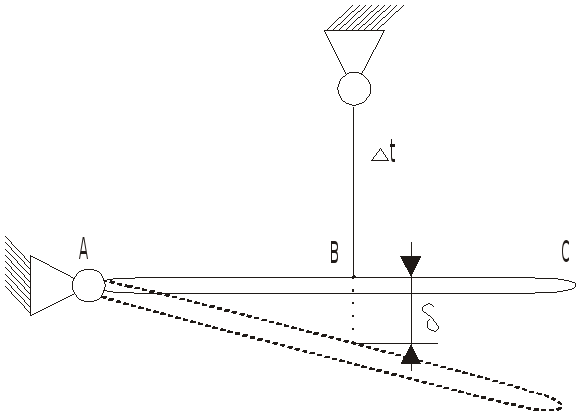
В статически неопределимой системе (см. рис. 2) 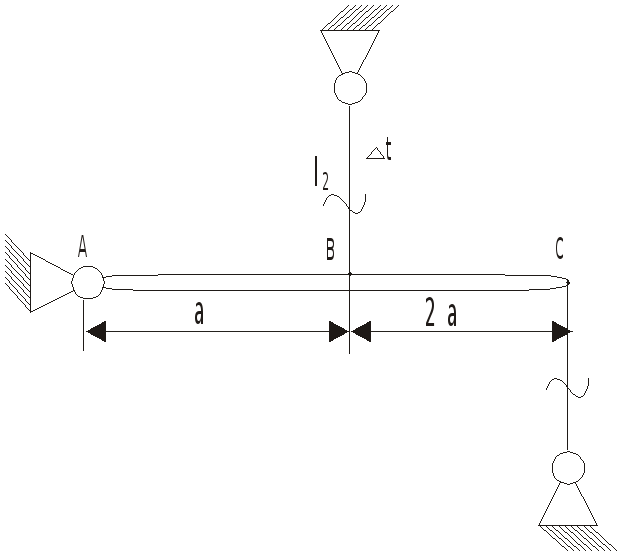стержень не может свободно деформироваться и, как следствие, возникают температурные напряжения. Здесь учитываются не только упругие деформации, но их совместное действие с температурным напряжением.

(α- коэффициент линейного расширения )

Решение задачи, расчетная схема которой приведена на рис. 2.

Статика

Геометрия

Из подобия треугольников АВВ₁ и АСС₁ получаем

Физика

Синтез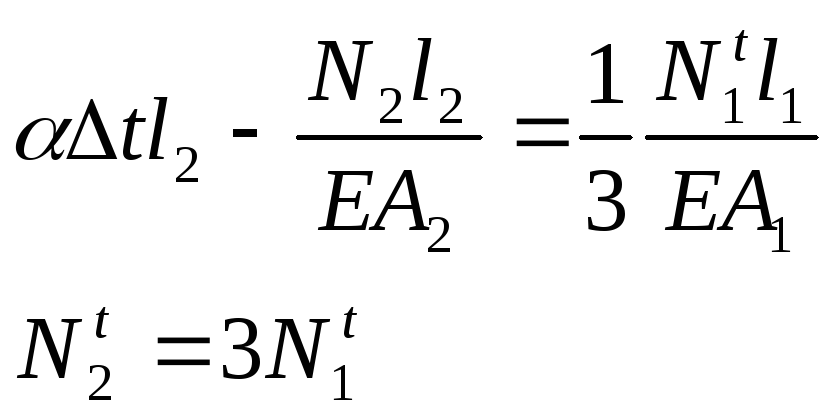

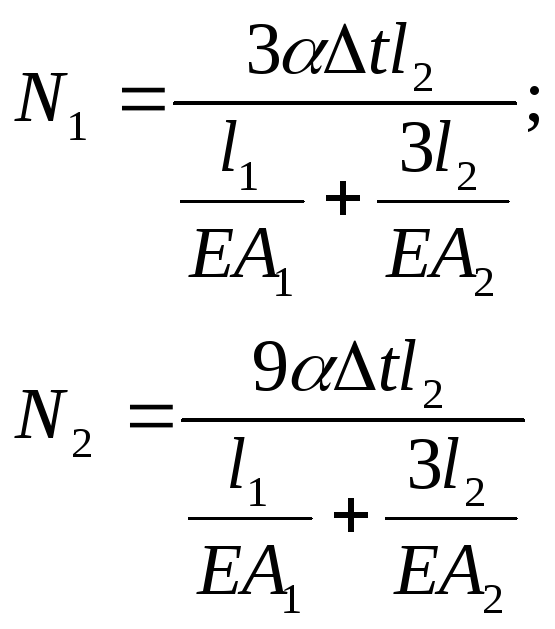
В первом стержне возникает сжимающее напряжение, т.к. балка под действием температуры поворачивается вниз и сжимает этот стержень.

Во втором стержне тоже возникает напряжение сжатия, т.к. полная температурная деформация не может быть реализована из-за сопротивления первого стержня.

Кроме того могут возникать монтажные напряжения.

Совместные действия температурных и внешних нагрузок.

Температурные напряжения при действии внешних нагрузок учитываются со своим знаком и могут как повысить так и понизить его.

1.Статика 2.Геометрия (см. прошлую задачу)

3. Физика

4.

С учетом совместных действий температурных напряжений и напряжений от действия силы Р получаем:

(дополнительно нагружен первый стержень)

В первом стержне напряжение в целом повышается.

Б10: Чистый сдвиг и его особенности. Расчеты на прочность при сдвиговых деформациях.