Нехай на систему з одним ступенем вільності діє сила
Р=Р0+РаСоst (13.4)
Тоді в системі встановлюються коливання з частотою, що збігається з частотою зовнішньої сили
=0+аСоst , (13.5)
де статичні значення
x0=Р011, xа=Раd11, (13.6)
а коефіцієнт зростання амплітуди дорівнює
.
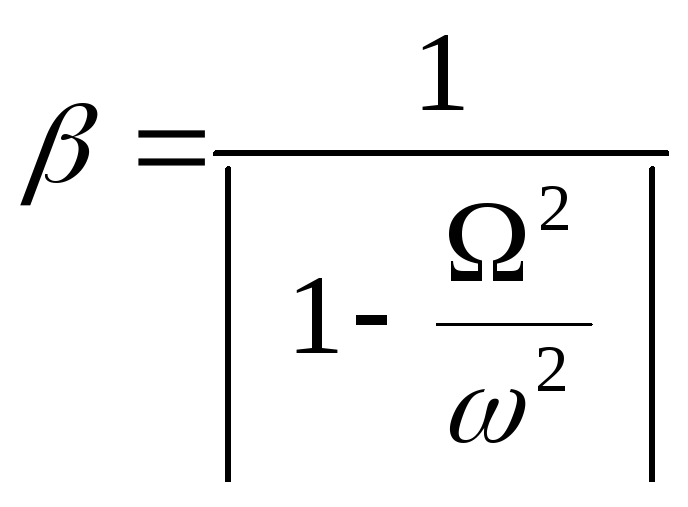(13.7)
Напруження в небезпечному перерізі змінюється також за формулою, аналогічною (13.5). Динамічний коефіцієнт, дорівнює відношенню максимального динамічного напруження до статичного, визначається за формулою
.
(13.8)
Зверніть увагу на явище резонансу, що має місце при співпаданні частоти зовнішнього впливу з власною частотою. Згідно (13.5), (13.7) амплітуда змушених коливань дорівнює нескінченності. При врахуванні сил опору ця величина кінцева, але досить велика. Явище резонансу небезпечно для конструкції. Від нього відбудовуються, підбираючи в такий спосіб параметри конструкції, щоб частота власних коливань відрізнялася від резонансної на 30-40%.
Зауваження: величина амплітуди переміщень складової Ра в (13.4) у випадку виникнення її за рахунок неврівноважених частин двигуна буде залежати від частоти збудження
(13.9)
де РВ - вага неврівноважених деталей,
- эксцентриситет (відстань центра мас до осі обертання), g — прискорення сили ваги.
Формула (13.8) також повинна бути видозмінена
(13.10)
В іншому розрахунок ведеться так само, як і при звичайному силовому впливі.
Питання для самоперевірки
1. Що таке число ступенів вільності?
2. Які коливання називаються вільними?
3. Які коливання називаються вимушеними?
4. Як визначається частота власних коливань системи з одним ступенем вільності?
5. Як визначається період власних коливань?
6. Як знайти амплітуду сталих вимушених коливань?
7. Що таке динамічний коефіцієнт? Як він визначається?
8. У чому заключається явище резонансу?
9. В чому особливість розрахунку систем з неврівноваженими обертаючими деталями?
ПРИКЛАД 16. Посередині прольоту довжиною l = 4 м двотаврової балки на двох опорах (рис. 19) працює двигун вагою Q=25 кН, що робить n0=420 обертів за хвилину. З умови відбудування від резонансу (=1,З) підібрати номер двотавра. Враховуючи те, що вага неврівноважених частин складає 25% від ваги двигуна, визначити допустимий ексцентриситет з умови міцності при [] = 160 Н/мм2 (Е=2.105 Н/мм2).
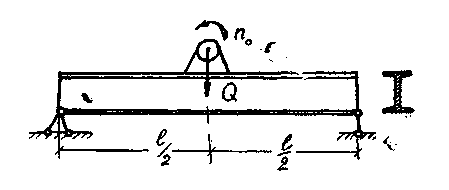
Рис. 19
Розв’язання. Частота вимушених коливань визначається швидкістю обертання двигуна
Тоді
= 1.3 = 57.174 с-1.
Прогин балки посередині прольоту від одиничної сили дорівнює
Відповідно,
Звідки
За ДСТ 8239—72 вибираємо двотавр № 27а, що має
Іх=5500 см4, Wx=407 см3.
Власна частота вибраної системи =56,87 с-1, що складає 1,293 від робочої частоти. Статистичні напруження визначаються за формулою
Додаткові динамічні напруження виникають від сили
.
При врахуванні коефіцієнта зростання амплітуди
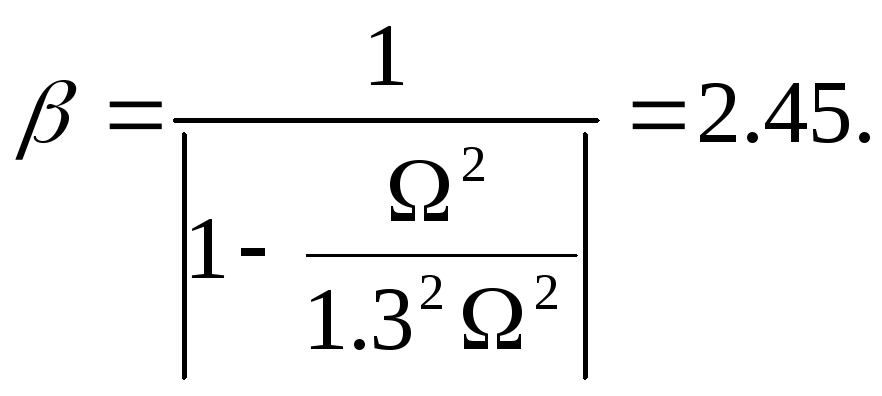
визначимо по формулі
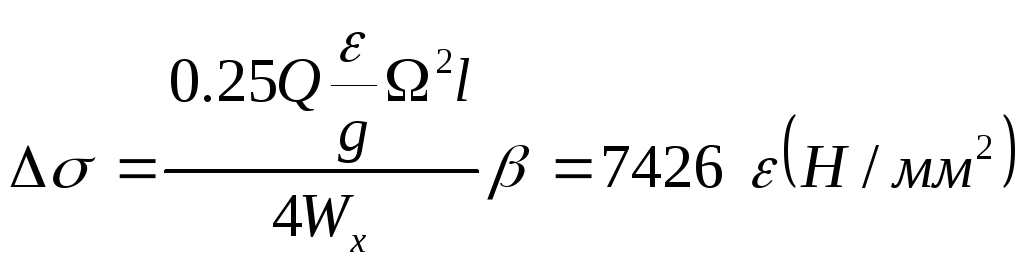
Повне напруження рівне
З умови, що < [], знаходимо
[] < (16-6,14) / 742,6 = 0,0133 (см) = 0,133 (мм).