
- •1.1. Прямые методы решения систем линейных алгебраических уравнений. Метод Гаусса (вычислительная сложность, выбор ведущего элемента).
- •1.2. Понятие об одношаговых и многошаговых методах. Метод Эйлера решения задачи Коши для системы оду первого порядка.
- •2.1. Lu представление матрицы. Обращение матриц и вычисление определителя.
- •2.2. Локальная и глобальная ошибка одношагового метода решения задачи Коши. Задача для погрешности метода, устойчивость и сходимость.
- •3.1. Нормы векторов и матриц. Понятие согласованности и подчиненности матричных норм
- •3.2. Методы Рунге-Кутта. Схема метода четвертого порядка.
- •Число обусловленности матрицы системы лау. Оценки вычислительной погрешности при решении систем лау
- •Многошаговые методы. Явные и неявные методы. Метод Адамса
- •5.1. Понятие устойчивости численных методов для жестких систем. Метод Гира.
- •5.2. Итерационные методы решения систем лау. Метод простой итерации. Условия сходимости и критерий остановки итераций.
- •6.2. Разностная аппроксимация дифференциальных операторов. Сеточный шаблон. Явные и неявные схемы для нестационарных задач математической физики.
- •7.1. Прямые методы вычисления собственных значений. Преобразования подобия. Метод Данилевского.
- •7.2. Порядок аппроксимации разностной схемы. Оценка порядка аппроксимации разностной схемы с весами для нестационарного уравнения теплопроводности.
- •8.1. Оптимальное значение итерационного параметра. Метод минимальных невязок.
- •8.2. Основные понятия теории разностных схем. Пространство сеточных функций и сеточные нормы.
- •9.1. Итерационные методы решения проблемы собственных значений. Степенной метод.
- •9.2. Спектральный метод исследования устойчивости разностных схем для уравнений с постоянными коэффициентами.
- •10.1. Итерационные методы решения нелинейных уравнений. Метод Ньютона.
- •10.2. Устойчивость и сходимость разностных схем. Оценка погрешности разностного решения.
- •21.1. Спектр собственных значений разностного оператора второй производной.
- •21.2. Разностные аналоги формул Грина и теоремы вложения норм сеточных функций.
5.2. Итерационные методы решения систем лау. Метод простой итерации. Условия сходимости и критерий остановки итераций.
Общая
схема больш-ва итерационных методов
реш-я СЛАУ
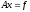 (1)
с невырожденной матрицей
(1)
с невырожденной матрицей
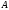 и заданным вектором пр. части
и заданным вектором пр. части
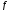 имеет вид
имеет вид
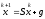 ,
,
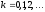 (2)
(2)
где
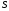 –
матрица итерационного метода,
–
матрица итерационного метода,
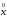 – начальное приближение итерационного
процесса. Последоват-ть
– начальное приближение итерационного
процесса. Последоват-ть
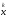 ,
,
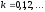 - итерационные приближения
искомого решения.
- итерационные приближения
искомого решения.
Итерационный метод, в котором для
вычисления каждого нового
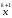 используется лишь
используется лишь
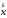 - итерационный методом 1 порядка,
или одношаговым итерационным методом.
- итерационный методом 1 порядка,
или одношаговым итерационным методом.
Итерационный процесс (2) приводит к решению задачи (1) вып-ся условия:
-
последовательность векторов
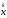 ,
,
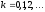 ,
сходится.
,
сходится. -
предел данной последовательности является решением (1).
Из
2 => матрица
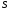 и вектор
и вектор
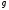 могут
быть заданы в виде:
могут
быть заданы в виде:
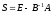 ,
,
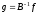 (3)
(3)
где
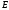 – единичная матрица,
– единичная матрица,
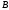 – невырожденная матрица: выполнено
условие 1.
– невырожденная матрица: выполнено
условие 1.
Для произвольных невырожденных
матриц
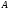 и
и
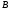 существует единственное значение
вектора
существует единственное значение
вектора
 такое, что
такое, что
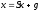 и с учетом выбора (3):
и с учетом выбора (3):
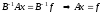
Разнообразие итерационных методов
связано с выбором конкретного вида
матрицы
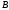 -
переобусловливателя. Если
матрица
-
переобусловливателя. Если
матрица
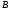 одинакова для всех итераций, то
итерационный процесс называется
стационарным. Среди
нестационарных традиционно
используются переобусловливатели вида
одинакова для всех итераций, то
итерационный процесс называется
стационарным. Среди
нестационарных традиционно
используются переобусловливатели вида
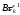 ,
где
,
где
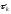 для каждой итерации выбирается из
расчета наибольшей скорости сходимости.
С точки зрения алгоритмической реализации
итерационный процесс (2), (3) удобно
представить в виде
для каждой итерации выбирается из
расчета наибольшей скорости сходимости.
С точки зрения алгоритмической реализации
итерационный процесс (2), (3) удобно
представить в виде
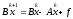 (5)
(5)
При (5), в отличие от (2), (3), не нужен явный
вид м-цы
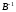 и
выч-е очередного итерационного приближения
сводится к решению СЛАУ:
и
выч-е очередного итерационного приближения
сводится к решению СЛАУ:
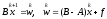 (5')
(5')
Метод
простой итерации: Стационарный
одношаговый итерационный метод вида
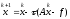 (6). По (2)
(6). По (2)
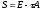 .
По (5)
.
По (5)
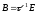 .
.
Теорема.
Пусть
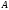 – симметричная положительно определенная
матрица
– симметричная положительно определенная
матрица
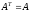 ,
тогда итерационный метод (6) сходится
при
,
тогда итерационный метод (6) сходится
при
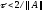 .
.
Доказательство:
Спектральная норма симметричной матрицы
определяется:
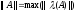 .
Если
.
Если
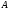 – симметричная матрица, то матрица
– симметричная матрица, то матрица
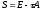 также будет симметричной и
также будет симметричной и
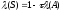 .
Тогда
.
Тогда
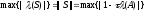 .
Из положительной определенности матрицы
.
Из положительной определенности матрицы
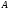 следует, что при
следует, что при
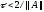 выполняется оценка
выполняется оценка
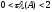 ,
из которой следует, что
,
из которой следует, что
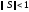 .
.
Теорема.
Пусть
 – симметричная положительно определенная
матрица:
– симметричная положительно определенная
матрица:
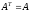 ,
,
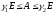 ,
где положит-е постоянные
,
где положит-е постоянные
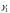 ,
,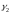 – мин-е и макс-е собственные
значения матрицы
– мин-е и макс-е собственные
значения матрицы
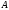 .
Тогда максимальная скорость сходимости
итерационного процесса (6) достигается
при
.
Тогда максимальная скорость сходимости
итерационного процесса (6) достигается
при
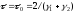 ,
при этом
,
при этом
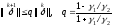 (7)
(7)
Доказательство:
Поиска оптимального зн-я итер-го
параметра
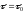 = определение условия минимума
= определение условия минимума
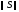 как
функции от
как
функции от .
Найдем явный вид данной функции.
.
Найдем явный вид данной функции.
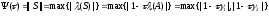 .
.
Несложно
заметить, что
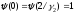 и
и
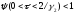 => в интервале значений
=> в интервале значений
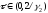 функция
функция
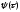 принимает минимальное значение. Поскольку
функция
принимает минимальное значение. Поскольку
функция
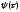 определяется максимальным значением
модулей двух линейных функций, то минимум
такой функции может достигаться только
в точке равенства модулей данных линейных
функций. Ур-е
определяется максимальным значением
модулей двух линейных функций, то минимум
такой функции может достигаться только
в точке равенства модулей данных линейных
функций. Ур-е
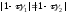 имеет единственный корень на интервале
имеет единственный корень на интервале
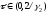 :
:
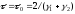 .
При этом
.
При этом
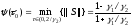 .
Теорема доказана.
.
Теорема доказана.
Скорость
сходимости метода простой итерации
зависит от отношения
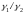 даже в случае оптимального выбора
итерационного параметра. Для симметричных
положительно определенных м-ц
даже в случае оптимального выбора
итерационного параметра. Для симметричных
положительно определенных м-ц
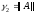 ,
,
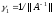 .
=>
.
=>
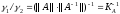 ,
где
,
где
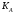 – число обусловленности
– число обусловленности
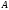 .
Для плохо обусловленных матриц (не
близко к 1) значение
.
Для плохо обусловленных матриц (не
близко к 1) значение
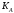 велико, и тогда по (7)
велико, и тогда по (7)
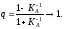 (эфф-ть
м-да может ухудшаться при
(эфф-ть
м-да может ухудшаться при
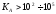 )
)
Вычислительная сложность итерационных методов. Число итераций.
Точное решение задачи неизвестно=>для оценки погрешности текущего итер. приближения используется невязка приближ. реш-я, связанная с ошибкой соотношением:
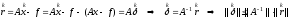 .
.
При
сходимости итер-го процесса норма
погрешности убывает пропорционально
невязке =>в качестве критерия остановки
итераций традиционно используется
условие
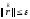 (8)
(8)
Кол-во итераций для достижения заданной точности можно оценить, зная норму матрицы итерационного процесса.
Норма матрицы итерационного процесса
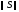 характеризует скорость его сходимости.
Максимальная скорость сходимости
достигается при минимальном значении
характеризует скорость его сходимости.
Максимальная скорость сходимости
достигается при минимальном значении
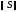 .
.
Можно также использовать переобусловливатель
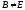 для
уменьшения числа итераций для достижения
заданной точности решения.
для
уменьшения числа итераций для достижения
заданной точности решения.
6.1. Неявные итерационные методы (Зейделя, Якоби, Последовательной верхней релаксации) - стационарные
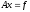 (1)
с невырожденной матрицей
(1)
с невырожденной матрицей
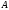
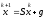 ,
, 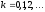 , (2),
где
, (2),
где
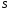 –
матрица итерационного метода,
–
матрица итерационного метода,
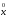 –начальное приближение.
Последовательность
–начальное приближение.
Последовательность
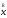 ,
,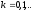 - итерационные приближения решения.
- итерационные приближения решения.
Итерационный процесс (2) приводит к решению (1)
-
последовательность векторов
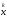 ,
,
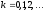 ,
сходится.
,
сходится. -
предел данной последовательности является решением (1).
Из
2 => и вектор
и вектор
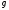 могут
быть заданы в виде:
могут
быть заданы в виде:
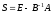 ,
,
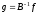 (3)
(3)
где
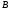 – произвольная невырожденная матрица
(для условия 1).
– произвольная невырожденная матрица
(для условия 1).
В случае плохо обусловленных матриц
(число обусловленности большое, не
стремится к 1) сходимость итерационных
методов вида (2), (3) с оператором
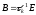 может оказаться очень медленной =>
использование неявных итерационных
методов или итерационных методов с
переобусловливателем.
может оказаться очень медленной =>
использование неявных итерационных
методов или итерационных методов с
переобусловливателем.
Неявный итерационный метод вида
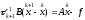 (4) эквивалентен явному итерационному
методу
(4) эквивалентен явному итерационному
методу
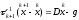 (5), где
(5), где
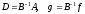 .
.
Основное функциональное назначение
матрицы
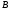 в том, чтобы в итерационных процессах
(4) и (5) достичь существенного уменьшения
числа обусловленности матрицы
в том, чтобы в итерационных процессах
(4) и (5) достичь существенного уменьшения
числа обусловленности матрицы
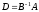 по сравнению с числом обусловленности
исходной матрицы
по сравнению с числом обусловленности
исходной матрицы
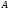 .
.
Второе при выборе переобусловливателя:
возможности вычисления матрицы
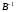 (решения системы
(решения системы
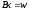 )
намного эффективнее, чем обращение
матрицы
)
намного эффективнее, чем обращение
матрицы
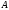 (
(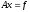 ).
).
Из
функционального назначения идеальным
переобусловливателем является матрица
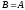 .
Но с точки зрения вычислительной
эффективности выбор оказывается
абсолютно бесполезным, т.к. он возвращает
снова к необходимости решения
.
Но с точки зрения вычислительной
эффективности выбор оказывается
абсолютно бесполезным, т.к. он возвращает
снова к необходимости решения
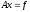 .
.
Метод Якоби.
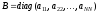 .
В качестве переобусловливателя
используется диагональная матрица,
элементы которой совпадают с диагональными
элементами матрицы
.
В качестве переобусловливателя
используется диагональная матрица,
элементы которой совпадают с диагональными
элементами матрицы
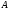 .
Выбор диагонального переобусловливателя
практически не увеличивает вычислительную
сложность отдельной итерации по сравнению
с явным методом. Данный метод может
оказаться полезным для разреженных
матриц с диагональным преобладанием в
случае, когда диагональные элементы
матрицы
.
Выбор диагонального переобусловливателя
практически не увеличивает вычислительную
сложность отдельной итерации по сравнению
с явным методом. Данный метод может
оказаться полезным для разреженных
матриц с диагональным преобладанием в
случае, когда диагональные элементы
матрицы
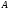 существенно отличаются друг от друга.
Такие матрицы возникают, например, при
дискретизации многомерных уравнений
математической физики с сильно
неоднородными коэффициентами. Если
диагональные элементы матрицы
существенно отличаются друг от друга.
Такие матрицы возникают, например, при
дискретизации многомерных уравнений
математической физики с сильно
неоднородными коэффициентами. Если
диагональные элементы матрицы
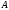 одинаковы (или почти совпадают), то метод
Якоби не имеет преимуществ по сравнению
с явным методом.
одинаковы (или почти совпадают), то метод
Якоби не имеет преимуществ по сравнению
с явным методом.
Метод Зейделя (Гаусса-Зейделя).
Матрица
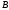 имеет треугольный вид и строится
непосредственно из соответствующих
элементов матрицы
имеет треугольный вид и строится
непосредственно из соответствующих
элементов матрицы
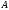 .
В силу треугольности матрицы
.
В силу треугольности матрицы
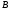 данный метод имеет небольшой рост
вычислительных затрат на одну итерацию
и примерно вдвое (иногда более) сокращает
число итераций для достижения заданной
точности по сравнению с явным методом.
Данный метод практически всегда имеет
положительный эффект по сравнению с
явным методом и Якоби.
данный метод имеет небольшой рост
вычислительных затрат на одну итерацию
и примерно вдвое (иногда более) сокращает
число итераций для достижения заданной
точности по сравнению с явным методом.
Данный метод практически всегда имеет
положительный эффект по сравнению с
явным методом и Якоби.
Метод последовательной верхней
релаксации. В некотором роде
является обобщением метода Зейделя и
метода Якоби. Переобусловливатель
строится из верхней треугольной части
матрицы
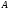 без главной диагонали:
без главной диагонали:
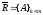 и диагональных элементов матрицы:
и диагональных элементов матрицы:
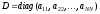 :
:
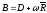 ,
,
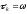 ,
,
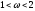
(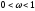 нижняя релаксация, A=A*>0,
нижняя релаксация, A=A*>0,
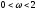 =>
метод релаксации сходится)
=>
метод релаксации сходится)
При
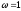 метод последовательной верхней релаксации
совпадает с методом Зейделя, при
метод последовательной верхней релаксации
совпадает с методом Зейделя, при
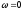 – метод совпадает с методом Якоби.
Оптимальное значение параметра
– метод совпадает с методом Якоби.
Оптимальное значение параметра
 обычно лежит в интервале
обычно лежит в интервале
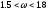 .
В большинстве случаев метод последовательной
верхней релаксации превосходит по
эффективности методы Якоби и Зейделя.
Метод популярен для многомерных задач
математической физики.
.
В большинстве случаев метод последовательной
верхней релаксации превосходит по
эффективности методы Якоби и Зейделя.
Метод популярен для многомерных задач
математической физики.
 -т
модификации данного метода, основанные
на чередовании верхней и нижней
треугольных матриц в
-т
модификации данного метода, основанные
на чередовании верхней и нижней
треугольных матриц в
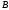 .
.
Для реализации этих трех методов не нужно знания спектра задачи.
