Лабораторна робота №5
“Цілочисельне програмування. Постановка задачі цілочисельного програмування. Метод Гоморі”
(2 години)
Зміст завдання: Розв’язати цідлчисельну задачу лінійного програмування методом Гоморі.
Мета завдання: Навчитися розв’язати цідлчисельні задачі лінійного
програмування методом Гоморі.
1. Постановка задачі.
Порядок виконання:
2. Алгоритм розв’язання задачі.
3. Отримання розв’язку задачі.
4. Аналіз результатів.
Вихідні дані
Для виготовлення трьох видів продукції використовують три види сировини. Запаси сировини, норми витрат та прибуток від реалізації кожного
продукту наведено в таблиці.
|
Типи сировини |
Норми витрат сировини на один виріб |
Запаси сировини |
|||
|
Хліб житній |
Хліб грубого помолу |
Хліб пшеничний |
|
||
|
Дріжджі |
4 |
2 |
1 |
180 |
|
|
Сіль |
3 |
1 |
3 |
210 |
|
|
Домішки харчові |
1 |
2 |
5 |
244 |
|
|
Ціна виробу |
10 |
14 |
12 |
- |
|
Розв‘язати задачу на максимум
Теоретичні відомості
За змістом значної частини економічних задач, що відносяться до задач лінійного програмування, компоненти розв’язку повинні виражатися в цілих
59
числах, тобто бути цілочисловими. До них відносяться, наприклад, задачі, у яких змінні означають кількість одиниць неподільної продукції, число верстатів при завантаженні устаткування, число кораблів, які розподіляють по лініях, число турбін в енергосистемі, число обчислювальних машин у керуючому комплексі і багато іншого.
Задача лінійного цілочислового програмування формулюється так:
знайти такий розв’язок (план) X
(x1 , x 2 ,..., x n ) , при якому лінійна функція
n
Z c j x j
(1)
j 1
приймає максимальне або мінімальне значення при обмеженнях
n
aij x j
i 1
bi , i
1, 2,..., m.
(2)
x j 0, ,
j 1, 2,..., n.
x j цілі числа.
(4)
(3)
Слід зазначити, що класична транспортна задача і деякі інші транспортного типу «автоматично» забезпечують розв’язок задачі в цілих числах (якщо, скінчені цілочислові параметри умов). Однак у загальному випадку умова цілочисловості (4), що додається до звичайних задач лінійного програмування, істотно ускладнює її розв’язок.
Для розв’язку задач лінійного цілочислового програмування використовується ряд методів. Найпростіший з них – звичайний метод лінійного програмування. У випадку, якщо компоненти оптимального розв’язку є нецілочисловими, їх округляють до найближчих цілих чисел. Цей метод застосовують тоді, коли окрема одиниця сукупності складає малу частину всієї сукупності. У іншому випадку округлення може привести до далекого від оптимального цілочислового розв’язку, тому використовують спеціально розроблені методи.
Методи цілочислової оптимізації можна розділити на три основні групи:
а) методи відсікання; б) комбінаторні методи; в) наближені методи. Зупинимося
60
докладніше на методах відсікання.
Методи відсікання. Метод Гоморі
Сутність методів відсікання полягає в тому, що спочатку задача розв’язується без умови цілочисловості. Якщо отриманий план цілочисловий, то задача розв’язана. У іншому випадку до обмежень задачі додається нове обмеження, що володіє наступними властивостями:
воно повинно бути лінійним;
воно повинно відтинати знайдений оптимальний нецілочисловий план;
воно не повинно відтинати жодного цілочислового плану.
Додаткове обмеження, що володіє зазначеними властивостями,
називається правильним відсіканням.
Далі задача вирішується з урахуванням нового обмеження. Після цього в разі потреби додається ще одне обмеження і т.п.
Геометрично додавання кожного лінійного обмеження відповідає проведенню прямої (гіперплощини), що відтинає від багатокутника (багатогранника) розв’язків деяку його частину разом з оптимальною крапкою з нецілими координатами, але не торкається ні однієї з цілих крапок цього багатогранника. У результаті новий багатогранник розв’язку містить усі цілі крапки, які містилися в первинному багатограннику розв’язку і відповідно отриманий при цьому багатограннику оптимальний розв’язок буде цілочисловим. Один з алгоритмів розв’язку задачі лінійного цілочислового програмування (1)-(4), запропонований Гоморі. Цей алгоритм оснований на симплексному методі і використовує досить простий спосіб побудови правильного відсікання.
Нехай задача лінійного програмування (1)-(3) має кінцевий оптимум і на
останньому кроці її розв’язку симплексним методом отримані наступні
рівняння, що виражають основні змінні
x1 , x 2 ,..., x j ,..., x m
через неосновні змінні
x m 1 , x m 2 ,..., x m i ,.., x n
61
оптимального розв’язку
x1
x2
1 1m 1 xm 1
2 2 m 1 xm 1
...
...
1 n xn ,
2 n xn ,
.......................................................................
xi
i i m 1 xm 1
...
i n xn ,
(5)
........................................................................
xm m
m m 1 xm 1
...
m n xn ,
так, що оптимальним розв’язком задачі (1)-(3) є
X 1 2 ,...,
i ,...,
m , 0, 0,..., 0
, у якому, наприклад i – нецілий компонент. У
цьому випадку можна довести, що нерівність1
{ i }
{ i m 1}xm 1
...
{ i n }xn 0,
(6)
яка сформована по i-му рівнянню системи (5), має усі властивості правильного відсікання.
Для розв’язку задачі цілочислового лінійного програмування (1)-(4)
методом Гоморі використовується наступний алгоритм:
1. Симплексним методом вирішити задачу (1)-(3) без враховування умови цілочисловості. Якщо усі компоненти оптимального плану цілі, то він є оптимальним і для задачі цілочислового програмування (1)-(4). Якщо перша задача (1)-(3) нерозв’язувана (тобто не має кінцевого оптимуму або умови її суперечливі), то і друга задача (1)-(4) також нерозв’язувана.
2. Якщо серед компонентів оптимального розв’язку є нецілі значення, то вибрати компоненту з найбільшою цілою частиною і по відповідному рівнянню системи (5) сформувати правильне відсікання (6).
3. Нерівність (6) введенням додаткової невід’ємної цілочислової змінної
перетворити в рівносильне рівняння
{ i }
{ im 1}xm 1
...
{ in }xn
xn 1 ,
(7)
і включити його в систему обмежень (2).
4. Отриману розширену задачу розв’язати симплексним методом. Якщо
62
знайдений оптимальний план буде цілочисловим, то задача цілочислового програмування (1)-(4) розв’язана. У іншому випадку повернутися до п.2 алгоритму.
Якщо задача розв'язувана в цілих числах, то після кінцевого числа кроків
(ітерацій) оптимальний цілочисловий план буде знайдений.
Якщо в процесі розв’язання з'явиться рівняння ( яке виражає основну змінну через неосновні) з нецілим вільним членом і цілими іншими коефіцієнтами, то відповідне рівняння не має розв’язку в цілих числах. У цьому випадку і дана задачі не має цілочислового оптимального розв’язку.
Приклад 1. Для придбання устаткування по сортуванню зерна фермер виділяє 34 грош. од. Устаткування повинне бути розміщене на площі, що не перевищує 60 кв.м. Фермер може замовити устаткування двох видів: менш потужні машини типу А вартістю 3 грош. од., що вимагають виробничу
1 В нерівності (6) присутній символ , який означає дробову частину числа. Цілою частиною числа а називається найбільше ціле число a , яке не
більше
а,
а
дробовою
частиною
числа
є
число
a
,
яке
дорівнює
різниці
між
цим
числом і його цілою частиною, тобто a
a a . Наприклад,
a. для
a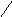
2 13 , a
2, a
2 13 2 13 ;
b. для
a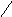
2 13 , a
3 i a
2 13
3 2 .
3
площу 3 кв. м (з урахуванням проходів), і які забезпечують продуктивність за зміну 2 т зерна, і більш потужні машини типу В вартістю 4 грош. од., що займають площу 5 кв. м і забезпечують продуктивність за зміну 3 т сортового зерна.
Потрібно скласти оптимальний план придбання устаткування, що забезпечує максимальну загальну продуктивність за умови, що фермер може
придбати не більш 8 машин типу В.
Р о з в’я з а н н я. Позначимо через
x1 , x 2
кількість машин відповідно типу
А і В, через Z - загальну продуктивність. Тоді математична модель задачі прийме вид:
Z
при обмеженнях:
2x1
3x2
max
63
(1’ )
3x1
|
5x2 |
60, |
(1) |
|
4x2 |
34, |
(2) |
|
x2 |
8, |
(3) |
3x1
x1 0, x2 0,
(2’) (3’)
x1 , x2
цілі числа.
(4’)
Приведемо задачу до канонічного виду, ввівши додаткові додатні змінні
x 3 , x 4 , x 5 . Одержимо систему обмежень:
3x1
3x1
x
2
5x2
4x2
x3 60,
x4 34,
x5 8,
(5’)
x j 0, j
1,2,...,5.
Розв’яжемо задачу симплексним методом.
I крок. Основні змінні
x 3 , x 4 , x 5 ; неосновні змінні
x1 , x 2 .
x3
x4
x
5
60 3x1
34 3x1
8
Z 2x1
5x2 ,
4x2 ,
x2 ,
3x2 .
Перший базисний розв’язок X1
(0; 0; 60;34;8)
– допустимий. Відповідне
значення лінійної функції Z1 0 .
Переводимо в основні змінні змінну
x 2 , що входить у вираз лінійної
функції мети з найбільшим позитивним коефіцієнтом. Знаходимо максимально
можливе значення змінної
x 2 , що «дозволяє» прийняти система обмежень, з
умови мінімуму відповідних співвідношень:
60 34 8
x min ; ; 8,
2 5
4 1
тобто рівняння, що дозволяє (виділене) є третє рівняння. При x 2 8 у
цьому рівнянні x 5
0 , і в неосновні переходить змінна
64
x 5 .
II крок. Основні змінні
x 2 , x 3 , x 4 ; неосновні змінні
x1 , x 5 .
x 2
x 3
x
4
8 x 5 ,
20 3x1
2 3x1
5x 5 ,
4x 5 ,
Z 24
2x1
3x 2 .
X 2 (0;8; 20; 2; 0); Z2
24 . Переводимо в основні змінну
x1 ,
x min
1
; 20 ; 2
2
, а в неосновні x .
3 3 3 4
III крок. Основні змінні
x1 , x 2 , x 3 ; неосновні змінні
x 4 , x 5 .
Після перетворень одержимо:
x 2 1 x
4 x ,
1 3 3 4 3 5
x 2
x
3
Z
8
18
25 1
3
x 4
2
3 x 4
x 5 ,
x 5 ,
1 x .
3 5
X ( 2 ; 8; 18; 0; 0); Z
3 3 3
25 1 .
3
Базисний розв’язок
X 3 оптимальний для задачі (1’)-(3’)
(Z max
Z 25 1 ),
3 3
тому що у виразі лінійної функції відсутні неосновні
змінні з позитивними коефіцієнтами.
Однак розв’язок
X 3 не задовільняє умові цілочислових (4’). По першому
рівнянню зі змінною
x1 , що одержала цілочислове значення в оптимальному
розв’язку (2/3), складаємо додаткове обмеження (6):
2 1 4
0.
x x
3
3 4
3 5
Звертаємо увагу на те, що згідно (5) і (6) беремо дробову частину вільного
65
члена з тим же знаком, що він має в рівнянні, а дробові частини коефіцієнтів
при неосновних змінних x 4 і x 5
– із протилежними знаками.
2 2
,
0
2 1 1 1
0
Тому що дробові частини
3
3 3
3
,
3 3
4 2
3
3
2
2
3 , ту останню нерівність запишемо у виді
2 1 x
3 3 4
2 x 0.
3 5
(6’)
Увівши додаткову цілочислову змінну x 6
нерівності (6.6’) рівняння
0 , одержимо рівносильне
2 1 x
3 3 4
2
3 x5 x6 0.
(7’)
Рівняння (7’) необхідно включити в систему обмежень (5’) вихідної канонічної задачі, після чого повторити процес розв’язання задачі симплексним методом стосовно розширеної задачі. При цьому для скорочення числа кроків (ітерацій) рекомендується вводити додаткове рівняння (7’) у систему, отриману
на останньому кроці розв’язків задачі (без умови цілочисловості).
IV крок. Основні змінні
x1 , x 2 , x 3 , x 6 ; неосновні змінні
x1 , x 2 .
x1
x 2
x 3
2 1 x
3 3 4
8 x 5 ,
18 x 4
2 1
4 x ,
3 5
x 5 ,
2
x 6
3 3 x 4
3 x 5 .
Базисний розв’язок
2
X 4
3
;
8; 18; 0; 0;
2
3
– недопустимий.
(Відмітимо, що після включення в систему обмежень додаткового рівняння, що відповідає правильному відсіканню, завжди буде виходити неприпустимий базисний розв’язок).
Для одержання допустимого базисного розв’язку необхідно перевести в
66
основні змінну, яка входить у рівняння з позитивним коефіцієнтом, у якому
вільний член негативний, тобто x 4
або x 5
(на цьому етапі лінійну функцію
мети не розглядаємо). Переводимо в основні, наприклад, змінну
x 5 .
V крок. Основні змінні
x1 , x 2 , x 3 , x 5 ; неосновні змінні
x 4 ,
x 6 .
Після перетворень одержимо:
x1 2
x2 7
x4
1
2 x4
2x6 ,
3 x ,
2 6
x 19 1 x
3 x ,
3 4 6
2
2
x 1
5
1
2 x4
3
2 x6 ,
Z 25 1 x
4
2
1 x .
2
6
X 5 (2;7;19;0;1;0); Z5
25.
Тому що у виразі лінійної функції мети немає основних змінних з
позитивними коефіцієнтами, то
X 5 – оптимальний розв’язок.
Отже
Zmax 25
при оптимальному цілочисловому розв’язку
X X5
(2; 7;19; 0;1; 0) , тобто максимальну продуктивність 25 т сортового
зерна за зміну можна одержати придбанням 2 машин типу А и 7 машин типу В; при цьому незайнята площа приміщення складе 19 кв. м, залишки коштів з виділених дорівнюють 0, у резерві для покупки 1 машина типу В (шостий компонент змістовного смислу не має).
Контрольні питання:
1. Що таке задача цілочисельного програмування?
2. Які методи розв’язання задач цілочисельного програмування Ви знаєте?
3. Як побудувати додаткове обмеження за методом Гоморі?
4. Наведить алгоритм методу Гоморі.
5. В якому випадку задача не має цілочисельного розв’язку?
67
Лабораторна робота №6 “Транспортна задача. Метод потенціалів.
Постановка задачі, розв’язання задачі симплексним методом в