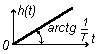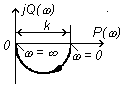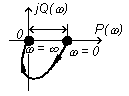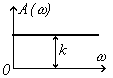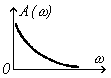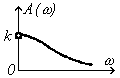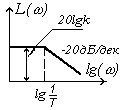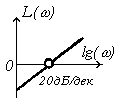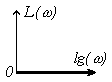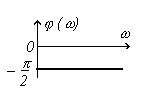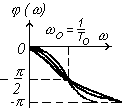3.4. Временные характеристики типовых динамических звеньев

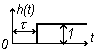
а) Усилительное безынерционное звено.

На основе формул (3.6), (3.7) и (3.30) переходная и импульсная переходная функции: h(t) = = k = const; (3.42)

w(t) = 0. (3.43)

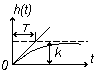
б) Интегрирующее звено.

На основе формул (3.6), (3.7) и (3.31)

h(t) = ; (3.42)

w(t) = = Т_и (3.43)

Графики этих функций показаны на рис. 3.8

Рис.3.8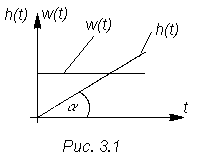

в) Апериодическое звено.

На основе формул (3.6), (3.7) и (3.32)

h(t) = = 1-; (3.44)

w(t) = = . (3.45)

Графики этих функций показаны на рис. 3.9

Рис.3.9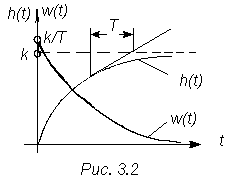

Переходная функция апериодического звена является экспонентой, а поэтому любая подкасательная равна постоянной времени, h(T) = 0,63, h[(35)T]  1.

г) Апериодическое звено второго порядка.

В соответствии с (3.6), (3.7) и (3.35) переходная и импульсная переходная функции инерционного звена второго порядка

h(t) = =1-- ; (3.46)

w(t) = ( - ). (3.47)

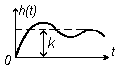
Графики этих функций показаны на рис 3.10.

Рис.3.10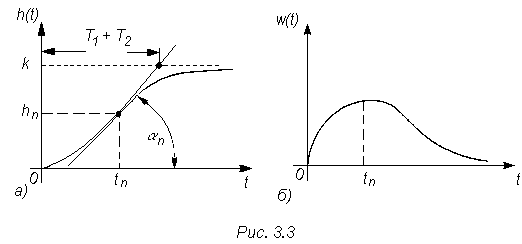

График переходной функции имеет точку перегиба h_n(t_n), что подтверждает наличие двух устройств (элементов), способных накапливать энергию.

Вычислив вторую производную h(t), найдем координаты точки перегиба переходной функции

= = (- + ),

откуда следует, что в точке перегиба

= ,

а поэтому

h_n = h(t_n) = 1-.

Угол наклона касательной к переходной функции, проведенной в точке (t_n,h_n)

tg_n = = w_n(t) = = ,

т.е. касательная в точке перегиба отсекает на асимптоте h(t)=1 отрезок, равный сумме постоянных времени T₁ и T₂ (см. рис 3.10,а).

д.) Колебательное звено

В соответствии с (3.6), (3.7) и (3.35) переходная и импульсная переходная функции колебательного звена (0<<1)

h(t)==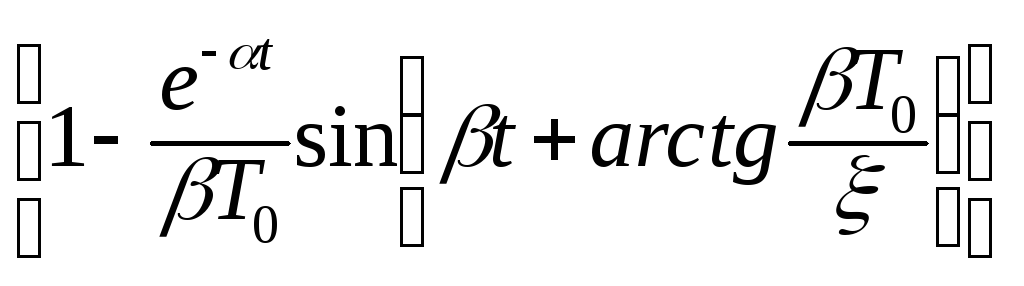; (3.48)

w(t) = . (3.49)

Графики этих функций показаны на рис. 3.11.

Рис.3.11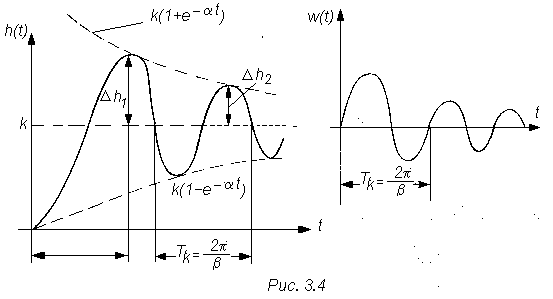

Обратим внимание, что период (затухающих) колебаний

,

где  - частота этих колебаний. Интенсивность затухания колебаний определяется абсолютным значением отрицательной действительной части корней характеристического уравнения. Затухание колебаний за период, как видно из рис.3.11 и выражения (3.48),

,

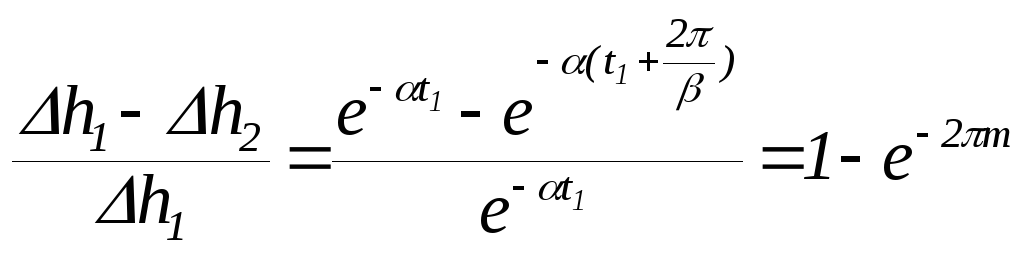где m= - степень затухания колебаний, что соответствует физической сущности динамических процессов в колебательном звене.

е) Консервативное звено

В соответствии с (3.48) переходная и импульсная функции консервативного звена

h(t) = = (1- cos ₀t) (3.50)

w(t) = ₀ sin ₀t (3.51)

где ₀=1/T₀ - частота собственных колебаний, совпадающая с частотой вынужденных колебаний, т.е. имеет место резонанс.

ж) Дифференцирующее звено

В соответствии с (3.39) и (3.40) переходные функции дифференцирующих звеньев определяются следующими формулами:

для идеального дифференцирующего звена

h(t) = Т_д(t) = ; (3.52)

для реального дифференцирующего звена (совпадает с импульсной переходной функцией апериодического звена)

h(t) = = , (3.53)

т.е. при t = 0 h(0) = 1.

Импульсная переходная функция реального дифференцирующего звена

w(t) = (t) - . (3.54)

3.5. Частотные характеристики типовых динамических звеньев

Полученные ранее формулы (3.19), (3.20) и (3.21) являются определяющими для нахождения аналитических выражений для частотных характеристик.

Апериодическое звено

W(j) = = = - j, (3.55)

т.е. U() = ; V() = .

A() = = ; (3.56)

() = arctg = - arctg T. (3.57)

АЧХ и ФЧХ звенья показаны на рис. 3.12.

Рис.3.12

Из рис. 3.12 следует, что апериодическое звено обладает свойством фильтра высоких частот и при изменении частоты от 0 до  сдвиг по фазе изменяется от 0 до -90.

Если АЧХ и ФЧХ этого звена сняты экспериментально, то на частоте =1/Т, A(1/T)=, (1/T)=-45. Поэтому значения эти легко найти. Следовательно, по полученным характеристикам можно найти пара­метры звена (К и Т).

АФХ может быть построена по формуле (3.55) при изменении частоты от 0 до . Это обусловлено тем, что для частотных характеристик линейных звеньев и систем

U(-)=U(), V(-)=-V().

Рис.3.13

Это значит, что АФХ симметрична относительно действительной оси в диапазонах частот от 0 до + и от - до 0.

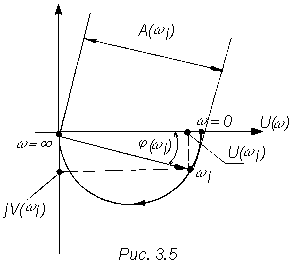
АФХ апериодического звена показана на рис.3.13.

Отметим, что для линейных систем и звеньев строятся асимптотические ЛАЧХ. Рассмотрим методику этого построения для апериодического звена.

Используя выражение (3.56), найдем соотношение для ЛАЧХ в децибелах (дБ).

L()=20lg=20lg1-20lg. (3.58)

Найдем асимптотическое представление для (3.58). Для этого рассмотрим два диапазона частот.

Для 0    1/T L()  20lg1. (3.59)

Для 1/T     L()  20lg1 - 20lgT=-20lgT. (3.60)

Выражения (3.59) и (3.60) представляет собой уравнения прямых линий (асимптот точной ЛАЧХ). Низкочастотная асимптота (3.59) горизонтальна и совпадает с осью частот, а высокочастотная асимптота (3.60) является наклонной прямой линией. Эти асимптоты сопрягаются (соединяются) на частоте сопряжения.

Выясним, с каким наклоном на плоскости ЛАЧХ проводится асимптота (3.60). Для этого найдем изменение ординаты этой асимптоты при десятикратном изменении частоты, т.е. найдем наклон прямой в размерности дБ/дек:

L(10) - L() = 20lg1 - 20lg(10T) - 20lg1 - 20lgT = -20lg 10 = -20 дБ,

а это означает, что наклон этой асимптоты равен -20 дБ/дек.

Максимальная погрешность аппроксимации имеет место при _сопр=1/Т и равна 20lg 3 дБ.

ЛЧХ апериодического звена построены на рис. 3.14.

Рис.3.14

Для интегрирующего звена

W(j) = = ,

т.е. A()= и )=-/2, что отображено на рис. 3.14.

Обратим внимание на то, что интегрирующее звено дает постоянный сдвиг по фазе, равный -90 при всех значениях частот.

ЛАЧХ определяется выражением

-20lg A() = 20lg = 20lg1 - 20lg . (3.61)

Выражение (3.61) - уравнение прямой линии, имеющей наклон -20 дБ/дек на плоскости ЛАЧХ при всех значениях частот. Эта линия проходит при =1с^-1 через ординату L()=0 дБ (см. рис. 3.14)

ЛЧХ других типовых динамических звеньев приведены в таблице 3.1.

Таблица 3.1.

Характеристика основных элементарных звеньев

	Тип звена
Характе ристика	Пропорциональное (усилительное, безынерционное)	Интегрирующее	Апериодическое (инерционное)	Колебательное	Идеальное диф­ференцирующее звено	Запаздывающее
Уравнение	xвых = k xвх, где k - коэффициент усиления или передачи звена	, где Т - постоянная времени	где k -коэффициент передачи звена, Т - постоянная времени	где Т0 ,Т -постоянные времени, k – ко-эффициент передачи	, где Т - постоянная времени	xвых(t - )= xвх,(t), где  - время запаз-дывания
Передаточная функция W(p)	k				T p
Переходная характерис-тика h(t)

Продолжение табл. 3.1.

	Тип звена
Характе-ристика	Пропорциональное (усилительное, безынерционное)	Интегрирующее	Апериодическое (инерционное)	Колебательное	Идеальное диф-ференцирующее звено	Запаздывающее
ЛАЧХ L()
ФЧХ ()