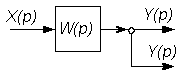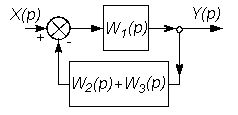2.3. Структурные схемы линейных сау и их преобразование

Из раздела 2.2, следует, что графическое отображение уравнений САУ представляет собой определенные схемы,. которые называются структурными схемами.

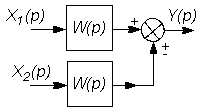
На этих схемах звенья изображаются прямоугольниками, внутри которых записываются передаточные функции. Звенья соединяются линиями, на которых стрелками указывается направление передачи сигнала. На структурных схемах в точках суммирования сигналов изображаются сумматоры, а в точках разветвления сигнала без изменения их величины - узлы (см. рис. 2.3 и 2.4).

Преобразование структурной схемы производится только с целью приведения ее к виду, позволяющему найти необходимые передаточные функции замкнутого контура.

Преобразование структурных схем основано на следующем принципе:

входная и выходная величины преобразуемого участка структурной схемы должны остаться неизменными, так как при соблюдении этого условия исходная и преобразованная структурные схемы являются эквивалентными.

В таблице 2.1 приведены основные правила структурных преобразований.

Таблица 2.1.

Некоторые структурные преобразования

№ п/п	Исходная часть структурной схемы	Преобразованная часть структурной схемы
1
2
3
4
5
6
7
8
9
10

3. Характеристики линейных звеньев и систем

Для анализа линейных звеньев и систем используются временные и частотные характеристики.

3.1. Временные характеристики

Временной характеристикой линейного звена или системы называется вынужденная реакция при нулевых начальных условиях, обусловленная типовым воздействием.

Следовательно, временные характеристики при прочих равных условиях зависят от вида типового воздействия. В ТАУ наиболее часто используется два вида типовых воздействий, подаваемых на вход звена или системы.

Единичная ступенчатая функция

(3.1)

График этой функции показан на рис.

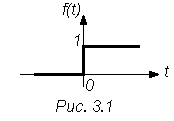
Ступенчатая функция

Изображение по Лапласу ступенчатой функции

(3.2)

Дельта-функция (единичный импульс)

(3.3)

Формула (3.3), определяющая эту функцию, показывает, что идеальное импульсное воздействие, представляет собой бесконечно узкий импульс, при этом

(3.4)

поэтому в ТАУ используется термин “единичный импульс”.

Сопоставляя соотношения (3.1) и (3.2), можно сделать вывод, что

(3.5)

Поэтому на основании формулы (3.2) можно записать

Вынужденная реакция линейного звена или системы на воздействие вида единичной ступенчатой функции называется переходной функцией и обозначается h(t).

, (3.6)

где W(p) - передаточная функция линейного звена или системы.

Вынужденная реакция линейного звена или системы на воздействие вида дельта-функции называется импульсной переходной функцией (весовой функцией) и обозначается w(t).

. (3.7)

Изображение по Лапласу импульсной переходной функции равно передаточной функции, и в этом важность этой временной характеристики. Действительно, изображение по Лапласу линейной системы на воздействие f(t)

X(p)=W(p) F(p), (3.8)

во временной области в силу свойств этого преобразования определяется интегралом свертки

, (3.9)

т.е. вынужденная реакция линейного звена или системы в любой текущий момент времени t на воздействие в момент времени  учитывается с весовым коэффициентом w(t - ).Поэтому w(t) часто называют весовой функцией. Иногда эту функцию обозначают через k(t).