1.11 Анализ устойчивости цифровых систем.

Критерий устойчивости Джури

Необходимым и достаточным условием устойчивости систем

является нахождение всех полюсов передаточной функции замкнутой системы внутри единичного круга на комплексной плоскости, что соответствует условию

где - полюсы передаточной функции замкнутой системы или корни характеристического уравнения.

В настоящее время нет принципиальных трудностей вычисления корней характеристического уравнения с использованием ЭЦВМ, однако при необходимости экономить машинное время целесообразно пользоваться критериями устойчивости Джури, который заключается в следующем.

Пусть задан характеристический полином,

. (1.63)

Введём понятие обратного полинома, получаемого путём перестановки коэффициентов исходного в обратном порядке.

. (1.64)

Разделим на обратный ему. В итоге получим частное от деления число и остаток - полином степени.

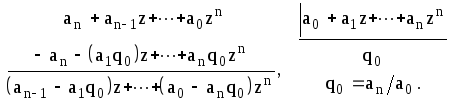
Домножая полученный результат , получаем

Затем делим остаток на обратный ему и определяем новое и

и т.д.

Выполняя деление полиномов на обратные или , получаем последовательность

Необходимым и достаточным условием устойчивости цифровой системы являются неравенства:

(1.65)

Рассмотрим на примере реализацию критерия Джури. Пусть дан характеристический многочлен вида:

Проверим выполнение необходимых условий устойчивости.

Поскольку эти легко вычисляемые неравенства удовлетворяются, то имеет смысл вычислять коэффициент .

Составим обратный полином путём перестановки коэффициентов в обратном примере.

Разделим на

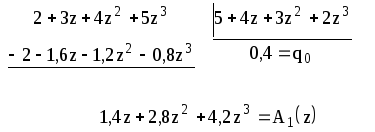
Умножив его на получаем:

Делим на

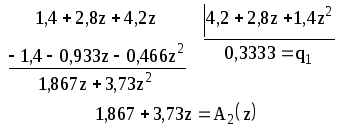
Результаты расчёта показывают, что и по модулю меньше единицы. Таким образом все три неравенства выполняются, следовательно цифровая система устойчива.

Существуют и другие алгоритмы анализа устойчивости цифровых систем, например Кларка и Шура-Кона. Алгоритм Кларка, кроме проверки выполнения первых двух неравенств Джури, включает формирование так называемых "внутренних матриц" и вычисление их определителей. Этот алгоритм эффективен для исследования устойчивости линейных цифровых систем высокого порядка.

Алгебраический критерий Шура-Кона подобен критерию Гурвица для непрерывных систем, для чего составляется специальная матрица из коэффициентов характеристического уравнения и проверяется знак определителя этой матрицы.

Частотный анализ линейных цифровых САУ.

Пусть на входе линейной САУ действует решётчатая функция, представляющая синусоидальную последовательность

(1.66)

где - амплитуда и начальная фаза;

- период дискретности;

- период синусоидальной последовательности.

Найдем реакцию разомкнутой цифровой САУ на синусоидальную последовательность (1.66). Предположим, что канал управления в разомкнутом состоянии устойчив. Поскольку в установившемся режиме устойчивой САУ вынужденная составляющая переходного процесса находится в форме возмущающего воздействия, то выходную последовательность можно представить так:

(1.67)

где - амплитуда на выходе; - сдвиг по фазе.

Для различных значений частоты  можно построить характеристики .

Если известна дискретная передаточная функция , то для получения комплексного спектра, называемого частотной передаточной функцией, необходимо произвести замену

Частотная передаточная функция может быть представлена в показательной и алгебраической форме

(1.68)

где - частотная характеристика линейной цифровой системы,

- фазочастотная характеристика.

Поскольку , то (1.68) является периодической функцией с периодом . Поэтому АФЧХ полностью определяется значениями в диапазоне частот Поскольку действительная часть есть четная функция, то диапазон частот можно уменьшить в два раза, т.е. принять .

В отличие от АФХ и ЛЧХ для обычных систем, передаточные функции которых являются дробно-рациональными, не является дробно-рациональной.

Введем комплексную величину , связанную с комплексной величиной билинейными преобразованиями:

(1.69)

Подставив в это выражение, получим:

(1.70)

где - относительная псевдочастота.

При изменении частоты переменная  принимает значения , т.е. образом единичной окружности в плоскости  является мнимая ось.

Часто вводится понятие абсолютной псевдочастоты

(1.71)

При изменении частоты в диапазоне , абсолютная псевдочастота изменяется в диапазоне . При малых значениях и псевдочастота . Поэтому, выполняя условия , можно в расчетах заменить псевдочастоту  реальной круговой частотой .

Из билинейного преобразования следует, что внутренность единичного круга плоскости отображается на левую полуплоскость переменной .

Располагая частотными характеристиками линейных цифровых систем, можно оценивать их устойчивость, точность и качество. Известен частотный критерий Найквиста, позволяющий судить об устойчивости замкнутой системы по частотной характеристике разомкнутой цифровой системы.

Для того, чтобы замкнутая цифровая система была устойчива, необходимо и достаточно, чтобы годограф при изменении последовательно обходил точку комплексной плоскости в положительном направлении раз, где - число корней характеристического уравнения разомкнутой САУ, лежащих за пределами единичного круга.

Для устойчивой САУ в разомкнутом состоянии , поэтому не должен охватывать точку при изменении . Устойчивость разомкнутой САУ определяется устойчивостью программы управления ЭВМ и устойчивостью приведенной непрерывной части.

При оценке устойчивости цифровой системы с применением ЭВМ необходимо найти точки пересечения годографа частотной характеристики с отрезком действительной оси и оценить алгебраическую сумму числа переходов годографа через этот отрезок.

Переход считается положительным, если он происходит против часовой стрелки, и отрицательный, если по часовой стрелке. Переходы могут принимать значения , если в точке перехода ни и не , и , если или . Частотная характеристика начинается или заканчивается на отрезке .

Частотные характеристики цифровой системы дают информацию о запасе устойчивости по модулю и фазе, показателя колебательности, ширине полосы пропускания, точности в установившемся режиме.

Значение , соответствующее фазовой характеристике , определяет запас устойчивости системы по модулю. Величина , вычисленная для значения частоты среза , при которой , характеризует запас устойчивости по фазе.

Частотная характеристика цифровой системы по каналу ошибки при изменении задания имеет вид:

(1.72)

При наличии пика частотной характеристики (1.72) в среднечастотном диапазоне процессы в САУ носят слабо затухающий характер и может служить мерой колебательности. Показатель колебательности определяется отношением

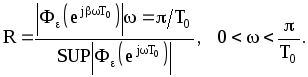
Для астатических систем и большинства статических . Поэтому при оценке запаса устойчивости по величине R можно пользоваться более простым выражением:

(1.73)

Показатель , как и характеризует степень удаления АФХ разомкнутой системы от колебательной границы устойчивости точки . Таким образом показатель колебательности может быть найден как величина наименьшего радиуса окружности, которая касается АФХ разомкнутой системы с центром в точке с координатами , рисунок 1.8.

Приемлемым запасам устойчивости соответствует . Максимальный запас устойчивости по фазе

(1.74)

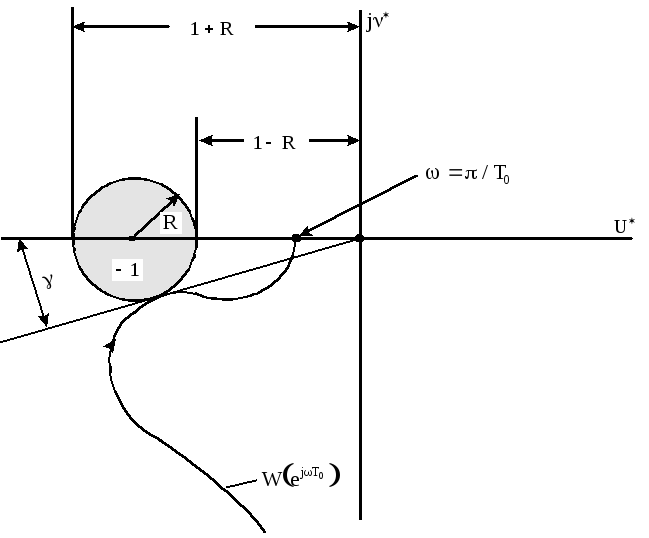
Рисунок 1.8 - Анализ качества цифровых САУ

При выборе параметров системы из требований запаса устойчивости по модулю и фазе появляется неоднозначность из-за двух критериев, поэтому для решения этой задачи на ЭВМ часто применяют однозначный критерий качества , характеризующий расстояние годографа частотной характеристики разомкнутой САУ до точки . Под расстоянием понимается нижняя грань расстояния всех точек годографа до этой точки, т.е.

(1.75)

Для реализации этой процедуры на ЭВМ необходимо рассчитать все точки частотной характеристики, по выражению (1.75) найти из которых следует выбрать минимальное